021. Delete the penultimate node of the linked list

Title:

Given a linked list, delete the penultimate node of the linked list, and return the head node of the linked list.

Example:

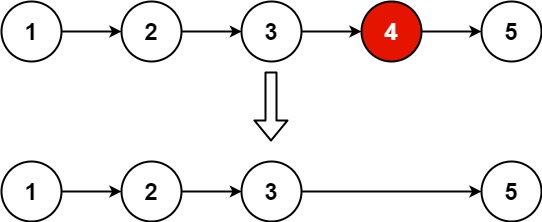
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]

Idea:
Fast and slow pointers: the slow pointer is the head node, the difference between the fast and slow pointers is n, and then when the fast pointer reaches the last node,
The slow pointer just reaches the penultimate node n+1, and then deletes the penultimate node n
Note: add a header node to prevent deleting the header node

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode *dummy = new ListNode(-1);
        dummy->next = head;
        ListNode *slow = dummy;
        ListNode *fast = dummy;
        while(n--) {
            fast = fast->next;
        }
        while(fast != nullptr && fast->next != nullptr) {
            fast = fast->next;
            slow = slow->next;
        }
        slow->next = slow->next->next;
        return dummy->next;
    }
};

022. Entry node of link in linked list

Title:

Given a linked list, return the first node from the linked list into the ring. Starting from the head node of the linked list, the first node entering the ring along the next pointer is the entry node of the ring. If the linked list is acyclic, null is returned.
In order to represent the rings in a given list, we use the integer pos to represent the position where the tail of the list is connected to the list (the index starts from 0). If pos is - 1,
Then there are no links in the linked list. Note that pos is only used to identify the ring and is not passed to the function as an argument.
Note: it is not allowed to modify the given linked list.

Example:

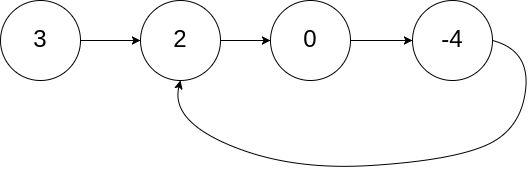
Input: head = [3,2,0,-4], pos = 1
Output: returns the linked list node with index 1
Explanation: there is a ring in the linked list, and its tail is connected to the second node.

Idea:
Method 1: hash table
You can record through the hash table. If you encounter something in the hash table, it is equivalent to the first ring entry

Method 2: speed pointer
a is the length outside the ring, b is the length from the ring inlet to the meeting, and c is the length from the meeting to the ring inlet
a + n * (b + c) + b = 2 * (a + b) distance of first encounter
a = (n - 1) * (b + c) + b;
So fast goes one step at a time, and a will inevitably encounter slow

//Speed pointer
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head;
        ListNode *slow = head;
        while(1) {//First meeting
            //A null pointer is not a loop, return
            if(fast == nullptr || fast->next == nullptr) 
                return nullptr;
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast) break;
        }
        fast = head;
        while(fast != slow) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

023. The first coincident node of two linked lists

Title:

Given the head nodes headA and headB of two single linked lists, please find and return the starting node where the two single linked lists intersect. If two linked lists have no intersection, null is returned.
As shown in the figure, two linked lists intersect at node c1:
The title data ensures that there are no rings in the whole chain structure.
Note that after the function returns the result, the linked list must maintain its original structure.

Example:

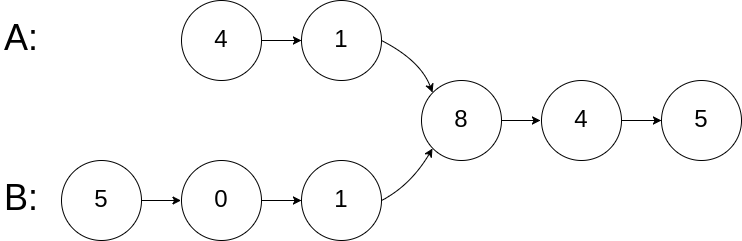
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: the value of intersection node is 8 (note that if two linked lists intersect, it cannot be 0).
Starting from their respective headers, linked list A is [4,1,8,4,5], and linked list B is [5,0,1,8,4,5].
In A, there are 2 nodes before the intersection node; In B, there are 3 nodes before the intersection node.

Idea:
Method 1: hash table
Add a to the hash table and traverse b to determine whether there is a node in the hash table. If there is, it will return, and if there is no, it will not intersect

Method 2: double pointer
a = a + b, b = b + a
If a and b intersect, the intersecting node can be found when traversing the other part

//Double pointer
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if(headA == nullptr || headB == nullptr) return nullptr;
        ListNode *curA = headA;
        ListNode *curB = headB;
        while(curA != curB) {
            curA = curA == nullptr? headB : curA->next;
            curB = curB == nullptr? headA : curB->next;
        }
        return curA;
    }
};

024. Reverse linked list

Title:

For the head node of the order linked list, please reverse the linked list and return the head node of the reversed linked list.

Example:

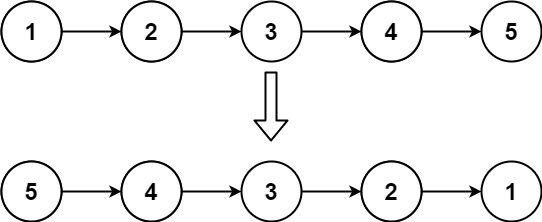
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]

Idea:
Create two double pointers, starting from the head node and the head node and reversing all the time

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *pre = nullptr;
        ListNode *cur = head;
        while(cur != nullptr) {
            ListNode* next = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
};

025. Add two numbers in the linked list

Title:

Two non empty linked lists l1 and l2 are given to represent two non negative integers. The highest digit is at the beginning of the linked list. Each of their nodes stores only one digit. Adding these two numbers will return a new linked list.
It can be assumed that neither number will start with zero except the number 0.

Example:

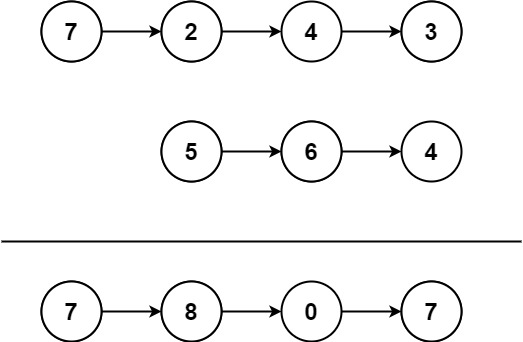
Input: l1 = [7,2,4,3], l2 = [5,6,4]
Output: [7,8,0,7]

Idea:
Method 1: use two stacks (trouble)
First use the two stacks to reverse and add, but finally reverse the linked list

Method 2: flip the linked list
Flip the linked list, add it, and then flip it

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        return reverseList(addList(l1, l2));
    }
    //List addition
    ListNode* addList(ListNode* l1, ListNode* l2) {
        int ans = 0;
        ListNode *node = new ListNode(-1);
        ListNode *dummy = node;
        while(l1 || l2) {
            int x = 0, y = 0;
            if(l1) {
                x = l1->val;
                l1 = l1->next;
            }
            if(l2) {
                y = l2->val;
                l2 = l2->next;
            }
            int num = (x + y + ans) % 10;
            ans = (x + y + ans) / 10;
            node->next = new ListNode(num);
            node = node->next;
        }
        if(ans) {//Carry, plus
            node->next = new ListNode(ans);
            node = node->next;
        }
        return dummy->next;
    }
    //Flip linked list
    ListNode* reverseList(ListNode* head) {
        ListNode *pre = nullptr;
        ListNode *cur = head;
        while(cur) {
            ListNode *next = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
};

026. Rearrange linked list

Title:

Given the head node head of a single linked list L, the single linked list L is expressed as:
L0 → L1 → ... → Ln-1 → Ln
Rearrange them to:
L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → ...
Instead of simply changing the internal value of the node, you need to actually exchange nodes.

Example:

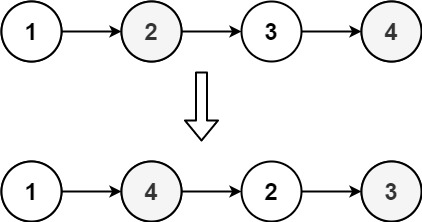
Input: head = [1,2,3,4]
Output: [1,4,2,3]

Idea:
Method 1: linear table
Use the linear table to store, and then use the following table to access the linear table and create a new linked list

Method 2: find the midpoint of the linked list + reverse order of the linked list + merge the linked list

• Find intermediate node reference: 876. Intermediate node of linked list
• Flip the second half of the linked list
• Connect the linked list in turn

//Method 2
class Solution {
public:
    void reorderList(ListNode* head) {
        //Fast and slow pointer to find the midpoint
        ListNode *fast = head;
        ListNode *slow = head;//midpoint
        while(fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        // Flip back half
        fast = nullptr;
        while(slow != nullptr) {
            ListNode *next = slow->next;
            slow->next = fast;
            fast = slow;
            slow = next;
        }
        slow = head;
        //slow is the first half of the linked list, and fast is the second half of the linked list
        while(slow || fast) {
            if(slow) {
                ListNode *next1 = slow->next;
                slow->next = fast;
                slow = next1;
            }
            if(fast) {
                ListNode *next2 = fast->next;
                fast->next = slow;
                fast = next2;
            }
        }
    }
};

027. Palindrome linked list

Title:

Given the head node of a linked list, please judge whether it is a palindrome linked list.
If a linked list is a palindrome, the sequence of linked list nodes is the same from front to back and from back to front.

Example:

Input: head = [1,2,3,3,2,1]
Output: true

Idea:

• Find midpoint
• Flip the second half of the linked list
• Judge whether the front and back parts are palindromes

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        //Find midpoint
        ListNode *fast = head;
        ListNode *slow = head;
        while(fast != nullptr && fast->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        //Flip back half
        fast = reverseList(slow);
        slow = head;//First half
        //Determine whether palindrome
        bool ok = true;
        //Fast < = slow, so fast should be used for while. The following proof:
        //For example: [1,2,1] at this time, slow = 1 - > 2, fast = 1 - > 2, because when 2 flips, the front 1 also points to 2
        //[1,2,2,1] now slow = 1 - > 2 - > 2, fast = 1 - > 2 
        while(ok && fast != nullptr) {
            if(slow->val != fast->val) {
                ok = false;
                break;
            }
            fast = fast->next;
            slow = slow->next;
        }
        return ok;
    }
    //Flip linked list
    ListNode* reverseList(ListNode* head) {
        ListNode *pre = nullptr;
        ListNode *cur = head;
        while(cur) {
            ListNode *next = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
};

028. Flatten multi-level bidirectional linked list

Title:

In the multi-level bidirectional linked list, in addition to the pointer to the next node and the previous node, it also has a sub linked list pointer, which may point to a separate bidirectional linked list. These sub lists > may also have one or more of their own sub items, and so on to generate multi-level data structures, as shown in the following example.
For the head node located at the first level of the list, please flatten the list, that is, flatten such a multi-level two-way linked list into an ordinary two-way linked list, so that all nodes appear in a single-level double linked list.

Example:

Input: head = [1,2,3,4,5,6, null, null, 7,8,9,10, null, null, 11,12]
Output: [1,2,3,7,8,11,12,9,10,4,5,6]
Explanation:

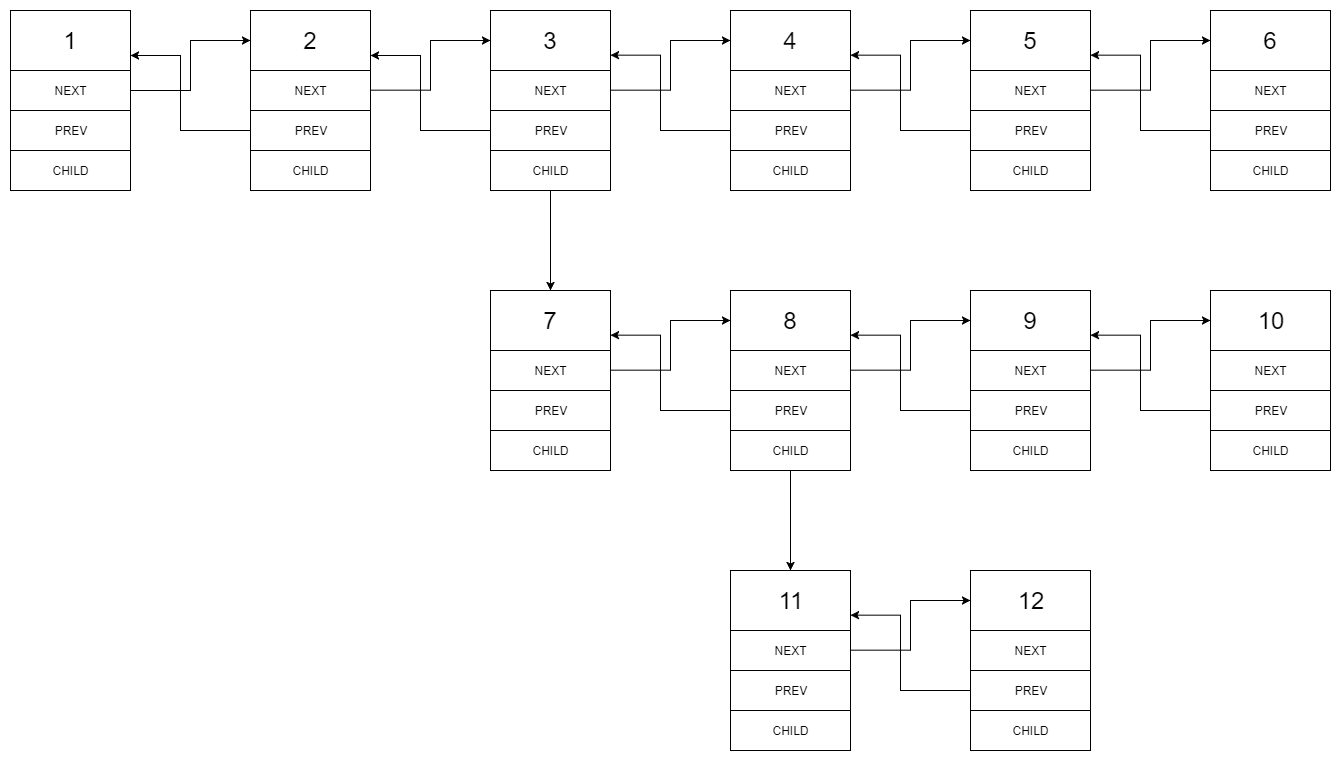
The flattened linked list is shown in the following figure:

Idea:
DFS deep search:
Rotate the picture 90 ° clockwise as a binary tree and traverse it in sequence
Create a new node to connect the front and back nodes during traversal

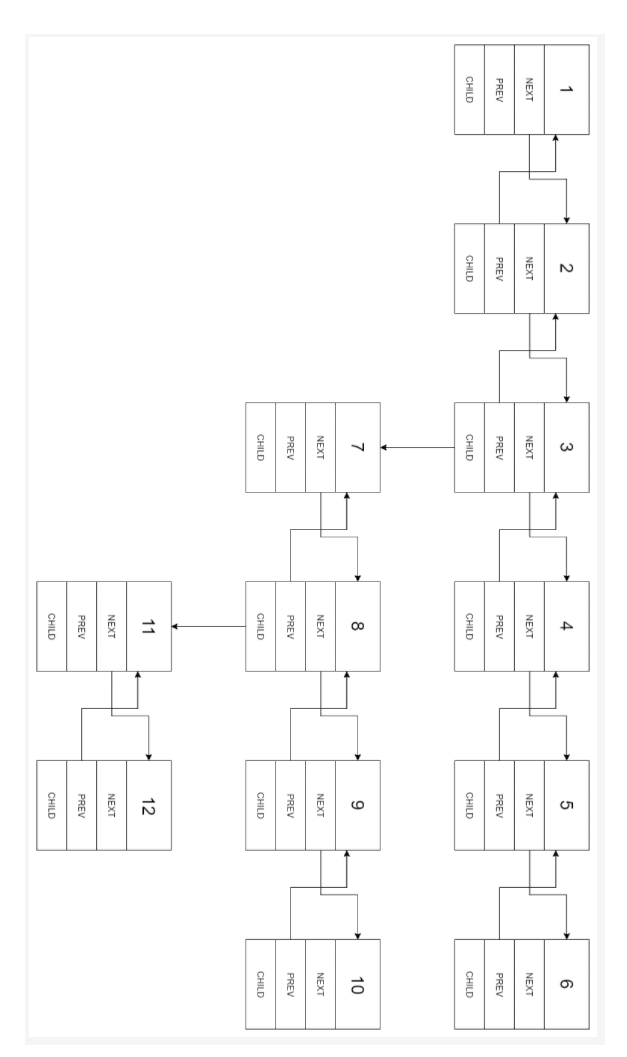
class Solution {
private:
    //Head node
    Node *prevNode = new Node(-1);
public:
    Node* flatten(Node* head) {
        dfs(head);
        if(head != nullptr)
            head->prev = nullptr;
        return head;
    }
    //*The preode follows the dfs traversal, traversing one connection to another
    void dfs(Node* root) {
        if(root == nullptr) return ;
        //cout << root->val;
        Node *left = root->child;
        Node *right = root->next;
        
        prevNode->next = root;
        root->prev = prevNode;
        prevNode = root;

        dfs(left);
        root->child = nullptr;
        dfs(right);
    }
};

029. Sorted circular linked list

Title:

Given a point in a cyclic monotone non decreasing list, write a function to insert a new element insertVal into the list so that the list is still cyclic ascending.
A given can be a pointer to any vertex in the list, not necessarily to the smallest element in the list.
If there are multiple insertion positions that meet the conditions, you can select any position to insert a new value, and the whole list remains orderly after insertion.
If the list is empty (the given node is null), you need to create a circular sequence table and return this node. Otherwise. Please return to the previously given node.

Example:

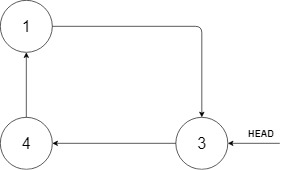
Input: head = [3,4,1], insertVal = 2
Output: [3,4,1,2]
Explanation: in the figure above, there is a circular sequence table containing three elements. You get the pointer of the node with value 3. We need to insert element 2 into the table. The newly inserted node should be between 1 and 3. After insertion, the whole list is shown in the above figure, and finally node 3 is returned.

Idea:
Three situations can be inserted:

• Inserts > = current node, < = next node
• When current node > next node, it indicates the end
  • Maximum number if inserts > = current node
  • If the number of inserts < = next node, it is the decimal point

Exceptions:

• If an empty linked list is inserted directly
• If there is only one element, insert it directly

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        if(head == nullptr) {
            head = new Node(insertVal);
            head->next = head;
            return head;
        }
        Node *cur = head;
        while(cur->next != head) {//Focus, if there is only one number, just skip it
            if((cur->val <= insertVal && insertVal <= cur->next->val) ||
                (cur->val > cur->next->val && insertVal >= cur->val) ||
                (cur->val > cur->next->val && insertVal <= cur->next->val)) {
                break;
            }
            cur = cur->next;
        }
        Node *next = cur->next;
        cur->next = new Node(insertVal);
        cur->next->next = next;
        return head;
    }
};