Word Ladder

The main idea of the topic

Given a starting string and a target string, the starting string is now converted to the target string according to a specific transformation rule, and the minimum number of transformations is determined. The conversion rule is that only one character in a string can be changed at a time, and each converted string must be in a given set of strings.

Solving problems

Reference resources: https://shenjie1993.gitbooks.io/leetcode-python/127%20Word%20Ladder.html
The title was changed in January 2017, so I also changed the code.

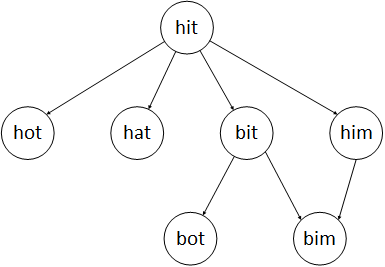
Because each transformed string must be in a given string group, the situation of each change is limited. Now the process of change is made into a tree structure, and the string that is changed from a string becomes a subtree of that string. Referring to the example in the following figure, we can draw the following conclusions:

1. We regard the starting string as the root node. If a node is the target string in the process of change, then we find a change path.

2. The height of the node can reflect several changes when it changes to the node. For example, the hot changes once at the next level of the root node, and the hut and bot change twice at the next level.
Strings that have appeared in the upper layer of the tree need not reappear in the lower layer, because if the string is the intermediate string that must be passed in the conversion process, then the upper string should be selected to continue to change, and its conversion times are less.

3. If there are several strings in the previous layer that can be converted to the same string in the next layer, we only need to find one conversion relationship. For example, bit s and him s in the example can be converted to bim. We just need to know that one relationship can be converted to bim. We don't need to find all the conversion relationships, because it is certain that two transformations can be converted to bim.

4. Based on points 3 and 4, when a string in a collection appears in a tree, it can be deleted from the collection. This prevents the string from being iterated over and over again.

5. At this point, the problem becomes a depth-first traversal problem. It only needs to traverse the nodes of each layer in turn. If the target string is found in that layer, it only needs to return the corresponding number of changes. If the node to a certain level of tree can not continue to extend downward, and the target character is not found.

Code

wordList to set

Otherwise, LTE. Final 668ms

class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        wordSet = set(wordList)
        cur_level = [beginWord]
        next_level = []
        depth = 1
        n = len(beginWord)  # Enlightenment string length
        while cur_level:
            for item in cur_level:
                if item == endWord:
                    return depth
                for i in range(n):
                    for c in 'abcdefghijklmnopqrstuvwxyz':
                        word = item[:i] + c + item[i + 1:]
                        if word in wordSet:
                            wordSet.remove(word)
                            next_level.append(word)
            # The next layer of the tree is created.
            depth += 1
            cur_level = next_level
            next_level = []
        return 0

cur_level is also converted to set

It's supposed to be quicker, but it's not, but after changing next_level.append(word) to next_level. append (str (word), it's up to 500 ms. Not very understanding.
PS: After experimentation, it was found that sometimes it would be worse. It seems that the leetcode time can not be believed.

class Solution(object):
    def ladderLength(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: int
        """
        wordSet = set(wordList)
        cur_level = set([beginWord])
        next_level = set()
        depth = 1
        n = len(beginWord)  # Enlightenment string length
        while cur_level:
            for item in cur_level:
                if item == endWord:
                    return depth
                for i in range(n):
                    for c in 'abcdefghijklmnopqrstuvwxyz':
                        word = item[:i] + c + item[i + 1:]
                        if word in wordSet:
                            print type(word), type(str(word))
                            wordSet.remove(word)
                            next_level.add(str(word))
            # The next layer of the tree is created.
            depth += 1
            cur_level = next_level
            next_level = set()
        return 0

Word Ladder II

The main idea of the topic

Given a starting string and a target string, the starting string is now converted to the target string according to specific transformation rules, and the conversion process with the least number of conversion times is obtained. The conversion rule is that only one character in a string can be changed at a time, and each converted string must be in a given set of strings.

Solving problems

For each transformed string to be in a given string group, each change is limited. Now the process of change is made into a tree structure, and the string that is changed from a string becomes a subtree of that string. Referring to the example in the following figure, we can draw the following conclusions:

1. We regard the starting string as the root node. If a node is the target string in the process of change, then we find a change path.

2. The height of the node can reflect several changes when it changes to the node. For example, the hot changes once at the next level of the root node, and the hut and bot change twice at the next level.

3. There is no need for strings that appear in the upper layer of the tree to reappear in the lower layer, because if the strings are intermediate strings that must be passed in the conversion process, then the strings in the upper layer should be selected to continue to change, and its conversion times are less.

4. If there are several strings in the previous layer that can be converted to the same string in the next layer, we only need to find one conversion relationship. For example, bit s and him s in the example can be converted to bim. We just need to know that there is one relationship that can go to bim. There is no need to find all the conversion relationships, because it is certain that two transformations can be converted to bim.

5. Based on Points 3 and 4, when a string in a collection appears in a tree, it can be deleted from the collection. This prevents the string from being iterated over and over again.

At this point, the problem becomes a depth-first traversal problem, which only needs to traverse the nodes of each layer in turn. If the target string is found in that layer, it only needs to return the corresponding number of changes. If the node to a certain level of tree can not continue to extend downward, and the target character is not found

Code

Change the subject slightly.

class Solution(object):
    def findLadders(self, beginWord, endWord, wordList):
        """
        :type beginWord: str
        :type endWord: str
        :type wordList: List[str]
        :rtype: List[List[str]]
        """
        def bfs(front_level, end_level, is_forward, word_set, path_dic):
            if len(front_level) == 0:
                return False
            if len(front_level) > len(end_level):
                return bfs(end_level, front_level, not is_forward, word_set, path_dic)
            for word in (front_level | end_level):
                word_set.discard(word)
            next_level = set()
            done = False
            while front_level:
                word = front_level.pop()
                for c in 'abcdefghijklmnopqrstuvwxyz':
                    for i in range(len(word)):
                        new_word = word[:i] + c + word[i + 1:]
                        if new_word in end_level:
                            done = True
                            add_path(word, new_word, is_forward, path_dic)
                        else:
                            if new_word in word_set:
                                next_level.add(new_word)
                                add_path(word, new_word, is_forward, path_dic)
            return done or bfs(next_level, end_level, is_forward, word_set, path_dic)

        def add_path(word, new_word, is_forward, path_dic):
            if is_forward:
                path_dic[word] = path_dic.get(word, []) + [new_word]
            else:
                path_dic[new_word] = path_dic.get(new_word, []) + [word]

        def construct_path(word, end_word, path_dic, path, paths):
            if word == end_word:
                paths.append(path)
                return
            if word in path_dic:
                for item in path_dic[word]:
                    construct_path(item, end_word, path_dic, path + [item], paths)


        front_level, end_level = {beginWord}, {endWord}
        path_dic = {}
        wordSet = set(wordList)
        if endWord not in wordSet:
            return []
        bfs(front_level, end_level, True, wordSet, path_dic)
        path, paths = [beginWord], []
        # print path_dic
        construct_path(beginWord, endWord, path_dic, path, paths)
        return paths

summary

The second question is not well read.