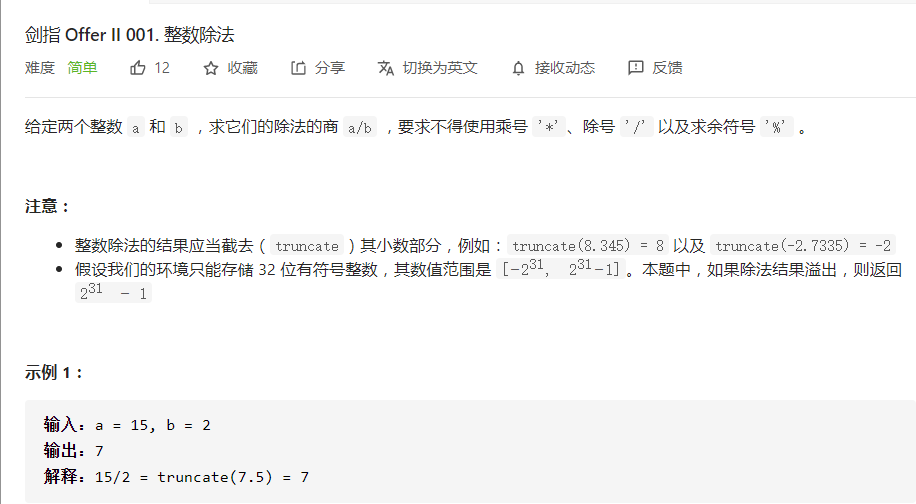
Integer division

thinking

• Cross border problem

  • Critical point negative 0x8000000, positive 07fffff
  • Convert a and b to negative numbers, and the highest bit can be used.
  • The problem becomes a loop, which is a < = B
  • Critical point:
    • a==0 return 0;
    • if ((a == 0x80000000 && b == -1) || (a == 0x7fffffff && b == 1)) return 0x7fffffff;
      if ((a == 0x80000000 && b == 1) || (a == 0x7fffffff && b == -1)) return 0x80000000;

• Subtraction implementation

  • a=a-b, but the operation is too cumbersome. b+b each time; Until b+b < A; The amount of b subtracted is twice the increase.
  • Use two variables temp = temp + temp; Count = count + count 2x increase, similar to shift left
  • In the process, a two-dimensional array vectortc[2] is used to store temp and count, and there is no need to accumulate from scratch next time
  • Temp here is also a negative number out of bounds, so temp > 0xc0000000 should be satisfied;
  • When temp + temp > A is not satisfied with subtraction, the appropriate temp and count will be obtained directly from the vector next time
  • pop operation is required after obtaining. The last one is temp=b, count=1; At most, it won't be smaller.

int divide(int a, int b) {
	if ((a == 0x80000000 && b == -1) || (a == 0x7fffffff && b == 1))  return 0x7fffffff;
	if ((a == 0x80000000 && b == 1) || (a == 0x7fffffff && b == -1))  return 0x80000000;
	if (a == 0) return 0;
	
	bool flag = (b < 0 && a < 0) || (a > 0 && b > 0) ? true : false;
	//Turn negative
	a = a < 0 ? a : 0 - a;
	b = b < 0 ? b : 0 - b;
	
	int div = 0;
	//Record temp and count
	vector<int>tc[2];
	int temp = b;
	int count = 1;
	while (a<=b)
	{
		if (tc[0].empty()) {
			while (temp > 0xc0000000 && temp + temp > a)
			{
				tc[0].push_back(temp);
				tc[1].push_back(count);
				temp = temp + temp;//move
				count = count + count;
			}
		}
		else
		{
			while (temp < a&& !tc[0].empty())
			{
				temp = tc[0].back();
				count = tc[1].back();
				tc[0].pop_back();
				tc[1].pop_back();
			}
		}
		//Same position.
		a = a - temp;
		div = div + count;
	}
	div = flag ? div : 0 - div;
	return div;
}

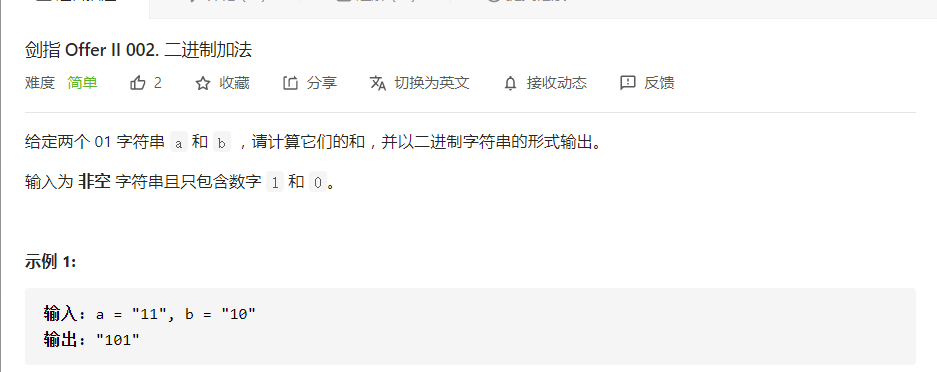
Binary addition

thinking

• The two strings a and B are traversed from the tail and added to the string in reverse order after completion.
• The addition of characters ch=A -'0 '+ B -'0' + C has only one '0', ensuring that '0' < = ch < ='3 '
• If ch > = 2, carry and CH minus 2; If not, modify C to '0'
• One cycle ensures that both a and b can traverse, make a judgment on endA and endB, and then copy [faster, low code repetition rate]
• Finally, judge whether C is' 1 '. If yes, it needs to be added again

string binaryAdd(string a, string b) {
	string add="";
	//XOR from last
	// 0 0 =0 ，0 1= 1，1 0=1,1 1=0==>c[i]=1
	// add flashback insertion. Just reverse the order
	int endA = a.length() - 1;
	int endB = b.length() - 1;
	char C='0';
	char ch;
	while (endA>=0||endB>=0)
	{
		int A = endA >= 0 ? a[endA--] - '0' : 0;
		int B = endB >= 0 ? b[endB--] - '0' : 0;
		ch = A + B + C;
		//cout <<ch<< endl;
		if (ch >= '2') {
			C = '1';
			ch = ch-2;
		}
		else {
			C = '0';
		}
		add += ch;
	}
	//If there is another C at the end, add it directly
	if (C == '1')
		add += '1';
	//A reverse order
	reverse(add.begin(),add.end());
	return add;
}

The number of 1 in the first n binary

thinking

• Whether to carry depends on k-1%2 the situation
• (k-1)%2==0, then the number is the previous + 1
• If not, carry. It can be regarded as (k-1)/2, and the + 1 operation is the next bit of (k-1)/2.

a r r [ i n d e x ] = { a r r [ i n d e x − 1 ] + 1              ( i n d e x − 1 ) % 2 = = 0 a r r [ ( ( i n d e x − 1 ) / 2 ) + 1 ]          ( i n d e x − 1 ) % 2 ! = 0 arr[index]=\left\{ \begin{matrix} arr[index-1]+1 ~~~~~~~~~~~~ (index-1)\%2==0 \\ arr[((index-1)/2)+1] ~~~~~~~~(index-1)\%2 !=0 \end{matrix} \right. arr[index]={arr[index−1]+1            (index−1)%2==0arr[((index−1)/2)+1]        (index−1)%2!=0​

vector<int> countBits(int n) {

	vector<int>arr;
	arr.push_back(0);//0 go in first
	int index = 1;//Start with 1
	while (index<=n)
	{
		if ((index - 1) % 2 == 0)
			arr.push_back(arr[index - 1] + 1);
		else
			arr.push_back(arr[((index - 1) / 2)+ 1]);
		index++;
	}

	for (vector<int>::iterator it = arr.begin(); it != arr.end(); it++) {
		cout << *it << "	";
	}

	return arr;
}

A number that appears only once

Simple sort space complexity O(lgN)

thinking

• Sort first
• Judge whether the ending is a single existence
• The left and right adjacent data of a single existence are different from it

int easySingleNumber(vector<int>& nums) {

   int num=0;
   int len = nums.size() - 1;
   if (len == 0)
   	return nums[0];
   if ((len) % 3 != 0)//Input error
   	return 0;
   sort(nums.begin(), nums.end());

   //The other three are the same. Find the one that is different from the previous one
   //Look at the head and tail first: because there is the possibility of crossing the border
   if (nums[0] != nums[1])
   	return nums[0];
   if (nums[len] != nums[len-1])
   	return nums[len];
   for (int i = 1; i < nums.size()-1; i++) {
   	if (nums[i - 1] != nums[i] && nums[i] != nums[i + 1]) {
   		num = nums[i];
   		break;
   	}
   }
   return num;
}

Bit operation space complexity O(1)

thinking

• If there are three numbers that will be the same, it is proved that their addition% 3 = = 0;
• Integer has 32 bits. Traverse the array and add the bits of each bit. This bit must be bit%3==1 or 0
• Use count to record the bit addition of this bit [current num data = num shift right (31-i) bit & 1]
• If count%3 is 1, the single data bit is 1. Otherwise, it is 0
• Directly obtain the first k bits, and advance the existing (k-1) bits by one + (bit%3= 0)

 int singleNumber(vector<int>& nums) {
	int result=0;//Store results
	for(int i=0;i<32;i++){
		int count=0；
		//Traverse the array to add the bits
		for(auto num:nums){
			count+=(num>>(31-i))&1;
		}
		//Get the first i bit
		result=(result<<1)+(count%3!=0);
	}
	return result;
}