Recently, Beijing is so cool that it rains all the time, refreshing my view of not much rain in Beijing. Just brushed a title labeled "hard", but in fact it is not very difficult. Now let's share our experience with you.

The title is as follows:

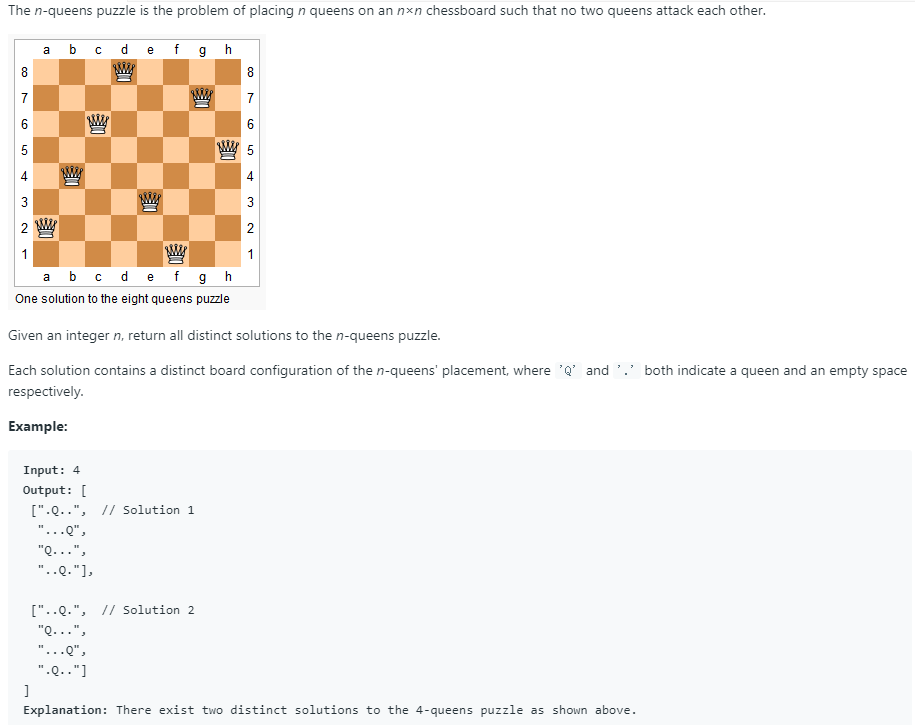
Topic analysis:

This topic is the famous N Queens Problem: Require n queens to be placed in n*n chessboard, so that the horizontal, vertical and two angles of 2*n-1 diagonal direction will not appear two queens at the same time. Please find all solutions to the n Queen problem. In the solution, the queen's position is required to be expressed by'Q', while the non-queen's position is expressed by'.'.

Method 1 (Recursive Backtracking)

Using the "trial-and-error method", first record the queen's current line with index, then record a solution of the n-queen problem with row. Use the Boolean array col, diam1 and diam2 to mark whether the queen has been placed in the longitudinal and diagonal directions of two angles respectively. The number of diagonals of two angles is 2*n-1, and the diagonals from the upper right to the lower left satisfy the sum of the horizontal and vertical coordinates, and the diagonals from the upper left to the lower are fixed values. The diagonal line at the lower right satisfies the abscissa-ordinate value. Then the findsolvenquens function is created to make a recursive call, where the recursive termination condition is "if (index = = n) res.push back (getResult (n, row));". When the longitudinal direction of the access position and the diagonal direction of both angles do not let the queen go, then the queen can be put down at this position and continue the recursive call. Since backtracking is required here, the previous markup needs to be cleared. Finally, by using getResult function, each row of the solution of the n-queen problem is transformed into the form of the solution required by the problem, and all the solutions of the n-queen problem are returned.

The solution code is as follows:

class Solution{
private:
    void findsolveNQueens(int n, int index, vector<int>& row, vector<bool>& col, vector<bool>& diam1, vector<bool>& diam2, vector<vector<string>>& res){
        if ( index == n ) res.push_back( getResult( n, row) );

        for (int i = 0; i < n; i++) {
            //Since the array diam2 is accessed from 0, the overall need is + n-1, that is, index-i+n-1.
            if( !col[i] && !diam1[index+i] && !diam2[index-i+n-1] )
                {
                    row.push_back(i);
                    col[i] = true;
                    diam1[index+i] = true;
                    diam2[index-i+n-1] = true;
                    findsolveNQueens(n, index+1, row, col, diam1, diam2, res);
                    col[i] = false;
                    diam1[index+i] = false;
                    diam2[index-i+n-1] = false;
                    row.pop_back();
             }
        }
    }

    vector<string> getResult( int n, vector<int>& row ){
        vector<string> result ( n, string(n,'.') );
        for ( int i = 0; i < n; i++ ) {
            result[i][row[i]] = 'Q';
        }
      return result;
    }


public:
    vector<vector<string>> solveNQueens( int n ){
        vector<vector<string>> res;
        vector<int> row;
        vector<bool> col( n, false );
        vector<bool> diam1( 2*n-1, false );
        vector<bool> diam2( 2*n-1, false );
        findsolveNQueens( n, 0, row, col, diam1, diam2 , res);

        return res;
    }
};

The results are as follows:

 

 

 

Over the long term, with the king, a summary of the increase, to be continued.