LeetCode - linked list

Catalog

1. Summary
2. Find the intersection of two linked lists
3. Linked list inversion
4. Merge two ordered lists
5. Remove duplicate nodes from an ordered list
6. Delete the nth last node of the linked list
7. Adjacent nodes in exchange linked list
8. Linked list summation
9. Palindrome linked list
10. Separate list
11. Link list elements gather by parity

0. overview

1. The list is a null node, or has a value and a pointer to the next list, so many list problems can be solved by recursion

1. Find out the intersection of two linked lists

1. Summary
   
   1. Two linked lists a and B intersect at c1, but they will not separate after intersecting, because each node has only one next pointer, so there can only be one successor node

2. way of thinking

1. Let the length of A be a+c, and the length of B be b+c, where c is the length of the common part of the tail. It can be seen that a+c+b = b+c+a
2. When the pointer to the A-linked list accesses the end of the linked list, let it access the b-linked list from the head of the b-linked list; similarly, when the pointer to the b-linked list accesses the end of the linked list, let it access the A-linked list from the head of the A-linked list. In this way, the pointers of two linked lists a and B can access the intersection at the same time
3. If there is no intersection, then a+b=b+a, l1 and l2 are null at the same time, so the loop exits

3. code

public static ListNode getIntersectionNode(ListNode head1, ListNode head2) {
        ListNode l1 = head1;
        ListNode l2 = head2;
        while (l1 != l2) {
            l1 = l1 == null ? head2 : l1.next;
            l2 = l2 == null ? head1 : l2.next;
        }
        return l1;
    }

4. supplement

1. If it is only to judge whether there are intersections, there are two solutions
   1. Connect the end of the first linked list to the beginning of the second linked list to see if there is a link in the second linked list
   2. Or directly compare whether the last node of two linked lists is the same

2. List reversal

1. recursive version

1. thinking
   1. Set the head node as head and the next node as next.
   2. Through recursion reverseList(next), you can go to the next to last node head and tail node next.
   3. Point next.next to the previous node head, and then set head.next to null. Reverse from back to front
2. Code

2. head insertion

1. thinking
   I don't quite understand
2. Code

public static ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode next = head.next;
        ListNode newHead = reverseList(next);
        next.next = head;
        head.next = null;
        return newHead;
    }

    public static ListNode reverseList2(ListNode head) {
        ListNode newHead = new ListNode(-1);
        while (head != null) {
            ListNode next = head.next;
            head.next = newHead.next;
            newHead.next = head;
            head = next;
        }
        return newHead.next;
    }

3. Merge two ordered lists

1. thinking
   1. If l1 or l2 is null at the beginning, there is no need to merge any operations, so we only need to return non empty linked list.
   2. Otherwise, it is necessary to determine which header element of l1 and l2 is smaller, and then recursively determine the next value added to the result.
   3. If both linked lists are empty, the process will terminate, so the recursive process will eventually terminate
2. Code

public static ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        }
        if (l2 == null) {
            return l1;
        }
        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }

4. Delete duplicate nodes from the ordered list

1. overview

2. way of thinking

1. direct method
   1. Since the input list has been sorted, we can determine whether it is a duplicate node by comparing the value of the node with the value of the node after it. If it is repeated, change the next pointer of the current node so that it jumps to the next node and points directly to the node after the next node
2. recursion
   1. Recursion, head.next = deleteDuplicates(head.next), the nodes will be pushed into the stack in turn, and finally taken out for comparison. If they are the same, the next node will be returned, otherwise the current node will be returned

3. code

public static ListNode deleteDuplicates(ListNode head){
        if (head==null||head.next==null){
            return head;
        }
        head.next = deleteDuplicates(head.next);
        return head.val == head.next.val?head.next:head;
    }

    public static ListNode deleteDuplicates2(ListNode head){
        ListNode current = head;
        while (current!=null||current.next!=null){
            if (current.val==current.next.val){
                current.next = current.next.next;
            }else {
                current = current.next;
            }
        }
        return head;
    }

5. Delete the nth last node of the linked list

1. overview

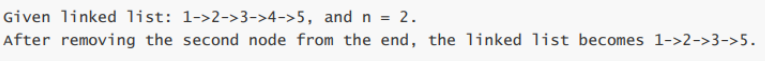
2. way of thinking

1. You can create two pointers: fast pointer and slow pointer. The fast pointer will go n steps first, and then the fast pointer will go to the end of the list together. At this time, the position of slow pointer is the previous node to be deleted.

3. code

public static ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode fast = head;
        ListNode slow = head;

        while (n-- > 0) {
            fast = fast.next;
        }
        if (fast == null) {
            return head.next;
        }
        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }
        slow.next = slow.next.next;
        return head;
    }

6. Adjacent nodes in the exchange list

1. overview

2. way of thinking

1. iteration
   1. Create a node (to record the final result), next points to head, and create the variable pre=node (pre is used to move the subscript of the linked list)
   2. When pre.next! = null & & pre.next.next! = null, create l1 as the pre.next node, l2 as the pre next.next node, and record node next=l2.next. And then start switching
   3. l1.next points to next, l2.next points to l1, and pre.next points to L2. Complete the exchange, move the pre position to l1
   4. return to node.next
2. recursion
   1. Start recursion from the head node of the linked list
   2. Each recursion is responsible for exchanging a pair of nodes. Two nodes to be exchanged are represented by firstNode and secondNode
   3. The next recursion is to pass the next pair of nodes to be exchanged. If there are nodes in the list, continue recursion
   4. After two nodes are exchanged, the second node is returned, because it is the new header after exchange
   5. After all nodes are exchanged, we return to the exchanged header, which is actually the second node of the original linked list

3. code

public static ListNode swapPairs(ListNode head) {
        ListNode node = new ListNode(-1);
        node.next = head;
        ListNode pre = node;
        while (pre.next != null && pre.next.next != null) {
            ListNode l1 = pre.next;
            ListNode l2 = pre.next.next;
            ListNode next = l2.next;

            l1.next = next;
            l2.next = l1;
            pre.next = l2;

            pre = l1;
        }
        return node.next;
    }

    public static ListNode swapPairs2(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode first = head;
        ListNode second = head.next;
        first.next = swapPairs2(second.next);
        second.next = first;

        return second;
    }

7. Sum of chain list

1. overview

2. way of thinking

1. Create two stacks to store the values of the two linked lists, create the head node to fix the head node of the linked list to be created later, and record the number of carry required for carry traversal
2. When l1Stack or l2Stack is not null, or carry!=0 (indicates carry is required), a while loop is performed
3. When L1 stack is not null, the top element of the stack is taken out. Otherwise, it is 0 and set to traverse X. When L1 stack is not null, the top element of the stack is taken out. Otherwise, it is 0 and set to traverse y. sum is x+y+carry.
4. After the calculation results are obtained, a new node is created with the node value of sum%10, and then connected with the head node. node.next=head.next，head.next=node
5. Finally, carry=sum/10 is required to record carry
6. Return to head.next

3. code

public static ListNode addTwoNumers(ListNode l1, ListNode l2) {
        Stack<Integer> l1Stack = bulidStack(l1);
        Stack<Integer> l2Stack = bulidStack(l2);
        ListNode head = new ListNode(-1);
        int carry = 0;
        while (!l1Stack.isEmpty() || !l2Stack.isEmpty() || carry != 0) {
            int x = l1Stack.isEmpty() ? 0 : l1Stack.pop();
            int y = l2Stack.isEmpty() ? 0 : l2Stack.pop();
            int sum = x + y + carry;
            ListNode node = new ListNode(sum % 10);
            node.next = head.next;
            head.next = node;
            carry = sum / 10;
        }
        return head.next;
    }

    private static Stack<Integer> bulidStack(ListNode l) {
        Stack<Integer> stack = new Stack<>();
        while (l != null) {
            stack.push(l.val);
            l = l.next;
        }
        return stack;
    }

8. Palindrome list

1. overview

LeetCode234

2. way of thinking

Method 1: copy the value into the array and use the double finger method

1. Copy linked list value to array list
2. To judge whether it is palindrome by double finger needling

Method 2: fast and slow pointer method (O(n) time complexity and O(1) space complexity)

1. Create slow pointer slow=head, fast pointer fast=head.next. When fast is not null or fast.next is not null, slow pointer takes one step and fast pointer takes two steps
2. If fast!=null, even nodes, let slow execute the next node
3. Then the segmentation is performed. When head.next=slow, exit the while loop, otherwise head=head.next. Disconnect the first half of the list, head.next=null
4. Reverse the second half of the list and compare the values

3. code

public static boolean isPalindrome(ListNode head) {
        if (head == null || head.next == null) {
            return true;
        }
        ListNode slow = head, fast = head.next;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        if (fast != null) {
            slow = slow.next; // Even node, let slow point to the next node
        }
        cut(head, slow); //Cut into two lists
        return isEqual(head, reverse(slow));
    }

    private static boolean isEqual(ListNode l1, ListNode l2) {
        while (l1 != null && l2 != null) {
            if (l1.val != l2.val)
                return false;
            l1 = l1.next;
            l2 = l2.next;
        }
        return true;
    }

    private static ListNode reverse(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode next = head.next;
        ListNode newHead = reverse(next);
        next.next = head;
        head.next = null;
        return newHead;
    }

    private static void cut(ListNode head, ListNode cutNode) {
        while (head.next != cutNode) {
            head = head.next;
        }
        head.next = null;
    }


    public static boolean isPalindrome2(ListNode head) {
        List<Integer> list = new ArrayList<>();
        while (head != null) {
            list.add(head.val);
            head = head.next;
        }

        int l = 0;
        int r = list.size() - 1;
        while (l < r) {
            if (list.get(l) != (list.get(r))) {
                return false;
            }
            l++;
            r--;
        }
        return true;
    }

9. Separated list

1. overview

1. Given a link list whose node is root, a function is written to divide the link list into k consecutive parts. The length of each part should be as equal as possible: the length difference between any two parts should not exceed 1, that is to say, some parts may be null, K parts should be output in the order of appearing in the list, and the length of the part in front should be greater than or equal to the length of the later part

2. way of thinking

1. Create traversal N to record the length of the original linked list, which is used to calculate the length of each partition. size=N/k (the minimum length of each partition), mod=N%k (more partitions are needed at the beginning). For example, the linked list with length of 10 is divided into three partitions, and the first partition has one more element
2. Create a linked list array with a capacity of k. when the cur node is not null, the for loop traverses the partition
   1. Calculate the length of each partition's linked list cursize = size + (MOD -- > 0? 1:0)
   2. After calculating the partition length, move the cur node backward
3. Link list
   1. Record that the next node of cur is next
   2. Set cur.next = null
   3. cur = next

3. code

public static ListNode[] splitListToParts(ListNode root, int k) {
        int N = 0;
        ListNode cur = root;
        while (cur!=null){
            N++;
            cur = cur.next;
        }
        int mod = N%k;
        int n = N/k;
        ListNode[] ret = new ListNode[k];
        cur = root;
        for (int i = 0;cur!=null&& i < k; i++) {
            ret[i] = cur;
            int curSize = n+(mod-->0?1:0);
            for (int j = 0; j < curSize - 1; j++) {
                cur = cur.next;
            }
            ListNode next = cur.next;
            cur.next = null;
            cur = next;
        }
        return ret;
    }

10. Link list elements gather by parity

1. overview

1. Given a linked list, all odd and even nodes are arranged together. The odd and even nodes here refer to the parity of node numbers, not the parity of node values (LeetCode328)

2. way of thinking

1. A LinkedList needs a head pointer and a tail pointer to support two terminal operations
2. Use the variables head and odd to save the head and tail pointers of the odd list. evenHead and even hold the head and tail pointers of the even list. The algorithm will traverse the original list once and put odd nodes in odd list and even nodes in even list.
3. Traversing the entire list also requires a pointer as an iterator. Here, the odd and even t pointers are not only tail pointers, but also iterators of the original linked list

3. code

public static ListNode oddEvenList(ListNode head) {
        if (head == null) {
            return head;
        }
        ListNode odd = head, even = head.next, evenHead = even;
        while (even != null && even.next != null) {
            odd.next = odd.next.next;
            odd = odd.next;
            even.next = even.next.next;
            even = even.next;
        }
        odd.next = evenHead;
        return head;
    }