leetcode lecture on algorithm interview in Dachang 12. Heap
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
Extension:
Full binary tree: all nodes except leaf nodes have two child nodes. This kind of binary tree is called full binary tree, as shown in the following figure:
Complete binary tree: if the height of the binary tree is h, the number of nodes in other layers (1 ~ h-1) reaches the maximum except layer h, and layer h lacks several nodes continuously from right to left, which is a complete binary tree.
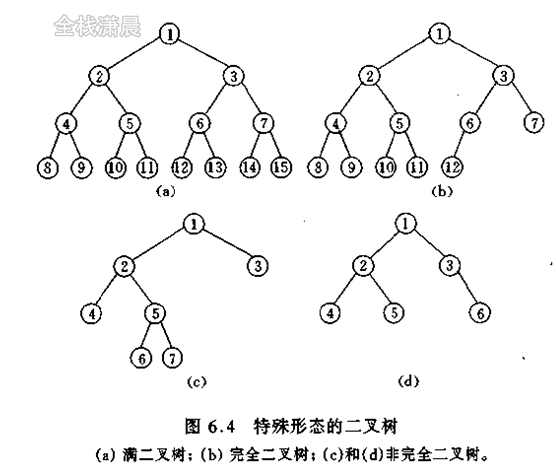
The heap is a complete binary tree, so we can implement it by array without wasting too much space. The value of each node in the heap is always not greater than or less than the value of its parent node. The heap is divided into large top heap and small top heap. The top of large top heap is the largest of the elements, and the top of small top heap is the smallest. When adding elements to the heap, we can dynamically adjust the order of elements in the heap The nature of the heap is always maintained.
Characteristics of reactor:
- The internal data is orderly
- Elements at the top of the heap can be ejected. The large top heap is the maximum value and the small top heap is the minimum value
- After each new element is added or the top element is popped up, the heap is reorganized to require O(logn) time.
Implementation of heap
- Implemented with an array, the heap corresponds to the elements in the array one by one from top to bottom and from left to right
- Node parent node index parentIndex = [(index - 1) / 2], left node index leftIndex = index * 2 + 1, right node index rightIndex = index * 2 + 2
- The first non leaf node is [size / 2]
Add elements to the heap
- Add the new data to the last element of the tree, that is, the end of the array
- Adjust the end node upward, that is, bubbleUp
- Time complexity O(logn)
The animation is too large. Click to view it
Pop up elements in the heap
- Exchange the values of the root node and the last node
- Delete last node
- Adjust the root node down
- Time complexity O(logn)
The animation is too large. Click to view it
Complexity of getting the minimum value from an array:
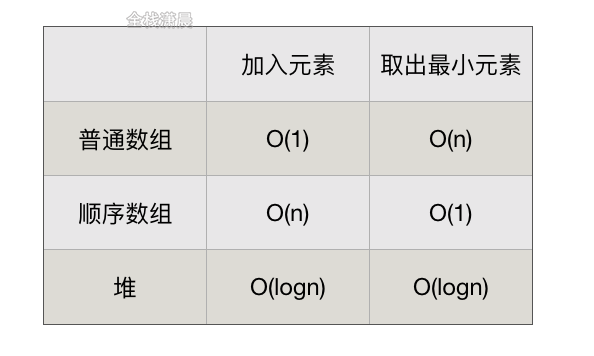
Complete code
class Heap {
constructor(comparator = (a, b) => a - b, data = []) {
this.data = data;
this.comparator = comparator;//comparator
this.heapify();//Heap
}
heapify() {
if (this.size() < 2) return;
for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
this.bubbleDown(i);//bubbleDown operation
}
}
peek() {
if (this.size() === 0) return null;
return this.data[0];//View the top of the heap
}
offer(value) {
this.data.push(value);//Add array
this.bubbleUp(this.size() - 1);//Adjust the position of the added elements in the small top heap
}
poll() {
if (this.size() === 0) {
return null;
}
const result = this.data[0];
const last = this.data.pop();
if (this.size() !== 0) {
this.data[0] = last;//Swap the first and last elements
this.bubbleDown(0);//bubbleDown operation
}
return result;
}
bubbleUp(index) {
while (index > 0) {
const parentIndex = (index - 1) >> 1;//Location of parent node
//If the current element is smaller than the element of the parent node, the positions of the current node and the parent node are exchanged
if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
this.swap(index, parentIndex);//Swap the location of yourself and the parent node
index = parentIndex;//Continuously take up the parent node for comparison
} else {
break;//If the current element is larger than the element of the parent node, it does not need to be processed
}
}
}
bubbleDown(index) {
const lastIndex = this.size() - 1;//Location of the last node
while (true) {
const leftIndex = index * 2 + 1;//Location of left node
const rightIndex = index * 2 + 2;//Location of the right node
let findIndex = index;//Location of the bubbleDown node
//Find the node with small value in the left and right nodes
if (
leftIndex <= lastIndex &&
this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
) {
findIndex = leftIndex;
}
if (
rightIndex <= lastIndex &&
this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
) {
findIndex = rightIndex;
}
if (index !== findIndex) {
this.swap(index, findIndex);//Swap the current element and the small value in the left and right nodes
index = findIndex;
} else {
break;
}
}
}
swap(index1, index2) {//Swap the positions of the two elements in the heap
[this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
}
size() {
return this.data.length;
}
}