leetcode essence of Dachang algorithm interview 20. String
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
5. Longest palindrome substring (medium)
Method 1. Dynamic programming
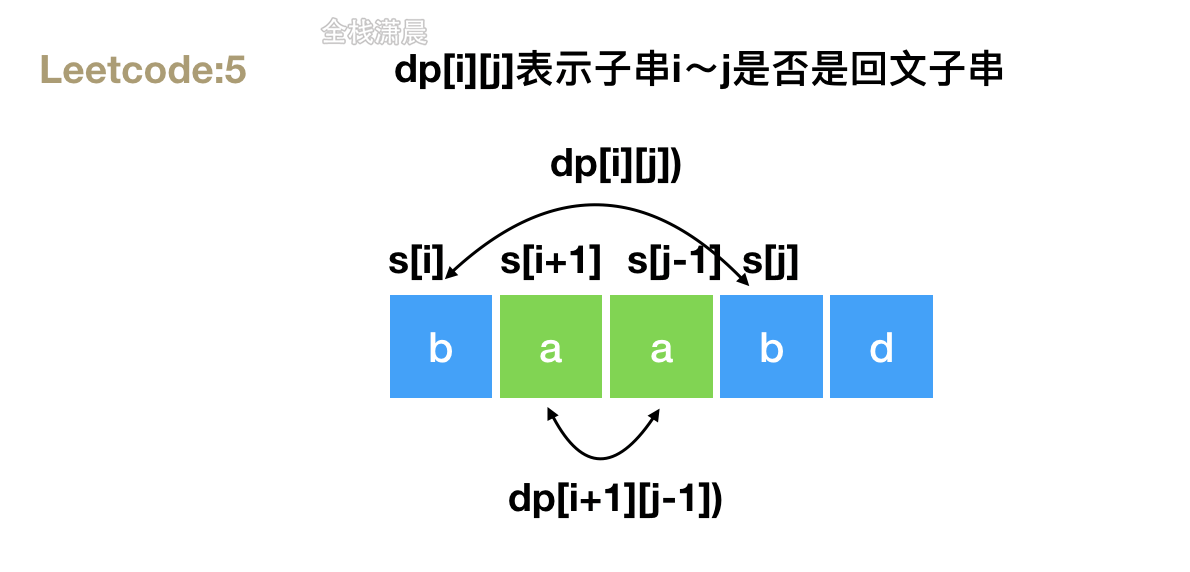
- Idea: define dp[i][j] to indicate whether the substrings I ~ j are palindrome substrings. Cycle the substrings of s to see whether s[i] and s[j] are equal. If they are equal, whether dp[i][j] is palindrome substring depends on whether dp[i+1][j-1] is also palindrome substring. Constantly update the length of the maximum palindrome substring during the cycle. Note that the length of the substring is 0 or 1
- Complexity: time complexity O(n^2), two-level cycle. Space complexity O(n^2), that is, the space of dynamic programming dp array.
Js:
var longestPalindrome = function(s) {
let n = s.length;
let res = '';
let dp = Array.from(new Array(n),() => new Array(n).fill(false));//Initialize array
for(let i = n-1;i >= 0;i--){//Circular string
for(let j = i;j < n;j++){
//dp[i][j] indicates whether the substrings I ~ j are palindrome substrings
//Palindrome substring must satisfy s[i], s[j] equality. And the outward extension of one character is also equal, that is, dp[i+1][j-1] is also a palindrome substring
//J - I < 2 indicates that the substring less than or equal to 1 is also a palindrome string
dp[i][j] = s[i] == s[j] && (j - i < 2 || dp[i+1][j-1]);
if(dp[i][j] && j - i +1 > res.length){//The current palindrome substring is larger than the previous one, and the maximum length is updated
res = s.substring(i,j+1);
}
}
}
return res;
};
Java:
public String longestPalindrome(String s) {
int N = s.length();
boolean[][] dp = new boolean[N][N];
String res = "";
for (int i = N - 1; i >= 0; i--) {
for (int j = i; j < N; j++) {
if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
dp[i][j] = true;
}
if (dp[i][j] && (j - i + 1) > res.length()) {
res = s.substring(i, j + 1);
}
}
}
return res;
}
Method 2. Central diffusion method
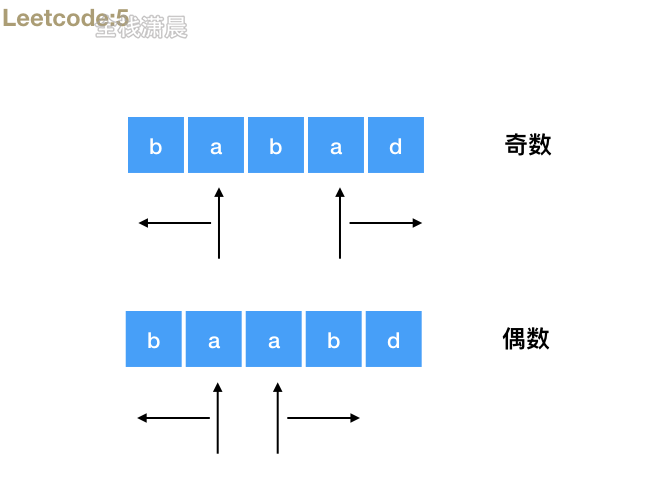
- Idea: when the longest palindrome substring is odd or even, define start as the index at the beginning of the longest palindrome substring, then cycle the string, continuously expand the length of the palindrome string, update the length of the largest palindrome substring and the position of start during the cycle, and finally return the substring from start to start+ maxLength
- Complexity: time complexity O(n^2). The string is cycled once, and the interior of each cycle expands outward. Space complexity O(1)
Js:
var longestPalindrome = function (s) {
if (s.length <= 0) {//boundary condition
return s;
}
let start = 0;//Index at the beginning of the longest palindrome substring
let maxLength = 1;//Initialize maximum palindrome substring length
function h(left, right) {
//When s[left], and s[right] want to wait, continue to expand the length of the palindrome string
while (left >= 0 && right < s.length && s[left] === s[right]) {
if (right - left + 1 > maxLength) {
maxLength = right - left + 1;//Update the length of the maximum palindrome substring
start = left;//Update the location of start
}
left--;
right++;
}
}
for (let i = 0; i < s.length; i++) {
h(i - 1, i + 1);//Palindrome substrings are odd
h(i, i + 1);//Palindrome substrings are even
}
return s.substring(start, start + maxLength);
};
Java:
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) {
return "";
}
//Defines the length of the longest palindrome substring
int maxLength = 1;
//Defines the starting position of the longest palindrome substring
int start = 0;
//Traverses the center of a possible palindrome substring
for (int i = 0; i < s.length() - 1; i++) {
//When the length of the longest palindrome substring is odd, the center position is one character
int oddLength = expandAroundCenter(s, i, i);
//When the length of the longest palindrome substring is even, the center position is two characters
int evenLength = expandAroundCenter(s, i, i + 1);
int length = Math.max(oddLength, evenLength);
//Find the maximum length
if (maxLength < length) {
maxLength = length;
//Calculate start position
start = i - (maxLength - 1) / 2;
}
}
//Intercept string
return s.substring(start, start + maxLength);
}
//Returns the length of the longest palindrome substring
public int expandAroundCenter(String s, int left, int right) {
while (left >= 0 && right < s.length()) {
if (s.charAt(left) == s.charAt(right)) {
//The boundary extends outward
left--;
right++;
} else {
break;
}
}
//If the last outward expansion does not meet the conditions, restore the expansion
left++;
right--;
return right - left + 1;
}
}
680. Validate palindrome string II (easy)
- Idea: the collision pointer constantly judges whether the numbers on the left and right sides are equal. If they are not equal, there is another chance. The left pointer moves forward or the right pointer moves backward to continue verification
- Complexity: time complexity O(n), space complexity O(1).
example:
input: s = "aba" output: true input: s = "abca" output: true explain: You can delete c Character.
js:
function isPalindrome(str, l, r) {
while (l < r) { //The collision pointer constantly judges whether the numbers on both sides are equal
if (str[l] != str[r]) {
return false;
}
l++;
r--;
}
return true;
}
var validPalindrome = function (str) {
let l = 0, r = str.length - 1; //Head and tail pointer
while (l < r) {
if (str[l] != str[r]) {//If the left and right pointers are different, there is another chance. The left pointer moves forward or the right pointer moves backward to continue verification
return isPalindrome(str, l + 1, r) || isPalindrome(str, l, r - 1);
}
l++;
r--;
}
return true;
};
java:
class Solution {
public boolean validPalindrome(String s) {
int l = 0, r = s.length() - 1;
while (l < r) {
char c1 = s.charAt(l), c2 = s.charAt(r);
if (c1 == c2) {
++l;
--r;
} else {
return validPalindrome(s, l, r - 1) || validPalindrome(s, l + 1, r);
}
}
return true;
}
public boolean validPalindrome(String s, int l, int r) {
for (int i = l, j = r; i < j; ++i, --j) {
char c1 = s.charAt(i), c2 = s.charAt(j);
if (c1 != c2) {
return false;
}
}
return true;
}
}
32. Longest valid bracket (hard)
Method 1. Dynamic programming
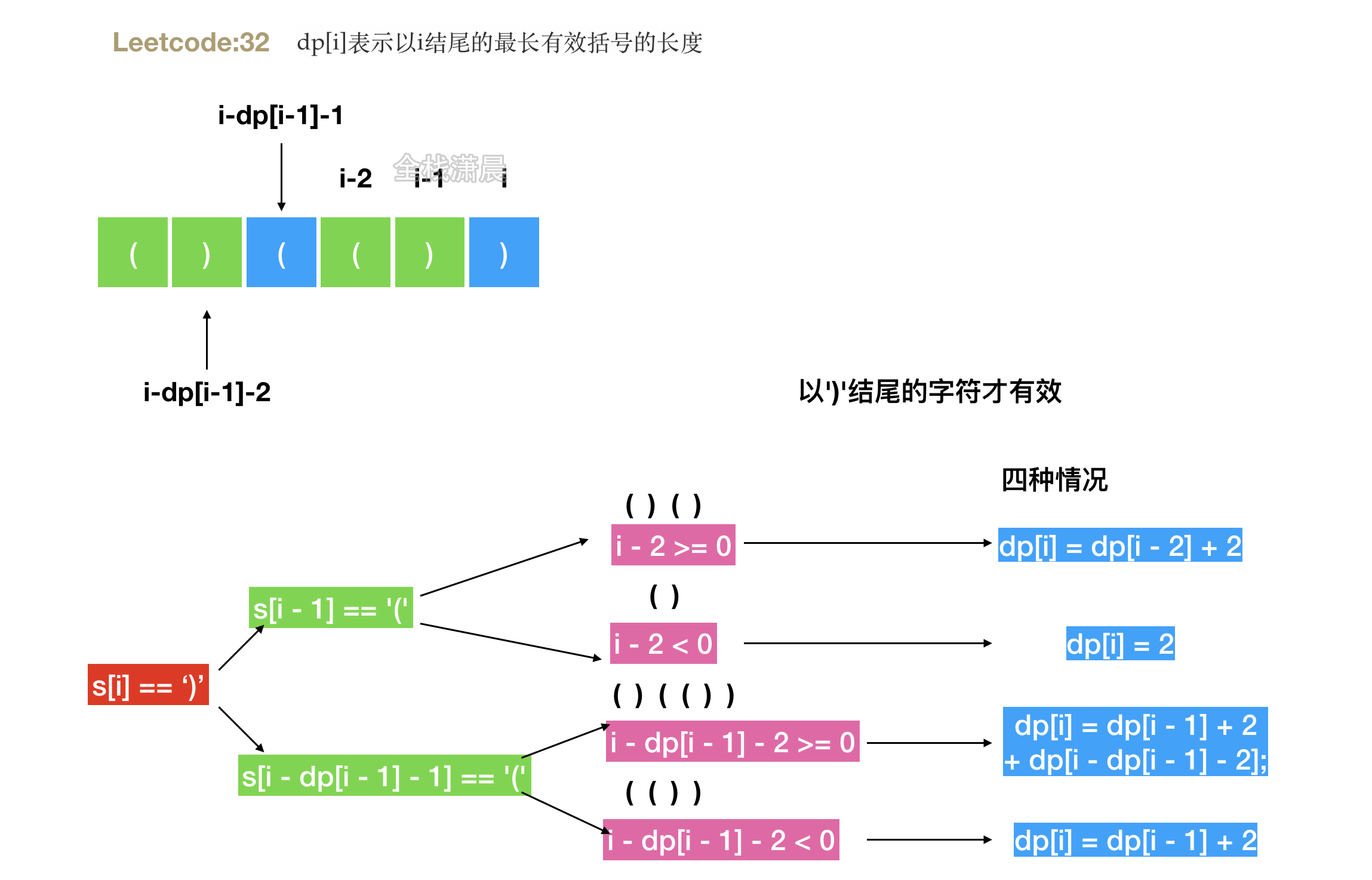
- Idea: dp[i] indicates the length of the longest valid bracket ending with I. there are four cases. See the figure
- Complexity: time complexity O(n), n is the length of the string, traversing once in total. Space complexity O(n), that is, the space of dp array
js:
const longestValidParentheses = (s) => {
let maxLen = 0;
const len = s.length;
const dp = new Array(len).fill(0);
for (let i = 1; i < len; i++) {
if (s[i] == ')') {//Only characters ending with ')' are valid
if (s[i - 1] == '(') {//If the previous position is' (', it can form valid parentheses with the current character
if (i - 2 >= 0) {//If there is a string in the first two positions
dp[i] = dp[i - 2] + 2;//The current status is equal to the 2 characters currently matched plus the longest character length matched in the first two positions
} else {//If there is no string in the first 2 positions
dp[i] = 2;//The current status is equal to the current matching 2 characters
}
//A valid character ending in i-1 can form valid parentheses with the current character if it is' ('in a forward position
} else if (s[i - dp[i - 1] - 1] == '(') {
if (i - dp[i - 1] - 2 >= 0) {//Valid characters ending with i-1 are 2 positions forward if > = 0
//Current status = valid character length ending with i-1 + 2 valid parentheses currently matched + valid character length ending with i - dp[i - 1] - 2
dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] - 2];
} else {
//Valid characters ending in i-1 are 2 positions forward if < 0
//Current status = valid character length ending with i-1 + 2 valid parentheses currently matched
dp[i] = dp[i - 1] + 2;
}
}
}
maxLen = Math.max(maxLen, dp[i]);
}
return maxLen;
};
Java:
class Solution {
public int longestValidParentheses(String s) {
int maxLen = 0;
int[] dp = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxLen = Math.max(maxLen, dp[i]);
}
}
return maxLen;
}
}
Method 2. Stack
- Idea: traverse the string, prepare a stack, store the string subscript, first put the initial reference - 1, encounter '(' in the stack, encounter ')' out of the stack, and judge the stack length. If it is not empty, update the maximum legal string length, otherwise put the current subscript into the stack
- Complexity: time complexity O(n), n is the length of the string, traversing once in total. Space complexity O(n), that is, the space of the stack
The animation is too large. Click to view it
js:
var longestValidParentheses = function (s) {
let maxLen = 0
let stack = []
stack.push(-1) // Initialize a reference
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
// (in stack) out stack
stack.push(i)
} else {
// )Out of the stack
stack.pop()
if (stack.length) {
// Calculate the current effective continuous length for each stack
// How to calculate the current position of continuous length - stack top subscript
maxLen = Math.maxLen(maxLen, i - stack[stack.length - 1])
} else {
stack.push(i) //When the stack is empty, the reference in the right bracket indicates that the length needs to be recalculated from this subscript
}
}
}
return maxLen
};
java:
class Solution {
public int longestValidParentheses(String s) {
int maxLen = 0;
Deque<Integer> stack = new LinkedList<Integer>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.isEmpty()) {
stack.push(i);
} else {
maxLen = Math.max(maxLen, i - stack.peek());
}
}
}
return maxLen;
}
}
Method 3. Double traversal
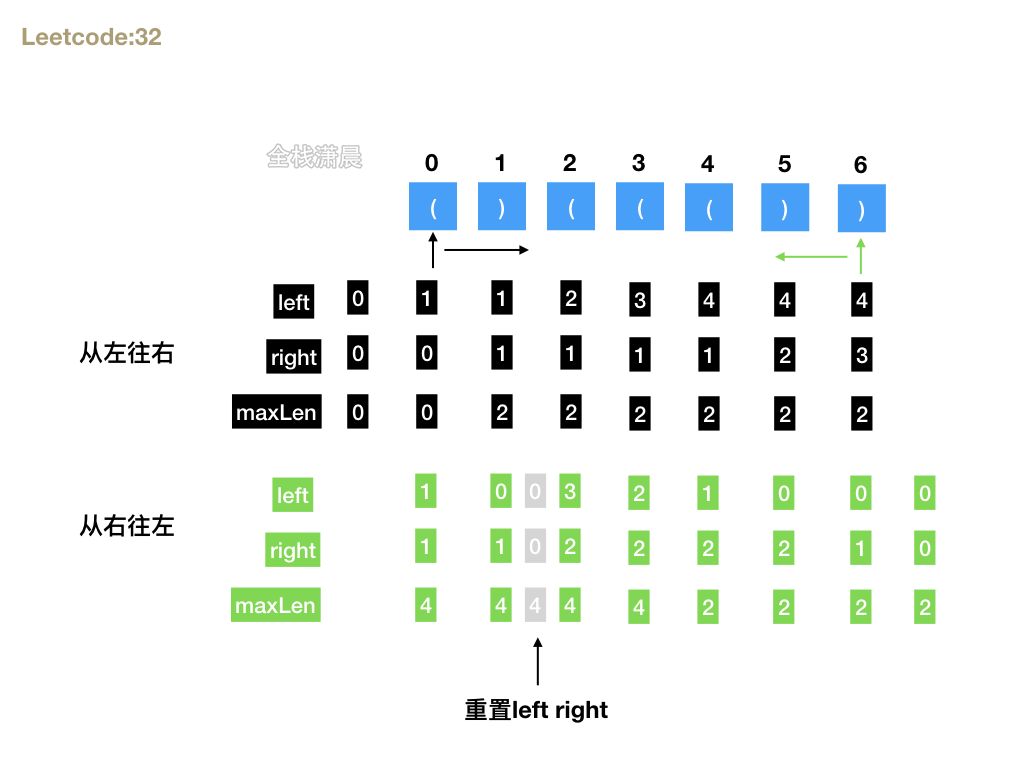
- Idea: traverse the string from left to right, from right to left, and encounter '(', left + +, encounter ')', right + +. When the number of left and right parentheses is the same, update the maximum length. If right is greater than left, reset left and right and count again
- Complexity: time complexity O(n), n is the length of the string, traversing 2 times in total. Space complexity O(1)
Js:
var longestValidParentheses = function (s) {
let maxLen = 0;
let left = 0;
let right = 0;
for (let i = 0; i < s.length; i++) {//From left to right
if (s[i] == "(") { //Meet '(' left++
left++;
} else {
right++; //Meet ')' right++
}
if (left == right) { //Same quantity on the left and right
maxLen = Math.max(maxLen, 2 * left); //Update maximum length
} else if (right > left) { //Right is greater than left reset left right re count
left = right = 0;
}
}
left = right = 0;
for (let i = s.length - 1; i >= 0; i--) { //From right to left
if (s[i] == "(") {
left++;
} else {
right++;
}
if (left == right) {
maxLen = Math.max(maxLen, right * 2);
} else if (left > right) {
left = right = 0;
}
}
return maxLen;
};
Java:
class Solution {
public int longestValidParentheses(String s) {
int left = 0, right = 0, maxLen = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxLen = Math.max(maxLen, 2 * right);
} else if (right > left) {
left = right = 0;
}
}
left = right = 0;
for (int i = s.length() - 1; i >= 0; i--) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxLen = Math.max(maxLen, 2 * left);
} else if (left > right) {
left = right = 0;
}
}
return maxLen;
}
}
301. Delete invalid parentheses (hard)
Method 1:bfs
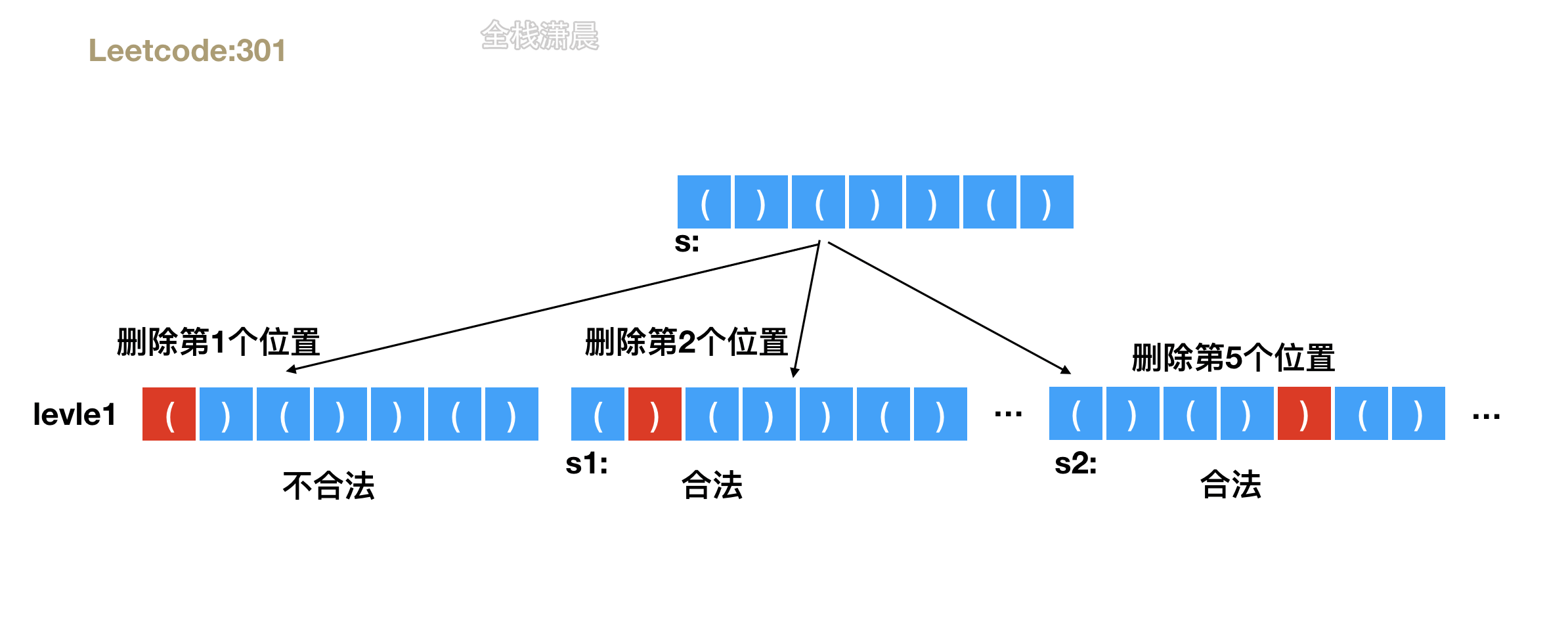
- Idea: the minimum number of deleted parentheses. This problem of seeking the shortest or the least number is associated with bfs. The first layer of bfs where the solution appears is the legal string formed by the shortest deleted parentheses. Prepare the queue to bfs search the string, and the legal string appears in the queue. Otherwise, try to delete a character and enter the next layer for judgment. Note that the legal characters may be repeated and need to be deleted Heavy.
js:
var removeInvalidParentheses = function (s) {
let res = [];
let queue = [];
let visited = new Set();//duplicate removal
queue.push(s);
while (true) {
let size = queue.length;//[s]
for (let i = 0; i < size; i++) {
s = queue.shift();//Out of the team
if (isVaild(s)) {//If it is a legal string
res.push(s);//Add result array
} else if (res.length == 0) {//Illegal and res.length == 0, enter the next layer of bfs and try to delete characters
for (let i = 0; i < s.length; i++) {
if (s[i] == '(' || s[i] === ')') {//Is the left and right parentheses. Try to delete the characters, otherwise skip
let nexts = s.substring(0, i) + s.substring(i + 1);
if (!visited.has(nexts)) {//Judge whether the newly generated string is repeated
queue.push(nexts);//Join the queue and enter the next layer [s1,s2...]
visited.add(nexts);//Add de duplication array
}
}
}
}
}
if (res.length > 0) {//The layer where the legal string appears, terminate the loop
break;
}
}
return res;
};
function isVaild(s) {
let count = 0;
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {//Left parenthesis count+1
count++;
} else if (s[i] === ')') {//Right parenthesis count-1
count--;
}
if (count < 0) {//Less than 0 means there are many right parentheses
return false;
}
}
return count === 0;
}
java:
public class Solution {
public List<String> removeInvalidParentheses(String s) {
List<String> res = new ArrayList<>();
if (s == null) {
return res;
}
Set<String> visited = new HashSet<>();
visited.add(s);
Queue<String> queue = new LinkedList<>();
queue.add(s);
boolean found = false;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
String front = queue.poll();
if (isValid(front)) {
res.add(front);
found = true;
}
int currentWordLen = front.length();
char[] charArray = front.toCharArray();
for (int j = 0; j < currentWordLen; j++) {
if (front.charAt(j) != '(' && front.charAt(j) != ')') {
continue;
}
String next = new String(charArray, 0, j) + new String(charArray, j + 1, currentWordLen - j - 1);
if (!visited.contains(next)) {
queue.offer(next);
visited.add(next);
}
}
}
if (found) {
break;
}
}
return res;
}
public boolean isValid(String s) {
char[] charArray = s.toCharArray();
int count = 0;
for (char c : charArray) {
if (c == '(') {
count++;
} else if (c == ')') {
count--;
}
if (count < 0) {
return false;
}
}
return count == 0;
}
}
387. First unique character in a string (easy)
Method 1: hash table
- Idea: count the frequency of characters and find the index of the first character with frequency 1
- Complexity: time complexity O(n), space complexity O(k), and K is the size of the character set
js:
var firstUniqChar = function (s) {
const counts = new Array(26).fill(0); //An array with a length of 26 stores the number of occurrences of characters
for (const c of s) { //Traverse s and count the number of occurrences of each character
counts[c.charCodeAt(0) - 97]++; //97 is the Unicode value of a
}
for (let i = 0; i < s.length; i++) { //Traverse s again
if (counts[s[i].charCodeAt(0) - 97] == 1) {//Find the index of the first character with frequency 1
return i;
}
}
return -1;
};
java:
class Solution {
public int firstUniqChar(String s) {
Map<Character, Integer> frequency = new HashMap<Character, Integer>();
for (int i = 0; i < s.length(); ++i) {
char ch = s.charAt(i);
frequency.put(ch, frequency.getOrDefault(ch, 0) + 1);
}
for (int i = 0; i < s.length(); ++i) {
if (frequency.get(s.charAt(i)) == 1) {
return i;
}
}
return -1;
}
}
Method 2: queue
- Idea: loop the string s. if the current character does not appear in the map, add the string and location index to the map and queue. When a duplicate character appears, the value corresponding to the character in the map is set to - 1. If the value corresponding to the queue head element in the map is - 1, it indicates that it is a duplicate element. Keep going out of the queue until the queue head is a non duplicate element. After the loop ends, if there are elements in the queue, the queue header is the first non repeating character
- Complexity: time complexity O(n), space complexity O(k), and K is the size of the character set
js:
var firstUniqChar = function(s) {
const position = new Map();
const q = [];
for (let [i, ch] of Array.from(s).entries()) {
//Loop the string s. if the current character does not appear in the map, the string and location index are added to the map and queue
if (!position.has(ch)) {
position.set(ch, i);
q.push([ch, i]);
} else {
position.set(ch, -1);//When duplicate characters appear, the value corresponding to the characters in the map is set to - 1
//If the value of the queue head element in the map is - 1, it indicates that it is a repeating element. Keep going out of the queue until the queue head is a non repeating element
while (q.length && position.get(q[0][0]) === -1) {
q.shift();
}
}
}
return q.length ? q[0][1] : -1;//If there are elements in the queue, the queue header is the first non repeating character
};
java:
class Solution {
public int firstUniqChar(String s) {
Map<Character, Integer> position = new HashMap<Character, Integer>();
Queue<Pair> queue = new LinkedList<Pair>();
int n = s.length();
for (int i = 0; i < n; ++i) {
char ch = s.charAt(i);
if (!position.containsKey(ch)) {
position.put(ch, i);
queue.offer(new Pair(ch, i));
} else {
position.put(ch, -1);
while (!queue.isEmpty() && position.get(queue.peek().ch) == -1) {
queue.poll();
}
}
}
return queue.isEmpty() ? -1 : queue.poll().pos;
}
class Pair {
char ch;
int pos;
Pair(char ch, int pos) {
this.ch = ch;
this.pos = pos;
}
}
}
14. Longest common prefix (easy)
- Idea: scan the string vertically to find the first different position
- Complexity: time complexity O(mn), m is the longest length of string, and n is the length of character array
f l o w e r f l o w f l i g h t
js:
var longestCommonPrefix = function(strs) {
if(strs.length == 0)
return "";
let ans = strs[0];//The initial value of ans is the first of the string array
for(let i =1;i<strs.length;i++) {//Circular string array
let j=0;
for(;j<ans.length && j < strs[i].length;j++) {//Loop the character to find the first different position
if(ans[j] != strs[i][j])
break;
}
ans = ans.substr(0, j);//Intercept the string from position 0 to the first different position
if(ans === "")
return ans;
}
return ans;
};
java:
class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs.length == 0)
return "";
String ans = strs[0];
for(int i =1;i<strs.length;i++) {
int j=0;
for(;j<ans.length() && j < strs[i].length();j++) {
if(ans.charAt(j) != strs[i].charAt(j))
break;
}
ans = ans.substring(0, j);
if(ans.equals(""))
return ans;
}
return ans;
}
}
344. Reverse string (easy)
- Idea: the pointer left initially points to position 0 and right initially points to position n-1. Double pointers constantly swap elements at left and right positions
- Complexity: time complexity O(n). Space complexity O(1)
js:
var reverseString = function(s) {
const n = s.length;
//Double pointers constantly swap elements at left and right positions
for (let left = 0, right = n - 1; left < right; left++, right--) {
[s[left], s[right]] = [s[right], s[left]];
}
};
java:
class Solution {
public void reverseString(char[] s) {
int n = s.length;
for (int left = 0, right = n - 1; left < right; left++, right--) {
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
}
}
}
151. Flip the words in the string (medium)
Method 1: regular
- Idea: remove the spaces at the beginning and end of the string, then replace those spaces with a regular space, separate them into an array according to the spaces, and then flip back to the string
js:
var reverseWords = function(s) {
return s.trim().replace(/\s+/g, ' ').split(' ').reverse().join(' ')
};
java:
class Solution {
public String reverseWords(String s) {
s = s.trim();
List<String> wordList = Arrays.asList(s.split("\\s+"));
Collections.reverse(wordList);
return String.join(" ", wordList);
}
}
Method 2: double ended queue
- Idea: the left pointer is initially at position 0 and the right pointer is initially at position s.length - 1. Traverse the string, add each string separated by spaces to the queue, and finally turn back the string
- Complexity: time complexity O(n), space complexity O(n)
js:
//"the sky is blue"
var reverseWords = function(s) {
let left = 0
let right = s.length - 1
let queue = []
let word = ''
//Remove the left and right spaces
while (s.charAt(left) === ' ') left ++
while (s.charAt(right) === ' ') right --
while (left <= right) {
let char = s.charAt(left)
if (char === ' ' && word) {
queue.unshift(word)//Add string to queue
word = ''//Reset string
} else if (char !== ' '){//Splice a single string
word += char
}
left++
}
queue.unshift(word)//The last string is also added to the queue
return queue.join(' ')//Return string
};
java:
class Solution {
public String reverseWords(String s) {
int left = 0, right = s.length() - 1;
while (left <= right && s.charAt(left) == ' ') {
++left;
}
while (left <= right && s.charAt(right) == ' ') {
--right;
}
Deque<String> d = new ArrayDeque<String>();
StringBuilder word = new StringBuilder();
while (left <= right) {
char c = s.charAt(left);
if ((word.length() != 0) && (c == ' ')) {
d.offerFirst(word.toString());
word.setLength(0);
} else if (c != ' ') {
word.append(c);
}
++left;
}
d.offerFirst(word.toString());
return String.join(" ", d);
}
}
1143. Longest common subsequence (medium)
Method 1: dynamic programming

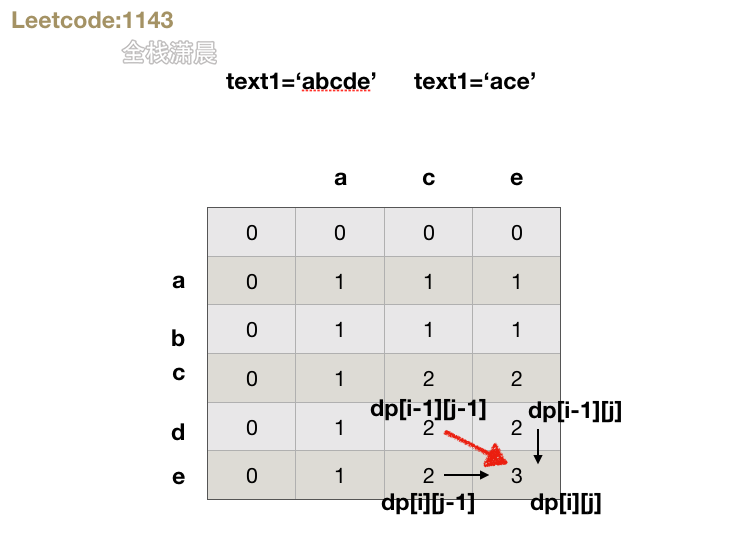
-
Idea: note that subsequences can be discontinuous
-
Status definition: dp[i][j] represents the longest common subsequence of text1[0:i-1] and text2[0:j-1]. Note that it is a closed interval. It is convenient to initialize the dp array because it reaches i-1 or j-1. When i=0 or j=0, it means that the null character matches another string. At this time, dp[i][j]=0
-
State transition equation: when text1[i - 1] == text2[j - 1]: dp[i][j] = dp[i - 1][j - 1] + 1
When text1 [I - 1]= Text2 [J - 1]: dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
-
Initialization of dp: when i = 0: dp[0][j]=0
When j = 0: dp[i][0]=0
-
Return result: dp[len(text1)][len(text2)]
-
-
Complexity: time complexity O(mn), space complexity O(mn)
js:
var longestCommonSubsequence = function(text1, text2) {
const m = text1.length, n = text2.length;
const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));//Initialize dp
for (let i = 1; i <= m; i++) {
const c1 = text1[i - 1];
for (let j = 1; j <= n; j++) {
const c2 = text2[j - 1];
if (c1 === c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;//When text1 and text2 characters are the same, the longest common subsequence length + 1
} else {
//When text1 and text2 characters are different, the longer of the longest common subsequence after text1 or text2 is reduced by one bit forward is returned
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
};
java:
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
if (c1 == c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
115. Different subsequences (hard)
Method 1. Dynamic programming
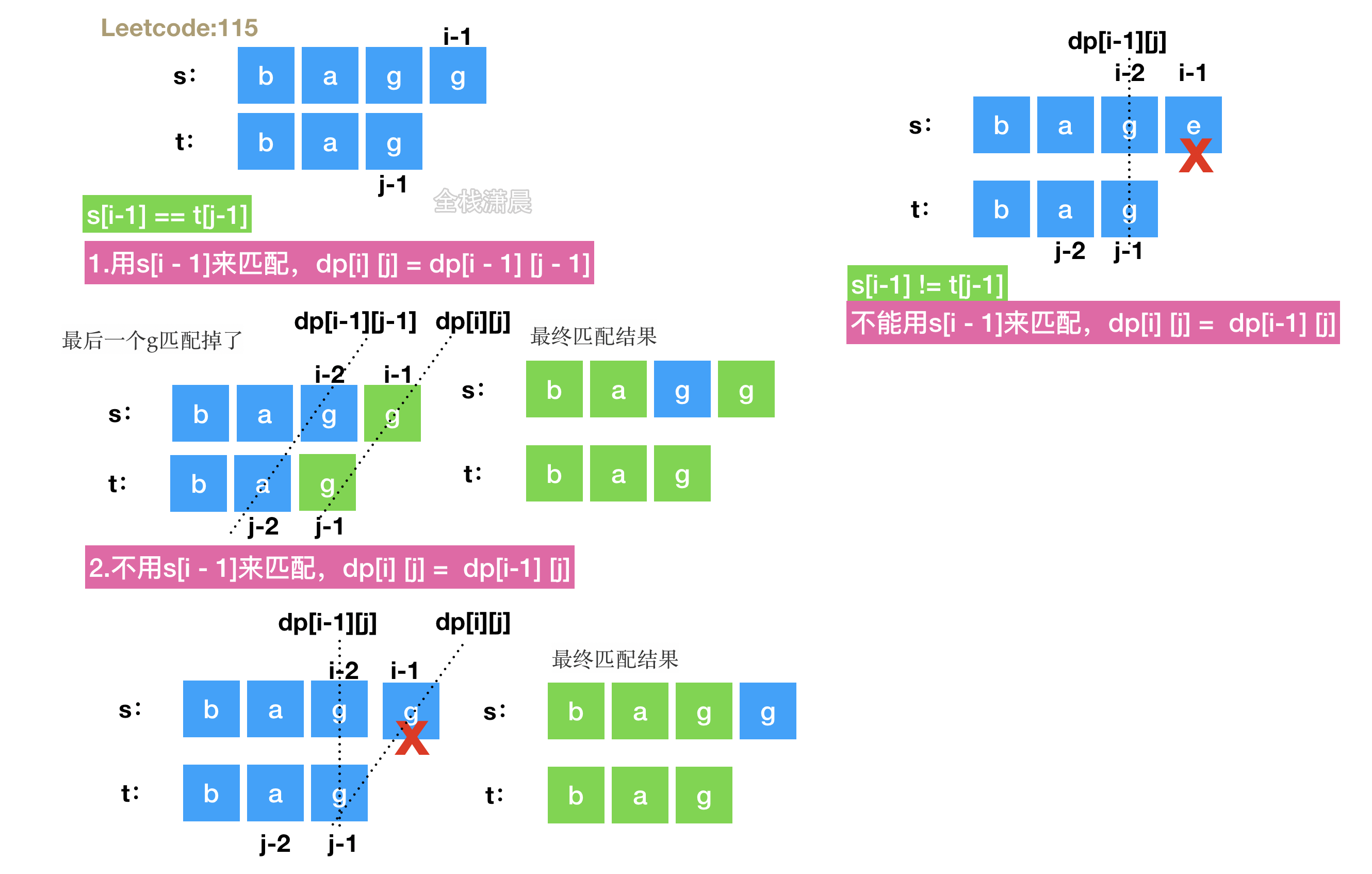
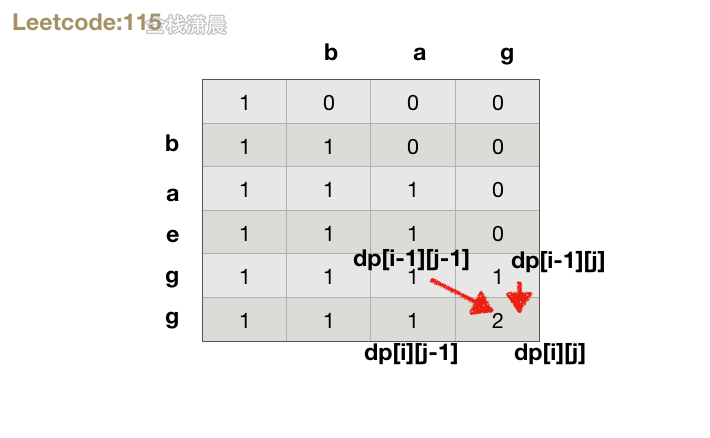
-
Idea: split the matching into different substrings. There are repeated substructures in these matching, which can be done by dynamic programming
-
State definition: dp[i][j] represents s ending with i-1, and the number of t ending with j-1 in its subsequence is dp[i][j]
-
State transition equation:
-
When s[i-1] == t[j-1]:
1. Match with s[i - 1], dp[i][j] = dp[i - 1][j - 1],
2. Do not use s[i - 1] to match, DP [i] [J] = DP [I-1] [J].
-
s[i-1] != When t [J-1]: s[i - 1] cannot be used for matching, dp[i][j] = dp[i-1][j]
-
-
Initial state:
- dp[i][0] =1: when j=0, it is equivalent to that t is an empty string. The empty character appears once in the substring of another string. At this time, the first column is initialized to 1.
- Other situations: dp[i][j] =0 during initialization
-
-
Complexity: time complexity O(mn), m and n are the lengths of s and t respectively. Space complexity O(mn), dp array space
js:
//dp[i][j] indicates that the number of t ending in j-1 in s subsequence ending in i-1 is dp[i][j]
const numDistinct = (s, t) => {
//Initialize dp array,
let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));
//When j=0, it is equivalent to that t is an empty string. The empty character appears once in the substring of another string. At this time, the first column is initialized to 1,
for(let i = 0; i <=s.length; i++) {
dp[i][0] = 1;
}
//When s[i-1] == t[j-1]:
//1. Match dp[i][j] = dp[i-1][j-1] with s[i - 1]
//2. Do not use s[i - 1] to match dp[i][j] = dp[i-1][j]
//When s[i-1]= t[j-1]: s[i-1] cannot be used to match, s[i-1] cannot match t[j-1], so dp[i][j] = dp[i-1][j]
for(let i = 1; i <= s.length; i++) {
for(let j = 1; j<= t.length; j++) {
if(s[i-1] === t[j-1]) {
dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
} else {
dp[i][j] = dp[i-1][j]
}
}
}
return dp[s.length][t.length];
};
java:
class Solution {
public int numDistinct(String s, String t) {
int[][] dp = new int[s.length() + 1][t.length() + 1];
for (int i = 0; i < s.length() + 1; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < s.length() + 1; i++) {
for (int j = 1; j < t.length() + 1; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}else{
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[s.length()][t.length()];
}
}
125. Validate palindrome string (easy)
Idea: use regular to remove irrelevant characters, and then collide with the pointer to judge whether the left and right sides are the same characters
Complexity: time complexity O(n), space complexity O(1)
js:
var isPalindrome = function (s) {
s = s.replace(/[\W|_]/g, "").toLowerCase();
if (s.length < 2) {
return true;
}
let left = 0;
let right = s.length - 1;
while (left < right) {
if (s[left] !== s[right]) {//The collision pointer determines whether the left and right sides are the same characters
return false;
}
left++;
right--;
}
return true;
};
java:
public boolean isPalindrome(String s) {
String lowerCase = s.toLowerCase();
int left = 0;
int right = lowerCase.length() - 1;
while (left < right) {
while (left < right && !Character.isLetterOrDigit(lowerCase.charAt(left))) {
left++;
}
while (left < right && !Character.isLetterOrDigit(lowerCase.charAt(right))) {
right--;
}
if (lowerCase.charAt(left) != lowerCase.charAt(right)) {
return false;
}
left++;
right--;
}
return true;
}
796. Rotate string (easy)
- Idea: repeat the string once to determine whether it contains another string
- Complexity: time complexity O(n^2). Compare whether one string contains the complexity O(n^2) of another string. Spatial complexity O(n)
js
var rotateString = function (A, B) {
return A.length <= B.length && (A + A).includes(B)
};
java:
class Solution {
public boolean rotateString(String A, String B) {
return A.length() == B.length() && (A + A).contains(B);
}
}
844. Compare strings with backspace (easy)

Method 1. Intercept the string, loop the string, and cut off the last character when # it is encountered. After the loop is completed, finally compare whether the two strings with # backspace removed are equal. The time complexity is O(m+n). m and N are the lengths of the two strings. Space complexity O(1)
Method 2. Double pointer
- Idea: the double pointer cycles from right to left. Each time, two characters are processed #, until the first character is the character after all the backspace on the right is processed, and then see whether the two characters are consistent
- Complexity: time complexity O(m+n). m and N are the lengths of two strings. Space complexity O(1)
js:
var backspaceCompare = function(S, T) {
let i = S.length - 1,
j = T.length - 1,
skipS = 0,
skipT = 0;
//Double pointer cycles from right to left
while(i >= 0 || j >= 0){
while(i >= 0){//Dispose # until the backspace on the right of the character pointed to by left is disposed of
if(S[i] === '#'){
skipS++;
i--;
}else if(skipS > 0){
skipS--;
i--;
}else break;
}
while(j >= 0){//Dispose # until the backspace to the right of the character pointed to by right is disposed of
if(T[j] === '#'){
skipT++;
j--;
}else if(skipT > 0){
skipT--;
j--;
}else break;
}
if(S[i] !== T[j]) return false;//If the strings after the backspace are not equal, false is returned
i--;//Continue the cycle
j--;
}
return true;//If false is not returned during the loop, true is returned at last
};
java:
class Solution {
public boolean backspaceCompare(String S, String T) {
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i >= 0 || j >= 0) {
while (i >= 0) {
if (S.charAt(i) == '#') {
skipS++;
i--;
} else if (skipS > 0) {
skipS--;
i--;
} else {
break;
}
}
while (j >= 0) {
if (T.charAt(j) == '#') {
skipT++;
j--;
} else if (skipT > 0) {
skipT--;
j--;
} else {
break;
}
}
if (i >= 0 && j >= 0) {
if (S.charAt(i) != T.charAt(j)) {
return false;
}
} else {
if (i >= 0 || j >= 0) {
return false;
}
}
i--;
j--;
}
return true;
}
}
557. Reverse word III in string (easy)
Method 1: with api
// "Let's take LeetCode contest"
const reverseWords = s => {
const arr = s.split(' ');
const res = [];
for (let i = 0; i < arr.length; i++) {
res.push(arr[i].split('').reverse().join(''));
}
return res.join(' ');
};
Method 2: double pointer
js:
// "Let's take LeetCode contest"
var reverseWords = function (s) {
let arr = s.split("");
let l = 0, r = l;
while (l < arr.length) {
//Find ending space
while (arr[r] && arr[r] !== " ") {
r++;
}
//Reverse word
for (let i = l, j = r - 1; i < j; i++, j--) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
//Skip to the next word
l = r + 1;
r = l;
}
return arr.join("");
};