leetcode essence of algorithm interview in Dachang 5. Binary search
Video tutorial (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
Binary search
Time complexity O(logn)
Steps:
- Start with the element in the middle of the array. If the element in the middle is exactly the target value, the search ends
- If the target value is greater than or less than the middle element, the search continues on the half of the element greater than or less than the middle element
Code Template
//Binary search pseudo code template
while (left <= right) {
mid = (left + right) / 2;
if (array[mid] === target) return result;
else if (array[mid] < target) left = mid + 1;
else right = mid - 1;
}
704. Binary search (easy)
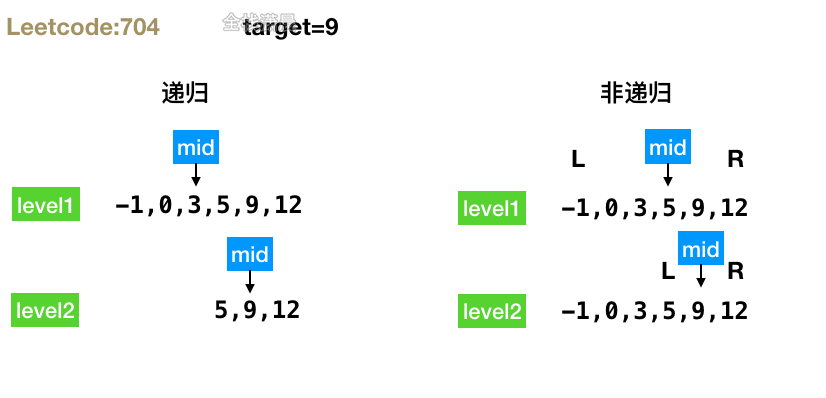
Method 1: recursion
- Idea: first find the middle position and judge whether it is the target value to be searched. If yes, return. If not, judge the size of the target value and the middle element, and then continue to search recursively in the left and right subtrees
- Complexity: time complexity O(logn), space complexity O(logn), recursive stack size
js:
var search = function (nums, target) {
return search_interval(nums, target, 0, nums.length - 1)
};
function search_interval(nums, target, left, right) {
if (left > right) {
return -1
}
let mid = left + Math.floor((right - left) / 2);
if (nums[mid] === target) {//Determine the target value and the size of the intermediate element
return mid
} else if (nums[mid] < target) {//Recursive search for target element
return search_interval(nums, target, mid + 1, right)
} else {
return search_interval(nums, target, left, mid - 1)
}
}
java:
class Solution {
public int search(int[] nums, int target) {
return search_interval(nums, 0, nums.length - 1, target);
}
private int search_interval(int[] nums, int l, int r, int target) {
if (l > r) {
return -1;
}
int mid = l + (r - l) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
return search_interval(nums, l, mid - 1, target);
} else {
return search_interval(nums, mid + 1, r, target);
}
}
}
Method 2: non recursive
- Idea: define the left and right pointers, compare the size of the target element and the middle element, and then continuously narrow the range of the left and right pointers to continue to find the target element
- Complexity: time complexity O(logn), space complexity O(1)
js:
var search = function (nums, target) {
let left = 0,
right = nums.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (nums[mid] === target) {
return mid;
} else if (target < nums[mid]) {//Compare the size of the target and intermediate elements, and then keep narrowing the left and rihgt pointers
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
};
java:
class Solution {
public int search(int[] nums, int target) {
int low = 0, high = nums.length - 1;
while (low <= high) {
int mid = (high - low) / 2 + low;
int num = nums[mid];
if (num == target) {
return mid;
} else if (num > target) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
}
35. Search insertion position (easy)
Time complexity O(logn), space complexity O(1)
js:
var searchInsert = function(nums, target) {
const n = nums.length;
let left = 0, right = n - 1, ans = n;
while (left <= right) {
let mid = ((right - left) >> 1) + left;
if (target <= nums[mid]) {
ans = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return ans;
};
java:
class Solution {
public int searchInsert(int[] nums, int target) {
int n = nums.length;
int left = 0, right = n - 1, ans = n;
while (left <= right) {
int mid = ((right - left) >> 1) + left;
if (target <= nums[mid]) {
ans = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return ans;
}
}
69. Sqrt(x)(easy)
Method 1: dichotomy
- Idea: from 0-x continuous dichotomy to
- Complexity analysis: time complexity O(logx), that is, the number of times required for binary search. Space complexity O(1)
js:
var mySqrt = function (x) {
let left = 0
let right = x
while (left <= right) {
let mid = left + ((right - left) >> 1)//The middle position index x > > 1 is divided by 2 and rounded to narrow the traversal range
if (mid * mid <= x) {
left = mid + 1
} else {
right = mid - 1
}
}
return right
};
Java:
class Solution {
public int mySqrt(int x) {
int left = 0, right = x, ans = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if ((long) mid * mid <= x) {
ans = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return ans;
}
}
Method 2: Newton iteration
- Idea: r = (R + X / R) / 2
- Complexity analysis: time complexity O(logx). Space complexity O(1)
js:
var mySqrt = function(x) {
let r = x
while (r ** 2 > x) r = ((r + x / r) / 2) | 0//Rounding
return r
};
Java:
class Solution {
public int mySqrt(int x) {
if (x <= 1) {
return x;
}
double l = 0;
double r = 1;
while (l != r) {
l = r;
r = (r + x / r) / 2;
}
return (int)r;
}
}
300. Longest increasing subsequence (medium)
The animation is too large. Click to view it
Method 1. Dynamic programming
-
Idea: dp[i] indicates the length of the longest ascending subsequence that selects num [i] and ends with num [i]. Two layer cycle, I: 1 ~ num.length,
j: 0 ~ I, if num [i] > num [J], it forms a rising pair, dp[i] selects the larger one from dp[i], dp[j]+1, and finally returns the total maximum number of dp array
-
Complexity analysis: time complexity O(n^2), n is the length of nums, the outer layer needs to be cycled n times, and dp[i] needs to be from dp[0~i-1], so the complexity is O(n^2). The space complexity is O(n), that is, the space of dp array
js:
const lengthOfLIS = (nums) => {
let dp = Array(nums.length).fill(1);
let result = 1;
for(let i = 1; i < nums.length; i++) {
for(let j = 0; j < i; j++) {
if(nums[i] > nums[j]) {//When num [i] > num [J], a rising pair is formed
dp[i] = Math.max(dp[i], dp[j]+1);//Update dp[i]
}
}
result = Math.max(result, dp[i]);//Update results
}
return result;
};
Java:
class Solution {
public int lengthOfLIS(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
dp[0] = 1;
int result = 1;
for (int i = 1; i < nums.length; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
result = Math.max(result, dp[i]);
}
return result;
}
}
Method 2. Binary search + greed
- Idea: prepare the tail array to store the longest ascending subsequence. The core idea is to put the smaller numbers forward, so that more numbers can be added to the tails array. Add the numbers in nums to the tail continuously. When the element in nums is larger than the last one in the tail, you can rest assured to push into the tail. Otherwise, binary search will be carried out to find the appropriate position for the smaller binary, so that more numbers will form a rising sub sequence with this number
- Complexity: time complexity O(nlogn). N is the length of nums. logn is required for each binary search, so the overall complexity is O(nlogn). The space complexity is O (n), the overhead of tail array
js:
var lengthOfLIS = function (nums) {
let n = nums.length;
if (n <= 1) {
return n;
}
let tail = [nums[0]];//Store the longest ascending subsequence array
for (let i = 0; i < n; i++) {
if (nums[i] > tail[tail.length - 1]) {//When the element in num is larger than the last one in tail, you can safely push into tail
tail.push(nums[i]);
} else {//Otherwise, perform binary search
let left = 0;
let right = tail.length - 1;
while (left < right) {
let mid = (left + right) >> 1;
if (tail[mid] < nums[i]) {
left = mid + 1;
} else {
right = mid;
}
}
tail[left] = nums[i];//Put num [i] in the right place, and the preceding elements are smaller than num [i]
}
}
return tail.length;
};
Java:
class Solution {
private int peek(){
return tail.get(tail.size() - 1);
}
private ArrayList<Integer> tail;
public int lengthOfLIS(int[] nums) {
int len = nums.length;
int last = nums[0];
int max = 1;
tail = new ArrayList<Integer>(len);
tail.add(nums[0]);
for(int i = 1 ; i < len ; ++i){
if( nums[i] > peek() )
tail.add(nums[i]);
else{
int l = 0, r = tail.size() - 1, mid = 0;
while(l <= r){
mid = l + ((r - l) >> 1);
if( nums[i] > tail.get(mid) )
l = mid + 1;
else if( nums[i] < tail.get(mid) )
r = mid - 1;
else {l = mid; break;}
}
tail.set(l, nums[i]);
}
}
return tail.size();
}
}
4. Find the median of two positively ordered arrays (hard)
Method 1. Binary search
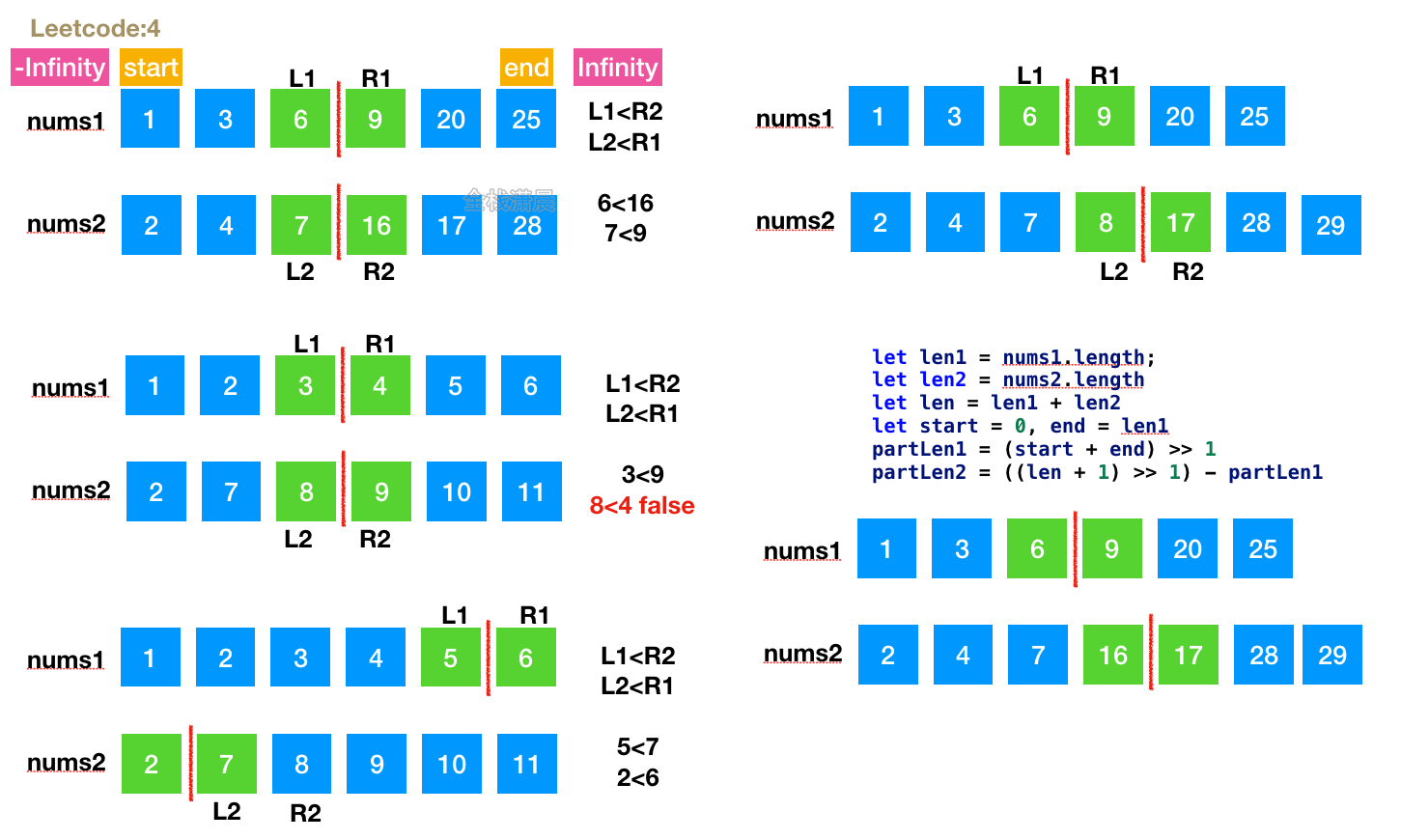
- Idea: after array merging, the sorting complexity is O((m+n) log(m+n)), which does not meet the meaning of the topic. The topic requires O(log (m+n)). As soon as we see the complexity of logn, we associate it with dichotomy. For an array with a smaller bisection length, find the bisection position of the array. Find the bisection position of another array according to the bisection position and the total length of the two arrays. Compare whether the four numbers of the two positions meet the cross less than or equal to. If they do not meet the requirement of continuing bisection, find out if they are satisfied
- Complexity: time complexity O (log (min (m, n)), m and N are the lengths of nums1 and nums2 respectively. The length of each binary loop will be reduced by half, as long as the binary array is relatively short. Space complexity O(1)
Js:
var findMedianSortedArrays = (nums1, nums2) => {
let len1 = nums1.length, len2 = nums2.length
if (len1 > len2) return findMedianSortedArrays(nums2, nums1)//For the smaller binary of nums1 and nums2
let len = len1 + len2//Total length
let start = 0, end = len1 //Start and end positions for dichotomy
let partLen1, partLen2
while (start <= end) {
partLen1 = (start + end) >> 1//nums1 binary position
partLen2 = ((len + 1) >> 1) - partLen1//nums2 binary position
//L1: left position after nums1 two points, L2, right position after nums1 two points
//R1: position on the left after nums2 score, R2: position on the right after nums2 score
//If there are no characters on the left, it is defined as - Infinity, so that all numbers are greater than it. Otherwise, it is one on the left of the binary position of nums1
let L1 = partLen1 === 0 ? -Infinity : nums1[partLen1 - 1]
//If there are no characters on the left, it is defined as - Infinity, so that all numbers are greater than it. Otherwise, it is one on the left of nums2 binary position
let L2 = partLen2 === 0 ? -Infinity : nums2[partLen2 - 1]
//If there is no character on the right, it is defined as Infinity, so that all numbers are less than it, otherwise it is the position of nums1 dichotomy
let R1 = partLen1 === len1 ? Infinity : nums1[partLen1]
//If there is no character on the right, it is defined as Infinity, so that all numbers are less than it, otherwise it is the position of nums1 dichotomy
let R2 = partLen2 === len2 ? Infinity : nums2[partLen2]
if (L1 > R2) {//Non conforming crossing is less than or equal to continue two points
end = partLen1 - 1
} else if (L2 > R1) {//Non conforming crossing is less than or equal to continue two points
start = partLen1 + 1
} else { // L1 < = R2 & & L2 < = R1 meets the cross less than or equal to
return len % 2 === 0 ?
(Math.max(L1, L2) + Math.min(R1, R2)) / 2 : //If the length is an even number, return as half of the sum of the larger one on the left and the smaller one on the right
Math.max(L1, L2) //If the length is an odd number, return it as the larger one on the left
}
}
}
Java:
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
if (nums1.length > nums2.length) {
return findMedianSortedArrays(nums2, nums1);
}
int m = nums1.length;
int n = nums2.length;
int left = 0, right = m;
int median1 = 0, median2 = 0;
while (left <= right) {
int i = (left + right) / 2;
int j = (m + n + 1) / 2 - i;
int nums_im1 = (i == 0 ? Integer.MIN_VALUE : nums1[i - 1]);
int nums_i = (i == m ? Integer.MAX_VALUE : nums1[i]);
int nums_jm1 = (j == 0 ? Integer.MIN_VALUE : nums2[j - 1]);
int nums_j = (j == n ? Integer.MAX_VALUE : nums2[j]);
if (nums_im1 <= nums_j) {
median1 = Math.max(nums_im1, nums_jm1);
median2 = Math.min(nums_i, nums_j);
left = i + 1;
} else {
right = i - 1;
}
}
return (m + n) % 2 == 0 ? (median1 + median2) / 2.0 : median1;
}
}
162. Look for peaks(medium)
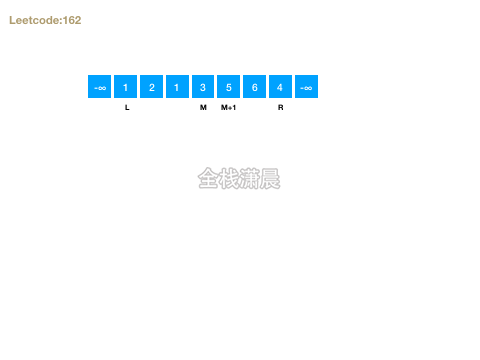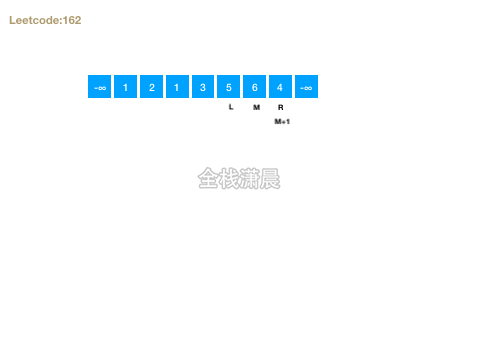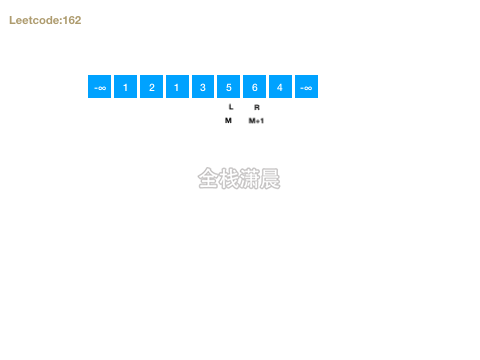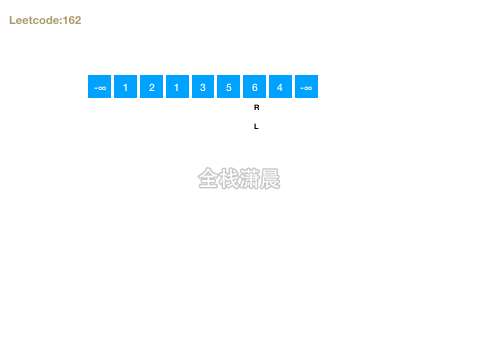
- Train of thought: both num [- 1] and num [n] are - ∞. Therefore, as long as there are two adjacent elements in the array that are increasing, the peak can be found along it
- Complexity: time complexity O(logn), space complexity O(1)
js:
const findPeakElement = nums => {
let [left, right] = [0, nums.length - 1];
while (left < right) {
const mid = left + (right - left) >> 1;//Keep looking for rising element pairs
if (nums[mid] > nums[mid + 1]) {
right = mid;//decline
} else {
left = mid + 1;//rise
}
}
return left;
};
java:
class Solution {
public int findPeakElement(int[] nums) {
int left = 0, right = nums.length - 1;
for (; left < right; ) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1]) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}
74. Search two-dimensional matrix (medium)
- Idea: the matrix satisfies the property of increasing from left to right and from top to bottom, so the two-dimensional array can be regarded as a one-dimensional increasing array, and then binary search can be carried out. Only one coordinate needs to be converted into two-dimensional coordinates.
- Complexity: time complexity O(log(mn)), m, n are the rows and columns of the matrix. In space complexity O(1)
js:
var searchMatrix = function(matrix, target) {
const m = matrix.length, n = matrix[0].length;
let low = 0, high = m * n - 1;
while (low <= high) {
const mid = Math.floor((high - low) / 2) + low;
const x = matrix[Math.floor(mid / n)][mid % n];//Convert one-dimensional coordinates to two-dimensional coordinates
if (x < target) {
low = mid + 1;
} else if (x > target) {
high = mid - 1;
} else {
return true;
}
}
return false;
};
java:
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
int low = 0, high = m * n - 1;
while (low <= high) {
int mid = (high - low) / 2 + low;
int x = matrix[mid / n][mid % n];
if (x < target) {
low = mid + 1;
} else if (x > target) {
high = mid - 1;
} else {
return true;
}
}
return false;
}
}
34. Find the first and last position of an element in a sorted array (medium)
Method 1: first dichotomy, looking for the left and right boundaries
- Idea: binary search, and then try to find the same element to the left and right
- Complexity: time complexity O(n), space complexity O(1)
js:
//nums = [5,7,7,8,8,10], target = 8
var searchRange = function(nums, target) {
let left = 0, right = nums.length - 1, mid;
while (left <= right) {//Binary search target
mid = (left + right) >> 1;
if (nums[mid] === target) break;
if (nums[mid] > target) right = mid - 1;
else left = mid + 1;
}
if(left > right) return [-1, -1];
let i = mid, j = mid;
while(nums[i] === nums[i - 1]) i--;//Try to find the same element to the left
while(nums[j] === nums[j + 1]) j++;//Try to find the same element to the right
return [i, j];
};
java:
class Solution {
public int[] searchRange(int[] nums, int target) {
int leftIdx = binarySearch(nums, target, true);
int rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
return new int[]{leftIdx, rightIdx};
}
return new int[]{-1, -1};
}
public int binarySearch(int[] nums, int target, boolean lower) {
int left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
}
Method 2: modified dichotomy
- Idea: transform the dichotomy and find the starting and ending positions of the target value
- Complexity: time complexity O(logn), space complexity O(1)
js:
//nums = [5,7,7,8,8,10], target = 8
const binarySearch = (nums, target, lower) => {
let left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
var searchRange = function(nums, target) {
let ans = [-1, -1];
const leftIdx = binarySearch(nums, target, true);
const rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] === target && nums[rightIdx] === target) {
ans = [leftIdx, rightIdx];
}
return ans;
};
java:
class Solution {
public int[] searchRange(int[] nums, int target) {
int leftIdx = binarySearch(nums, target, true);
int rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
return new int[]{leftIdx, rightIdx};
}
return new int[]{-1, -1};
}
public int binarySearch(int[] nums, int target, boolean lower) {
int left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
}
153. Find the minimum value in the rotation sort array (medium)
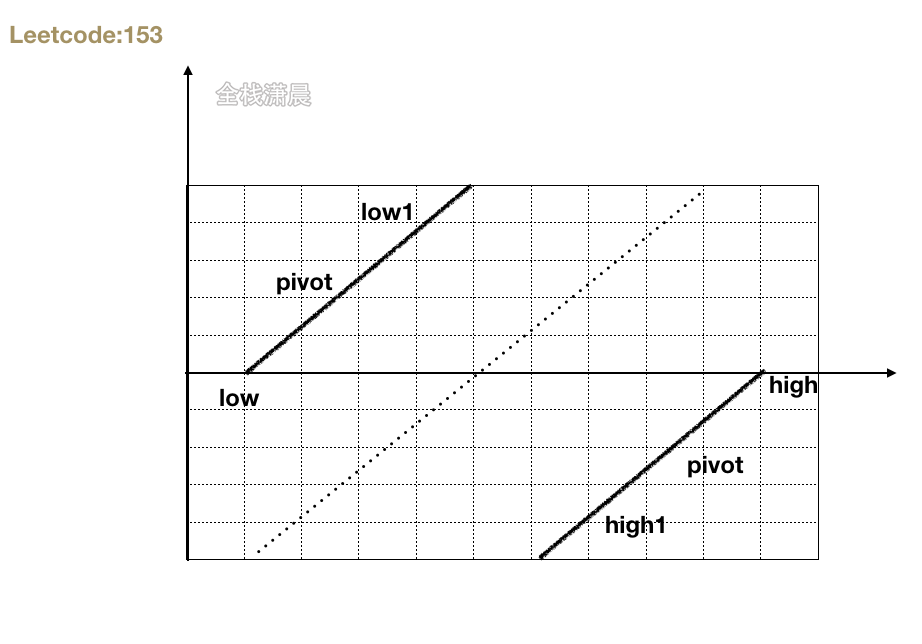
- Idea: the low and high pointers keep moving to the middle and dichotomy. The value of the current node is smaller than that of the high node, so that high is equal to pivot. When the current node ratio is greater than or equal to the high node, let low be equal to pivot+1, and the node that finally meets is the minimum value
- Complexity: time complexity O(logn). Space complexity O(1)
js:
var findMin = function(nums) {
let low = 0;
let high = nums.length - 1;
while (low < high) {
const pivot = low + Math.floor((high - low) / 2);//Intermediate node
if (nums[pivot] < nums[high]) {//The value of the current node is smaller than that of the high node. Let high be equal to pivot
high = pivot;
} else {
low = pivot + 1;//When the current node ratio is greater than or equal to the high node, let low be equal to pivot+1
}
}
return nums[low];//The last node to meet is the minimum
};
java:
class Solution {
public int findMin(int[] nums) {
int low = 0;
int high = nums.length - 1;
while (low < high) {
int pivot = low + (high - low) / 2;
if (nums[pivot] < nums[high]) {
high = pivot;
} else {
low = pivot + 1;
}
}
return nums[low];
}
}
374. Guess the size of the number (easy)
- Complexity: time complexity O(logn). Space complexity O(1)
js:
var guessNumber = function(n) {
let left = 1, right = n;
while (left < right) {
const mid = Math.floor(left + (right - left) / 2);
if (guess(mid) <= 0) {
right = mid; //The update search interval is [left, mid]
} else {
left = mid + 1; //The update search interval is [mid+1, right]
}
}
//left == right is the answer
return left;
};
java:
public class Solution extends GuessGame {
public int guessNumber(int n) {
int left = 1, right = n;
while (left < right) {
int mid = left + (right - left) / 2;
if (guess(mid) <= 0) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}