leetcode essence of algorithm interview in Dachang 13. Monotone stack
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
239. Maximum value of sliding window (hard)
Method 1. Priority queue
The animation is too large. Click to view it
- Idea: for the maximum value problem, we can use the large top heap. Specifically, we maintain a large top heap. Initially, the elements from 0 to k-1 are added to the heap and stored in the key value team of value and index. Then, the sliding window traverses from the element with index K and adds the elements newly entering the sliding window to the heap. When the top element of the heap is not in the sliding window, Keep deleting the top heap elements until the maximum value is in the sliding window.
- Complexity analysis: time complexity O(nlogn). N is the length of nums. The time complexity of adding an element to the priority queue is logn. In the worst case, all elements must join the queue, so the complexity is nlogn. The spatial complexity is O(n). In the worst case, all elements are in the queue, so it is O(n)
js:
class Heap {
constructor(comparator = (a, b) => a - b, data = []) {
this.data = data;
this.comparator = comparator;//comparator
this.heapify();//Heap
}
heapify() {
if (this.size() < 2) return;
for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
this.bubbleDown(i);//bubbleDown operation
}
}
peek() {
if (this.size() === 0) return null;
return this.data[0];//View the top of the heap
}
offer(value) {
this.data.push(value);//Add array
this.bubbleUp(this.size() - 1);//Adjust the position of the added elements in the small top heap
}
poll() {
if (this.size() === 0) {
return null;
}
const result = this.data[0];
const last = this.data.pop();
if (this.size() !== 0) {
this.data[0] = last;//Swap the first and last elements
this.bubbleDown(0);//bubbleDown operation
}
return result;
}
bubbleUp(index) {
while (index > 0) {
const parentIndex = (index - 1) >> 1;//Location of parent node
//If the current element is smaller than the element of the parent node, the positions of the current node and the parent node are exchanged
if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
this.swap(index, parentIndex);//Swap the location of yourself and the parent node
index = parentIndex;//Continuously take up the parent node for comparison
} else {
break;//If the current element is larger than the element of the parent node, it does not need to be processed
}
}
}
bubbleDown(index) {
const lastIndex = this.size() - 1;//Location of the last node
while (true) {
const leftIndex = index * 2 + 1;//Location of left node
const rightIndex = index * 2 + 2;//Location of the right node
let findIndex = index;//Location of the bubbleDown node
//Find the node with small value in the left and right nodes
if (
leftIndex <= lastIndex &&
this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
) {
findIndex = leftIndex;
}
if (
rightIndex <= lastIndex &&
this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
) {
findIndex = rightIndex;
}
if (index !== findIndex) {
this.swap(index, findIndex);//Swap the current element and the small value in the left and right nodes
index = findIndex;
} else {
break;
}
}
}
swap(index1, index2) {//Swap the positions of the two elements in the heap
[this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
}
size() {
return this.data.length;
}
}
var maxSlidingWindow = function(nums, k) {
let ans = [];
let heap = new Heap((a, b) => b.val - a.val);//Large top reactor
for(let i=0;i<k-1;i++) heap.offer({val: nums[i], index: i});//Initially, 0 ~ k-1 elements are added to the heap
for(let i=k-1; i<nums.length; i++){//The sliding window traverses from the element with index k-1
heap.offer({val: nums[i], index: i});//Add the elements newly entered into the sliding window to the heap
//When the heap top element is not in the sliding window, delete the heap top element continuously until the maximum value is in the sliding window.
while(heap.peek().index<=i-k) heap.poll();
ans.push(heap.peek().val);//Add the maximum value in the sliding window to ans
}
return ans;
}java:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {//Large top reactor
public int compare(int[] pair1, int[] pair2) {
return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
}
});
for (int i = 0; i < k; ++i) {//Initially, 0 ~ k-1 elements are added to the heap
pq.offer(new int[]{nums[i], i});
}
int[] ans = new int[n - k + 1];
ans[0] = pq.peek()[0];//Initial maximum value of sliding window
for (int i = k; i < n; ++i) {//The sliding window traverses from the element with index k
pq.offer(new int[]{nums[i], i});//Add the elements newly entered into the sliding window to the heap
//When the heap top element is not in the sliding window, delete the heap top element continuously until the maximum value is in the sliding window.
while (pq.peek()[1] <= i - k) {
pq.poll();
}
ans[i - k + 1] = pq.peek()[0];//Add the maximum value in the sliding window to ans
}
return ans;
}
}Method 2. Monotone queue
The animation is too large. Click to view it
- Idea: maintain the monotonically decreasing queue. When the element entering the sliding window is greater than or equal to the element at the end of the queue, keep leaving the queue from the end of the queue until the element entering the sliding window is less than the element at the end of the queue, so as to ensure the monotonically decreasing nature. When the element at the head of the queue is already outside the sliding window, remove the opposite element. When i is greater than or equal to k-1, Monotonically decreasing queue head is the maximum value of sliding window
- Complexity analysis: time complexity O(n), n is the length of nums, and each element is queued once. The spatial complexity is O(k), and the queue can store up to k-sized elements
js:
var maxSlidingWindow = function (nums, k) {
const q = [];//Single decreasing double ended queue
const ans = [];//Final return result
for (let i = 0; i < nums.length; i++) {//Cyclic nums
//When the element entering the sliding window is greater than or equal to the element at the end of the team, it will continue to leave the team at the end of the team,
//Until the element entering the sliding window is smaller than the element at the end of the queue, the monotonic decreasing property is guaranteed
while (q.length && nums[i] >= nums[q[q.length - 1]]) {
q.pop();
}
q.push(i);//The index of the element is queued
while (q[0] <= i - k) {//The team header element is already outside the sliding window. Remove the header element
q.shift();
}
//When i is greater than or equal to k-1, monotonically decreasing queue head is the maximum value of sliding window
if (i >= k - 1) ans.push(nums[q[0]]);
}
return ans;
};Java:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
Deque<Integer> deque = new LinkedList<Integer>();
for (int i = 0; i < k; ++i) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
}
int[] ans = new int[n - k + 1];
ans[0] = nums[deque.peekFirst()];
for (int i = k; i < n; ++i) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
while (deque.peekFirst() <= i - k) {
deque.pollFirst();
}
ans[i - k + 1] = nums[deque.peekFirst()];
}
return ans;
}
}84. The largest rectangle in the histogram (hard)
- Idea: prepare to monotonically increase the stack to store the array subscript, because in this way, you can find the first subscript smaller than yourself on the left from the top of the stack. In this way, starting from the current subscript to the first column smaller than yourself, the subscript is the width of the rectangular area, and then multiplying the height of the current column is the area. If the current column is greater than the height of the column corresponding to the subscript on the top of the stack, enter the stack, Otherwise, keep coming out of the stack, calculate the rectangular area that can be formed by the column at the top of the stack, and then update the maximum rectangular area
- Complexity: time complexity O(n). N is the length of heights. Each element in the array should be out of the stack once. Space complexity O(n), stack space up to n
The animation is too large. Click to view it
js:
const largestRectangleArea = (heights) => {
let maxArea = 0
const stack = [] //Monotonically increasing stack, pay attention to the time subscript of stack storage
heights = [0, ...heights, 0] //Add two sentinels before and after the heights array to clear the elements in the monotonically increasing stack
for (let i = 0; i < heights.length; i++) {
//When the height corresponding to the current element is less than the height corresponding to the top element of the stack
while (heights[i] < heights[stack[stack.length - 1]]) {
const stackTopIndex = stack.pop() //Out of stack
maxArea = Math.max( //Calculate the area and update the maximum area
maxArea,
heights[stackTopIndex] * (i - stack[stack.length - 1] - 1)//Gao Chengkuan
)
}
stack.push(i)//Add current subscript to stack
}
return maxArea
}java:
class Solution {
public int largestRectangleArea(int[] heights) {
Stack<Integer> stack = new Stack<>();
int len = heights.length;
int maxArea = 0;
for(int i = 0; i < len; i++){
if(stack.isEmpty() || heights[stack.peek()] <= heights[i])
stack.push(i);
else{
int top = -1;
while(!stack.isEmpty() && heights[stack.peek()] > heights[i])
{
top = stack.pop();
maxArea = Math.max(maxArea, heights[top] * (i - top));
}
heights[top] = heights[i];
stack.push(top);
}
}
while(!stack.isEmpty())
{
int top = stack.pop();
maxArea = Math.max(maxArea, (len - top) * heights[top]);
}
return maxArea;
}
}85. Maximum rectangle (hard)
Method 1. Monotone stack
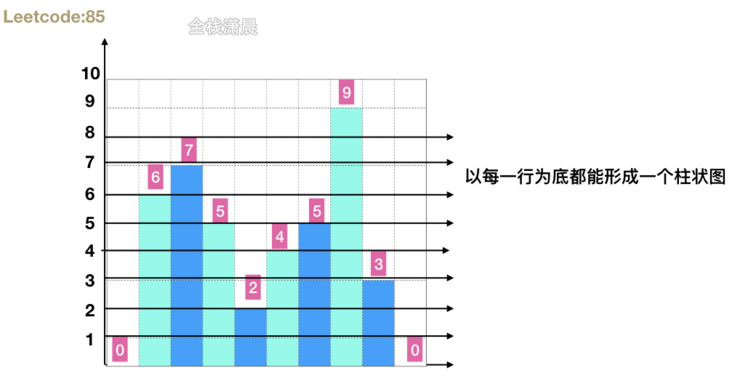
- Idea: a variant of question 84. The histogram formed from the first line to the nth line can be solved by question 84, and then cycle each line to calculate the maximum area of the histogram at the bottom of this line, and then update the maximum rectangular area
- Complexity: time complexity O(mn), m and N are the height and width of the rectangle respectively. Cycle M rows, and cycle the height of each column in each row. Space complexity O(n), the space of the heights array.
js:
var maximalRectangle = function (matrix) {
if (matrix.length == 0) return 0;
let res = 0;
let heights = new Array(matrix[0].length).fill(0);//Initializes the heights array
for (let row = 0; row < matrix.length; row++) {
for (let col = 0; col < matrix[0].length; col++) {
if(matrix[row][col] == '1' ) heights[col] += 1;
else heights[col] = 0;
}//Find the heights [] of each layer and pass it to the function of question 84
res = Math.max(res, largestRectangleArea(heights));//Update the maximum rectangular area
}
return res;
};
const largestRectangleArea = (heights) => {
let maxArea = 0
const stack = [] //Monotonically increasing stack, pay attention to the time subscript of stack storage
heights = [0, ...heights, 0] //Add two sentinels before and after the heights array to clear the elements in the monotonically increasing stack
for (let i = 0; i < heights.length; i++) {
//When the height corresponding to the current element is less than the height corresponding to the top element of the stack
while (heights[i] < heights[stack[stack.length - 1]]) {
const stackTopIndex = stack.pop() //Out of stack
maxArea = Math.max( //Calculate the area and update the maximum area
maxArea,
heights[stackTopIndex] * (i - stack[stack.length - 1] - 1)//Gao Chengkuan
)
}
stack.push(i)//Add current subscript to stack
}
return maxArea
}java:
class Solution {
public int maximalRectangle(char[][] matrix) {
int row = matrix.length;
if (row == 0)
return 0;
int col = matrix[0].length;
int[] heights = new int[col + 1];
heights[col] = -1;
int res = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
heights[j] = matrix[i][j] == '1' ? heights[j] + matrix[i][j] - '0' : 0;
}
res = Math.max(res, largestRectangleArea(Arrays.copyOf(heights, col + 1)));
}
return res;
}
public int largestRectangleArea(int[] heights) {
Stack<Integer> stack = new Stack<>();
int len = heights.length;
int maxArea = 0;
for (int i = 0; i < len; i++) {
if (stack.isEmpty() || heights[stack.peek()] <= heights[i])
stack.push(i);
else {
int top = -1;
while (!stack.isEmpty() && heights[stack.peek()] > heights[i]) {
top = stack.pop();
maxArea = Math.max(maxArea, heights[top] * (i - top));
}
heights[top] = heights[i];
stack.push(top);
}
}
return maxArea;
}
}496. Next larger element I (easy)
The animation is too large. Click to view it
Idea:
- Loop nums2. If the element of the loop is larger than the element at the top of the stack and the stack is not empty, the element at the top of the stack is continuously added to the map as a key and the current element as a value
- The essence is that the first value larger than the top element of the stack will keep the elements in the stack out of the queue, so this number is the next larger number of these out of the stack elements
- The remaining elements do not find the maximum value
- Traverse nums1 and push the result into ans
- Complexity: the time complexity is O(m+n), nums1 and nums2 are traversed, and the elements in nums2 are in and out of the queue once. Space complexity O(n), stack space and map space complexity
js:
let nextGreaterElement = function(nums1, nums2) {
let map = new Map(), stack = [], ans = [];
//Loop nums2. If the element of the loop is larger than the element at the top of the stack and the stack is not empty, the element at the top of the stack is continuously added to the map as a key and the current element as a value
//The essence is that the first value larger than the top element of the stack will keep the elements in the stack out of the queue, so this number is the next larger number of these out of the stack elements
nums2.forEach(item => {
while(stack.length && item > stack[stack.length-1]){
map.set(stack.pop(), item)
};
stack.push(item);
});
stack.forEach(item => map.set(item, -1));//The remaining elements do not find the maximum value
nums1.forEach(item => ans.push(map.get(item)));//Traverse nums1 and push the result into ans
return ans;
};java:
public class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
Deque<Integer> stack = new ArrayDeque<>();
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < len2; i++) {
while (!stack.isEmpty() && stack.peekLast() < nums2[i]) {
map.put(stack.removeLast(), nums2[i]);
}
stack.addLast(nums2[i]);
}
int[] ans = new int[len1];
for (int i = 0; i < len1; i++) {
ans[i] = map.getOrDefault(nums1[i], -1);
}
return ans;
}
}
42. Rainwater connection (hard)
Idea: first consider the violent method and find the idea. The violent method can traverse the array, find the maximum height in the left column and the maximum height in the right column on both sides of each position, and then subtract the height of the current column from the smaller of the left and right maximum heights, which is the amount of water that the current position can receive. This method needs to loop the whole array, and each position needs to traverse the array to find the maximum height of the left and right columns. It nested a loop, so the complexity is O(n^2).
How can we speed up the nested cycle? In fact, we can pre calculate the maximum height array from left to right and from right to left. When cycling the array, we can directly get the maximum height on the left and right sides of the position. The water receiving capacity of the current position is the smaller of the height on the left and right sides minus the height of the column in the current position
- Complexity: time complexity O(n), find the maximum height on the left and right, and cycle to calculate the water intake at each position. There are 3 cycles in total, but they are not nested. The space complexity is O(n), and N is the heights array. leftMax and rightMax arrays are used, that is, the array storing the maximum height on the left and right sides.
Method 1. Dynamic programming
The animation is too large. Click to view it
js:
var trap = function(height) {
const n = height.length;
if (n == 0) {//Extreme situation
return 0;
}
const leftMax = new Array(n).fill(0);//Initializes the array of maximum values viewed from left to right
leftMax[0] = height[0];
for (let i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
const rightMax = new Array(n).fill(0);//Initializes the array of maximum values viewed from right to left
rightMax[n - 1] = height[n - 1];
for (let i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
let ans = 0;
//Loop array. The amount of rainwater that can be received at each position is the smaller of the maximum value around this position minus the current height
for (let i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
};java:
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int[] leftMax = new int[n];
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
int[] rightMax = new int[n];
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
}Method 2: monotone stack
The animation is too large. Click to view it
- Idea: traverse the heights array and add the elements to the monotonically decreasing stack. If the height of the current column is greater than the height of the column at the top of the stack, keep coming out of the stack, which is equivalent to finding the position on the left lower than the current column, and then accumulate the area after each coming out of the stack.
- Complexity: time complexity O(n). N is the length of heights. Each element in the array can be put on and out of the stack at most once. The space complexity O(n), the space of the stack, will not exceed the length of heights at most
js:
var trap = function(height) {
let ans = 0;
const stack = [];//Monotonically decreasing stack. It stores subscripts
const n = height.length;
for (let i = 0; i < n; ++i) {//Circular heights
//The height of the current column is higher than that of the column at the top of the stack
while (stack.length && height[i] > height[stack[stack.length - 1]]) {
const top = stack.pop();
if (!stack.length) {//Jump out of loop when stack is empty
break;
}
const left = stack[stack.length - 1];//Get the position lower than the current column on the left of the current position
const currWidth = i - left - 1;//Calculated width
const currHeight = Math.min(height[left], height[i]) - height[top];//Calculated height
ans += currWidth * currHeight;//Calculate the current area
}
stack.push(i);//Add stack
}
return ans;
};java:
class Solution {
public int trap(int[] height) {
int ans = 0;
Deque<Integer> stack = new LinkedList<Integer>();
int n = height.length;
for (int i = 0; i < n; ++i) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop();
if (stack.isEmpty()) {
break;
}
int left = stack.peek();
int currWidth = i - left - 1;
int currHeight = Math.min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stack.push(i);
}
return ans;
}
}Method 3. Double pointer
The animation is too large. Click to view it
- Idea: if there is a column higher than the current height on the right, a depression will be formed. Similarly, if there is a column higher than the current height on the left, a pit will also be formed. Use the double pointer to cycle the heights array to judge whether a depression is formed. If a depression can be formed, calculate the accumulated water and add it to ans.
- Complexity: the time complexity O(n), where n is the length of heights, traversing heights once in total. Spatial complexity O(1), only two pointers are used
js:
var trap = function(height) {
let ans = 0;
let left = 0, right = height.length - 1;//Initialize double pointer
let leftMax = 0, rightMax = 0;//Maximum height of left and right sides
while (left < right) {//Circular double pointer
leftMax = Math.max(leftMax, height[left]);//Left maximum
rightMax = Math.max(rightMax, height[right]);//Right maximum
if (height[left] < height[right]) {//The column on the right is higher than the column on the left. Calculate the cumulative result of water connection at this position
ans += leftMax - height[left];
++left;
} else { //The column on the left is higher than or equal to the column on the right. Calculate the cumulative result of water connection at this position
ans += rightMax - height[right];
--right;
}
}
return ans;
};java:
class Solution {
public int trap(int[] height) {
int ans = 0;
int left = 0, right = height.length - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
}