The topics are as follows:
Give you a matrix of m x n, where the values are non negative integers, representing the height of each cell in the two-dimensional height map. Please calculate the maximum volume of rainwater that can be received by the shape in the map.

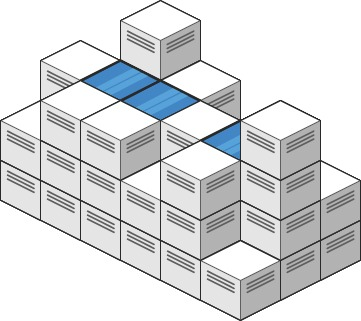
Input: hightmap = [[1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1]]
Output: 4
Explanation: after the rain, the rain will be in the blue box above. The total amount of rainwater is 1 + 2 + 1 = 4.

analysis:

This topic is a classic topic. The principle and method of solving the problem can refer to "receiving rain". This topic has changed from one-dimensional array to two-dimensional array.
First, let's think about what kind of box can catch water:

The box is not the outermost box;
The height of the block itself is lower than that of the four adjacent blocks above, below, left and right after receiving water;
We assume that the index of the block is (i,j), the height of the block is highmap [i] [J], and the height of the block after receiving water is water[i][j]. Then we know that the height of block (i,j) after water connection is:

water[i][j]=max(heightMap[i][j],min(water[i−1][j],water[i+1][j],water[i][j−1],water[i][j+1]))

We know that the calculation formula of the actual water receiving capacity of block (i,j)(i,j) is water[i][j] − hightmap [i] [J].
First, we can determine that the height of the outermost block of the matrix after receiving water is the height of the block itself. Because the outermost block cannot receive water, the outermost block water [i] [J] = highmap [i] [J].

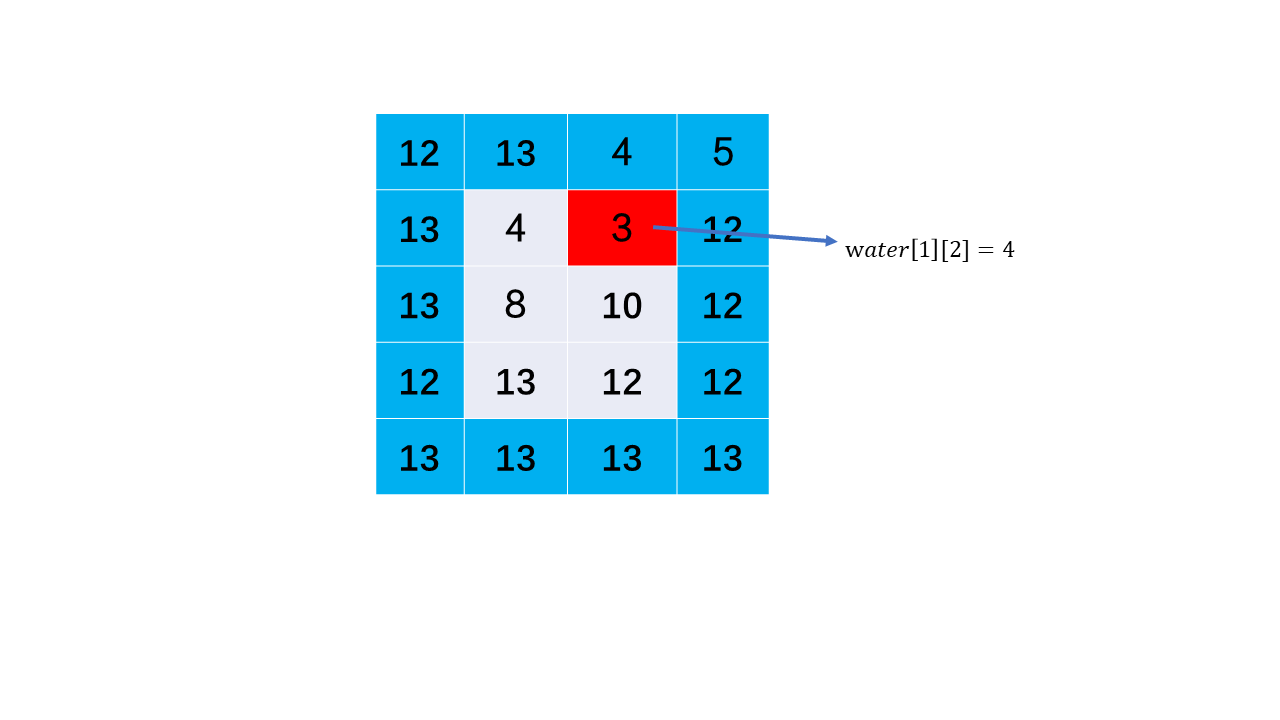
According to the principle of short board, the height of rainwater received is determined by the shortest board around the container. We can know that the height of the water in the container depends on the lowest square in the outermost layer.

Assuming that we have known the minimum value of the water receiving height of the outermost block, we can certainly determine the water receiving height of the adjacent blocks of the minimum height block according to the barrel principle. At the same time, we update the mark of the outermost box. We find the minimum value of the height after water connection again in the new outermost box, and determine the water connection height of its adjacent box,

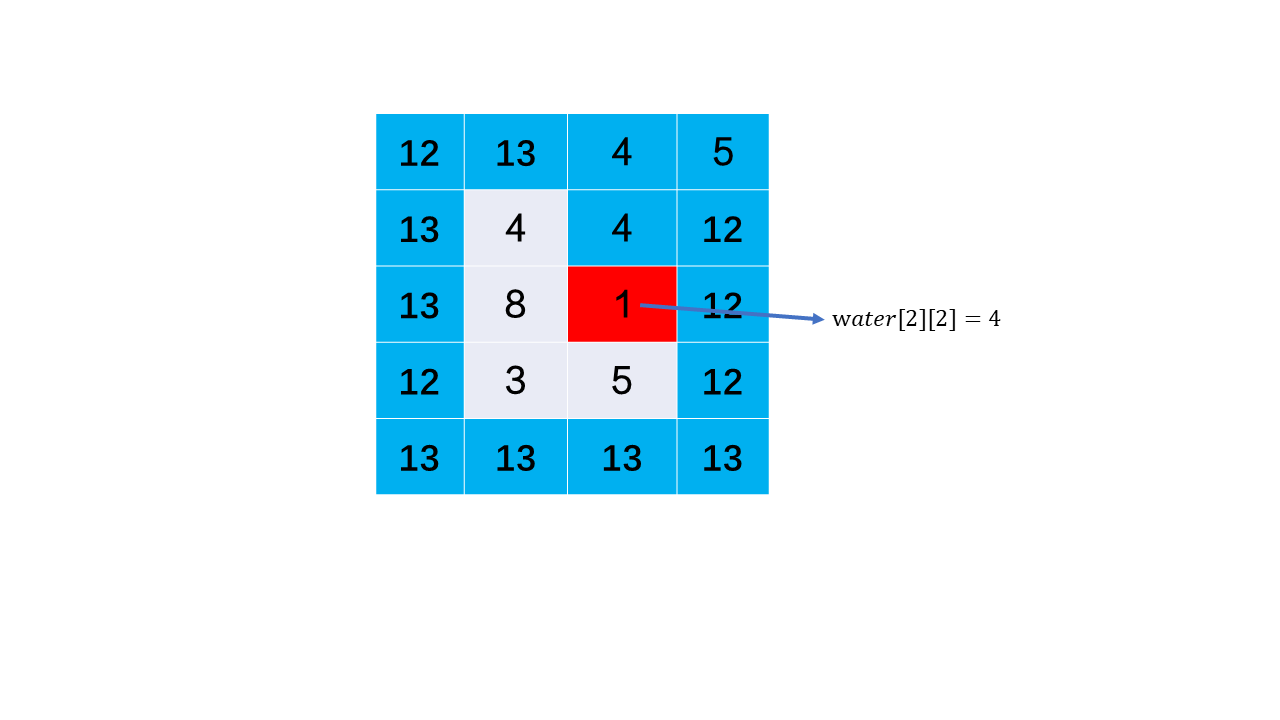
Then update the outermost layer again and iterate successively until the water receiving height of all blocks is calculated, so as to know the water receiving capacity in the matrix.
The code is as follows:

class Solution {
    public int trapRainWater(int[][] heightMap) {
 if (heightMap.length <= 2 || heightMap[0].length <= 2) {
            return 0;
        }
        int m = heightMap.length;
        int n = heightMap[0].length;
        // Visited nodes
        boolean[][] visit = new boolean[m][n];
        // Small top heap, and put in an array, compare the height
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    // i * n + j represents the number of
                    // 0    1   2    //4*3d
                    // 3    4   5
                    // 6    7   8
                    // 9    10  11
                    pq.offer(new int[]{i * n + j, heightMap[i][j]});
                    visit[i][j] = true;
                }
            }
        }
        int res = 0;
        // Through the for cycle for 4 times, i and i+1 can be used to locate [up, right, down, left]
        int[] dirs = {-1, 0, 1, 0, -1};
        // If the small top pile is empty
        while (!pq.isEmpty()) {
            // Small top stack
            int[] curr = pq.poll();
            for (int k = 0; k < 4; ++k) {
                // The number of fetching positions, / N is the number of rows index, and% n is the number of columns index
                int nx = curr[0] / n + dirs[k];
                int ny = curr[0] % n + dirs[k + 1];
                // No cross-border and never visited
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && !visit[nx][ny]) {
                    // If the current position is larger than the surrounding area, water can be injected, and the height after access is the height after water injection ※ because this starts from the minimum, and if it is smaller than the minimum, rainwater can be received
                    if (curr[1] > heightMap[nx][ny]) {
                        res += curr[1] - heightMap[nx][ny];
                        pq.offer(new int[]{nx * n + ny, curr[1]});
                    } else { // Update boundary if greater than
                        pq.offer(new int[]{nx * n + ny,heightMap[nx][ny]});
                    }
                    // Set the visited location to true
                    visit[nx][ny] = true;
                }
            }
        }
        return res;
    }
}