leetcode circular linked list I & II

Keywords: data structure leetcode linked list

1. Circular linked list I

1.1 Title Description

The link to this question comes from leetcode

Example

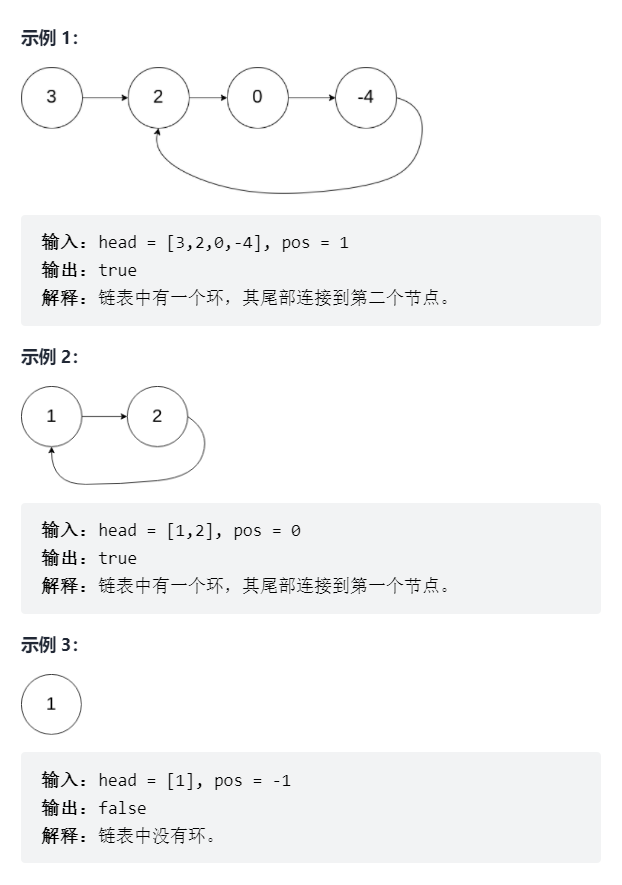
Advanced and tips:

1.1.1 interface function

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    
}

1.2 general framework

1.2.1 ideas

First, we should find out what is a linked list, that is, the tail of the original list may point to any node containing itself

The method is to use the fast and slow pointer. As long as it is a ring, as long as there is a fast pointer and a slow pointer, they will always meet at a certain point

1.2.2 specific steps

Implement a fast and slow pointer and put it into the loop. As long as it is equal, it means it is a ring

  while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        return true;
    }

1.3 overall realization

bool hasCycle(struct ListNode *head) {
    struct ListNode*slow=head,*fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        return true;
    }
    return false;
}

Summary:

This problem is only a preliminary stage, so it is easy to solve

But how would you answer the following three questions?

No, when slow enters the ring, it is essentially a catch-up problem. The distance between fast and slow should be smaller and smaller
Not necessarily. It's essentially the same logic as the first question
To sum up, when fast takes three steps at a time, if the gap N between slow and fast is odd when slow enters the loop, and the length of the loop is even, then it will never catch up

Therefore, we can't set the speed of fast arbitrarily

Since the fast pointer travels twice as far as the slow pointer, there is an equation:
2 ∗ ( L + X ) = L + C + X 2*(L+X)=L+C+X 2∗(L+X)=L+C+X
However, this inference is wrong because we ignore the possibility of fast pointer

Yes, slow can only walk within one circle, and fast will catch up with slow, so the distance of slow is L+X

However, fast doesn't have to take only one lap. It's entirely possible that it took N laps in it, so the fast pointer should have gone
2 ∗ ( L + X ) = L + N ∗ C + X 2*(L+X)=L+N*C+X 2∗(L+X)=L+N∗C+X
So after simplifying the equation, it should be
L = N ∗ C − X L=N*C-X L=N∗C−X {N*C-X}

From the previous conclusion, we will have ideas for the following upgraded title

2. Circular linked list II

The link to this question comes from leetcode

2.1 Title Description

Example

Advanced and tips

2.1.1 interface function

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    
}

2.2 method I

The idea of method 1 inherits the idea of the third problem before. In essence, the method is difficult to think of, but the code is simple

2.2.1 specific steps

Due to the previously given formula
L = N ∗ C − X L=N*C-X L=N∗C−X {N*C-X}
Therefore, it can be proved by inference that if I call the fast pointer position of the meeting point meet, and there is a head pointer head, one of the two pointers will go L from head and the other will go N*C-X from meet, they will meet at the entry point, just to find the position of the entry point

2.2.2 overall realization

 struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow=head,*fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            //meet
             struct ListNode*meet=fast;
             //Prove by inference that a pointer
             while(meet!=head)
            {
                meet=meet->next;
                head=head->next;
            }
            return meet;
        }
    }
    return NULL;
}

2.3 method II

Compared with method 1, method 2 has simple idea but complex code

2.3.1 ideas and ideas

First, the fast and slow pointers meet, and then we empty the meeting point to create a newhead node. Then, if we go with head, it will be transformed into the intersection problem we have done before, so as to find out the intersection point, which is what we require

Intersection of linked lists

This method is not written here