384. Medium difficulty:

Method 1: Violence: time complexity O(n^2) space complexity O(n)

Topic meaning: the topic requires us to implement a constructor and two methods of the Solution class
1. Solution(int[] nums) initializes the object with an integer array nums

// Title passed in array nums
public Solution(int[] nums) {
    // Array and nums point to the same array. Using array is conducive to calling between methods
    array = nums;
    // Clone the incoming array as a backup for reset
    original = nums.clone();
}

2. int[] reset() resets the array to its initial state and returns:
This involves the method of assignment between arrays and their respective effects:
(1) Direct array = original; Although all elements of array are equal to original, the change of one of them will change both, that is, the two arrays are equal
(2) Use the clone method: for arrays of basic data types:
One dimensional array: deep cloning; (reallocate space and copy elements)
2D arrays: shallow clones. (pass references only)

public int[] reset() { 
    // array is applicable to arrays that are out of order. Pass the backup original to it
    array = original;
    // After the reset() method is called, the original array will also become the initial state,
    // Therefore, assign original to array. At this point, array and original point to the same array,
    // The next time you shuffle (), the original will change due to the change of array, so now clone() to reallocate space for the original
    // Being a separate array is not affected by array
    original = original.clone();
    return array;
}

3. int[] shuffle() returns the result of random array scrambling:
List list = new ArrayLIst(); ArrayList = new arraylist(); Differences between:
If you need to modify the ArrayList to LinkedList or other in the future, you just need to make the following simple modifications:
Set list = new arraylist(); Change to list = new linkedlist();
ArrayList is the implementation of variable array of List interface, a kind of polymorphic form
The Java.util.ArrayList class is a dynamic array type. ArrayList objects have the characteristics of both arrays and linked lists. You can add or delete an element from the linked List at any time. ArrayList implements the List interface
When we don't know how many data elements there are, we can use ArrayList; If you know how many elements there are in a data set, use an array

private List<Integer> getArrayCopy() {
    // Create an ArrayList dynamic array to receive the elements in the array
    List<Integer> asList = new ArrayList<Integer>();
    // Cyclic assignment
    for (int i = 0; i < array.length; i++) {
        asList.add(array[i]);
    }
    // The returned array has the same elements as array
    return asList;
}

public int[] shuffle() {
    // Call the getArrayCopy method to get the same array as the array element
    List<Integer> aux = getArrayCopy();
	// Re assign values to the array one by one from the subscript 0, that is, disrupt the nums array
    for (int i = 0; i < array.length; i++) {
        // Randomly generate a number less than the length of the aux array (it can be regarded as randomly generating a valid array element subscript)
        int removeIdx = rand.nextInt(aux.size());
        // Assign a value to array
        array[i] = aux.get(removeIdx);
        // Remove the random subscripts that have been selected to avoid being selected again, which is also the reason for using the dynamic array ArrayList
        aux.remove(removeIdx);
    }

    return array;
}

Full code:

/**
 * Your Solution object will be instantiated and called as such:
 * Your solution object will be instantiated and called in this way
 * Solution obj = new Solution(nums);
 * int[] param_1 = obj.reset();
 * int[] param_2 = obj.shuffle();
 */
class Solution {
    private int[] array;
    private int[] original;
	// The rand object is used to create random numbers of the type and range we specify
    private Random rand = new Random();

    private List<Integer> getArrayCopy() {
        List<Integer> asList = new ArrayList<Integer>();
        for (int i = 0; i < array.length; i++) {
            asList.add(array[i]);
        }
        return asList;
    }

    public Solution(int[] nums) {
        array = nums;
        original = nums.clone();
    }
    
    public int[] reset() {
        array = original;
        original = original.clone();
        return array;
    }
    
    public int[] shuffle() {
        List<Integer> aux = getArrayCopy();

        for (int i = 0; i < array.length; i++) {
            int removeIdx = rand.nextInt(aux.size());
            array[i] = aux.get(removeIdx);
            aux.remove(removeIdx);
        }

        return array;
    }
}

Method 2: Fisher Yates shuffle algorithm: spatio-temporal complexity: O(N)

For the shuffle problem, Fisher Yates shuffle algorithm is not only a popular solution, but also an asymptotic optimal solution.

Principle:
General idea: we can use a simple technique to reduce the time complexity and space complexity of the previous algorithm, that is to exchange the elements in the array with each other, so as to avoid the time used to modify the list in each iteration.

Algorithm implementation: Fisher Yates shuffle algorithm is very similar to violence algorithm. In each iteration, a random integer ranging from the current subscript to the subscript of the element at the end of the array is generated. Next, exchange the current element with the element referred to by the randomly selected subscript. This step simulates the process of touching an element from the "hat" every time. The basis for selecting the subscript range is that each touched element can no longer be touched
(that is, start traversing from subscript 0. Each time we traverse an item, we randomly select one of the subscripts from the current subscript to the end of the array, exchange the values, and then traverse the next item. At this time, the selected random element has become the previous item of the current traversal item, and we select the random number from the current item, which realizes that the touched element will not be touched again.)

Details to note: the current element can be exchanged with itself, otherwise the probability of generating the final permutation and combination will be wrong
(in order to make each permutation of the array as equal as possible, there are some other things to pay attention to. For example, an array with length n has n! Different permutation combinations. Therefore, in order to encode all permutations in the integer space, we need lg(n!) Bit, which is not guaranteed by the default pseudo-random number. Therefore, every time we select a random element, we must treat all the elements that have not been selected as optional items, and the currently traversed items also belong to them, so they can be exchanged with each other.)

class Solution {
    // Member attributes: this part is the same as violence
    private int[] array;
    private int[] original;

    Random rand = new Random();
	
    // The parameter is an optional interval of random subscripts that have not been selected
    private int randRange(int min, int max) {
        // Generate a random number less than max - min, and then add min to return to return a value between the current item and the last item 
        return rand.nextInt(max - min) + min;
    }
	
    // Parameter i is the currently traversed subscript, and parameter j is the randomly selected subscript
    // Simple interchange value operation
    private void swapAt(int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
	
    // Constructor: initializes the object using the integer array nums, which is the same as violence
    public Solution(int[] nums) {
        array = nums;
        original = nums.clone();
    }
    
    // Reset the array back to its original state, which is the same as violence
    public int[] reset() {
        array = original;
        original = original.clone();
        return original;
    }
    
    // Scramble array
    public int[] shuffle() {
        for (int i = 0; i < array.length; i++) {
            // Compared with violence, the swapAt method is used to exchange the elements in the array with each other, eliminating the time spent on modifying the additional array
            // swapAt passes in two parameters: current subscript and random subscript
            // randRange passes in the current subscript and the total length of the array
            swapAt(i, randRange(i, array.length));
        }
        return array;
    }
}

198. Medium difficulty:

Note:
If you only look at the examples given, you will think that there are only two possibilities for stealing: stealing or not stealing on the first day, not stealing or stealing on the second day
However, there are some cases, such as array [2,1,1,2]. We choose to steal on the first day and not steal on the next two days, and then steal on the last day, so as to reach the maximum amount. This is different from the above two possibilities.

Method 1: dynamic programming

Code principle: selected from:

Author: nettee
Link: https://leetcode-cn.com/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/

The four problem solving steps of dynamic programming are:
1. Define subproblems
2. Write the recurrence relation of the subproblem
3. Determine the calculation order of DP array
4. Space optimization (optional)

To 1: dynamic programming has a definition of "sub problem". Subproblem: subproblem is similar to the original problem, but smaller.
For example, in this thief problem, the original problem is "the maximum amount that can be stolen from all houses", which reduces the scale of the problem. The sub problem is "the maximum amount that can be stolen from K houses", expressed by f(k).

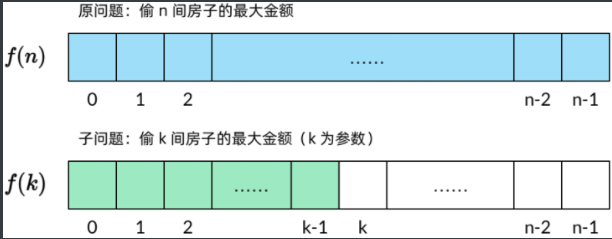
The subproblem is parameterized. The subproblem we define has parameter k. Suppose there are n houses, there are n sub problems. In fact, dynamic programming is to find the solution of the original problem by finding the solution of this pile of subproblems. This requires that the subproblem should have two properties:
(1) The original problem should be represented by a subproblem. For example, in this thief problem, when k=n is actually the original problem.
(2) The solution of one subproblem can be obtained by the solution of other subproblems. For example, in this thief problem, f(k) can be solved by f(k-1) and f(k-2). The specific principle will be explained later. This property is what textbooks call "optimal substructure". If such a subproblem cannot be defined, the problem can not be solved by dynamic programming.
Because the thief problem is relatively simple, the definition of sub problem is actually very intuitive. Some difficult dynamic programming problems may require some skills to define subproblems.

Pair 2: this step is the most critical step to solve the dynamic programming problem. However, this step is also the one that cannot be reflected in the code
Recurrence relation of the problem: suppose there are n houses in total, and the amount of each house is H0, H1,..., Hn-1 respectively. Sub problem f(k) represents the maximum amount that can be stolen from the previous K houses (i.e. H0, H1,..., Hk-1). Well, there are two ways to steal k a house:

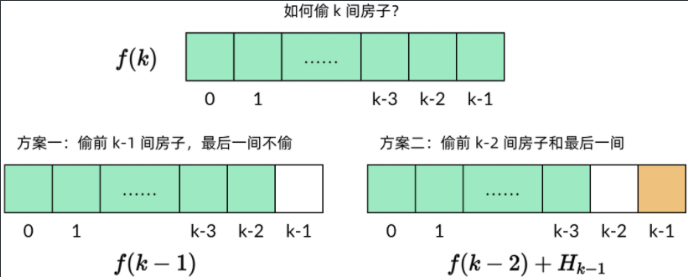
The last of the K houses is Hk − 1. If you don't steal the house, the problem becomes the largest amount stolen from the first k-1 house, that is, sub problem f(k-1). If you steal this house, the previous house Hk − 2 obviously cannot be stolen, and other houses will not be affected. Then the problem becomes the largest amount stolen in the first k-2 houses. In both cases, select the result with larger amount.
f(k)=max{f(k−1),Hk−1+f(k−2)}

When writing the recurrence relation, pay attention to the basic situation of k=0 and k=1:
When k=0, there is no house, so f(0)=0.
When k=1, there is only one house. You can steal the house, so f(1)=H0. In this way, a complete recursive relationship can be formed, and the code written later is not easy to make mistakes in boundary conditions.

For 3: dynamic programming has two calculation orders: one is the top-down recursive method using memo, and the other is the bottom-up cyclic method using dp array. However, in ordinary dynamic programming problems, 99% of the cases we do not need to use the memo method, so we'd better stick to the bottom-up dp array.
DP array can also be called "sub problem array", because each element in DP array corresponds to a sub problem. As shown in the figure below, dp[k] corresponds to sub problem f(k), that is, the maximum amount of stealing the first k houses.

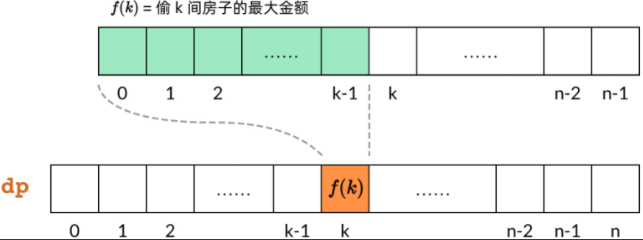
As long as the calculation order of the subproblem is clear, the calculation order of the DP array can be determined. For the thief problem, we analyze the dependencies of subproblems and find that each f(k) depends on f(k-1) and f(k-2). That is, dp[k] depends on dp[k-1] and dp[k-2], as shown in the figure below.

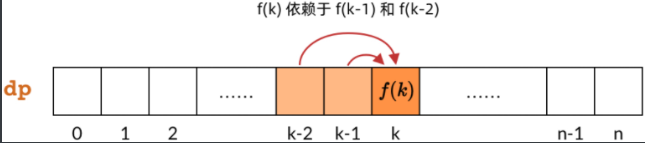
Since the dependencies in the DP array point to the right, the calculation order of the DP array is from left to right. In this way, we can ensure that when calculating a subproblem, the subproblems it depends on have been calculated

// Code up to step
public int rob(int[] nums) {
    if (nums.length == 0) {
        return 0;
    }
    // Sub question:
    // f(k) = steal the maximum amount in [0...k) room

    // f(0) = 0
    // f(1) = nums[0]
    // f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }

    int N = nums.length;
    int[] dp = new int[N+1];
    // No house, only for f(k) dependent on f(k-1) and f(k-2)
    dp[0] = 0;
    // Profit from stealing the first house
    dp[1] = nums[0];
    // Start with the second house
    for (int k = 2; k <= N; k++) {
        // Compare the two stealing methods, which is more profitable
        dp[k] = Math.max(dp[k-1], nums[k-1] + dp[k-2]);
    }
    return dp[N];
}

For 4: the basic principle of space optimization is that we don't always need to hold all DP arrays. For the thief problem, we find that only f(n-1) and f(n-2) are used in the last step of calculating f(n) In fact, the subproblems before n-3 have not been used for a long time. Then, we can save the results of the two subproblems with only two variables and calculate all subproblems in turn. The following dynamic graph compares the comparison relationship before and after spatial optimization:

// Final code
public int rob(int[] nums) {
    int prev = 0;
    int curr = 0;

    // For each cycle, calculate the "maximum amount to steal the current house"
    for (int i : nums) {
        // At the beginning of the cycle, curr represents dp[k-1], prev represents dp[k-2]
        // dp[k] = max{ dp[k-1], dp[k-2] + i }
        int temp = Math.max(curr, prev + i);
        prev = curr;
        curr = temp;
        // At the end of the loop, curr represents dp[k], prev represents dp[k-1]
    }

    return curr;
}