48. Medium difficulty:
Requirement: rotate the image in place
Method 1: clockwise circulation from outside to inside:
class Solution {
public void rotate(int[][] matrix) {
if(matrix.length == 0 || matrix.length != matrix[0].length) { //If the array passed is not equilateral or the element is 0, it is returned
return;
}
int nums = matrix.length; //Two dimensional array
int times = 0; //The outermost box is 0 and + 1 layer by layer inward. Start with 0 because the array subscript starts with 0
//Num > > 1 means num divided by 2 ^ 1, that is, how many layers of boxes are there from outside to inside. times represents the number of layers, < = it represents the maximum number of layers
while(times <= (nums >> 1)){ //Cycle through each layer of boxes. Use less than or equal to the reason to see the following explanation
int len = nums - (times << 1); //Times < < 1 means times*2^1. len is the side length of the current frame
//Swap the four edges of the current box. Each edge has len elements (0~len-1), so cycle len-1 times and exchange one element of each of the four edges each time
for(int i = 0; i < len - 1; ++i){
//If you can't imagine the exchange part below, please watch it in combination with the structure of the input array
int temp = matrix[times][times + i];
matrix[times][times + i] = matrix[times + len - i - 1][times];
matrix[times + len - i - 1][times] = matrix[times + len - 1][times + len - i - 1];
matrix[times + len - 1][times + len - i - 1] = matrix[times + i][times + len - 1];
matrix[times + i][times + len - 1] = temp;
}
++times; //After finishing the work of one layer box, start to operate the next layer box
}
}
}
There are no more than n/2 layers (a single central element is not counted as one layer) rectangular boxes from the outside to the inside.
(why n/2 layers: because the width of each lower layer is reduced by 2, the matrix of n*n has at most n/2 layers)
For the rectangular frame on the times layer, the frame side length len=nums − (times * 2),
(times starts from 0, the outermost layer is layer 0, and num is the length of the two-dimensional array)
Divide it clockwise into four len − 1 edges, and carry out cyclic exchange of elements on the four edges.
Key parts: exchange elements:
int temp = matrix[times][times + i]; matrix[times][times + i] = matrix[times + len - i - 1][times]; matrix[times + len - i - 1][times] = matrix[times + len - 1][times + len - i - 1]; matrix[times + len - 1][times + len - i - 1] = matrix[times + i][times + len - 1]; matrix[times + i][times + len - 1] = temp;
1. First line code:
Save the value of the first element with temp, then save the value of the second element in the address of the first element, the value of the third element in the address of the second element... Save the value of temp in the address of the last element.

2. Second line code:
The first element matrix[times] [times + i]: times represents the hierarchy of the current box (that is, the row position of the 2D array where the starting element to be processed is located, and the first element is taken from the first row of the current box) times+1 represents the position of the current element in the current edge (that is, the column in the current row of the current 2D array) The combination of the two means that the current element is in the position of the current two-dimensional array, and traverses each element at the edge of the current frame with the increment of i + 1.
The second element matrix[times + len - i - 1] [times]: times + len - i - 1 means that no matter where the row position of the previous element is, directly add the maximum number of rows (+ len). At this time, there may be overflow, so subtract the row position (- i) of the previous element. Because the subscript of the row position starts counting from 0, we added len instead of len-1, so - 1 (- 1). Since the second element is taken from the first column of the current box, the write times of the column position remains unchanged.

The third element matrix [times+len-1] [times + len - i - 1]: in times+len-1, because len changes dynamically and changes with the number of layers of the current box, times+len-1 will never overflow. Times is the number of rows of the first element. Just add the maximum len-1, which is the number of rows of the third element (that is, the symmetrical row relative to the row of the first element). times + len - i - 1: look directly at the following figure:

The fourth element matrix [times + i] [times + len-1]: times + i is incremented by i +1 because the number of rows is from top to bottom. Times + len-1 is because the column is symmetrical with the column of the second element, so the direct maximum value is len-1.

The full picture is as follows:
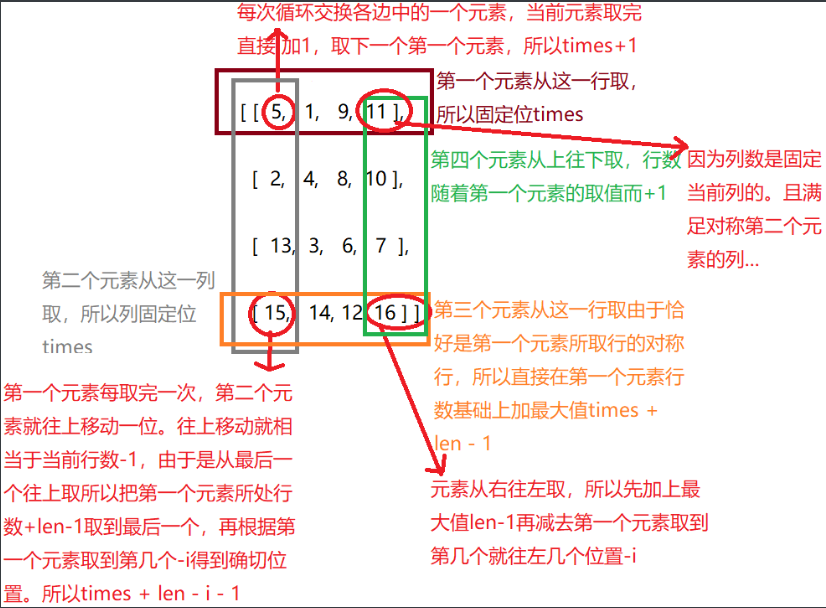
We found a coincidence:
① . the column value times + i of the first element is the same as the row value times + i of the fourth element,
② . the column value times of the second element is the same as the row value times of the first element,
③ . the column value times + len - i - 1 of the third element is the same as the row value of the second element,
④ . the column value times + len - 1 of the fourth element is the same as the row value of the third element.
For ① and ①, both are incremented by + 1 from the basic value, so times+i. According to the figure, the basic values are times (the first element is the same row + 1, and the fourth element is the same column + 1)
The values of ② and ② are unchanged, and the basic value is unchanged. The first element is the first row unchanged, and the second element is the first column unchanged.
The values of ③ and ③ are from the last bit forward to the basic value.
The values of ④ and ④ are the last bit unchanged.
Why is < = (Num > > 1)) used in while (times < = (Num > > 1)
int nums = matrix.length; Result: if the array matrix is [6] [10], then num is 6
times starts at 0
Nums > > 1 results in 3
In this way, the number of frames has 3 layers, but we have handled a total of 4 layers from 0 to 3.
However, whether we use < = or < in leetcode, the resu lt is correct and the time consumption is the same. This is outrageous.
Method 2: double flip:
class Solution {
public void rotate(int[][] matrix){
if(matrix.length == 0 || matrix.length != matrix[0].length) {
return;
}
int nums = matrix.length;
for (int i = 0; i < nums; ++i){
for (int j = 0; j < nums - i; ++j){
int temp = matrix[i][j];
matrix[i][j] = matrix[nums - 1 - j][nums - 1 - i];
matrix[nums - 1 - j][nums - 1 - i] = temp;
}
}
for (int i = 0; i < (nums >> 1); ++i){ //Horizontal centerline up and down
for (int j = 0; j < nums; ++j){
int temp = matrix[i][j];
matrix[i][j] = matrix[nums - 1 - i][j];
matrix[nums - 1 - i][j] = temp;
}
}
}
}
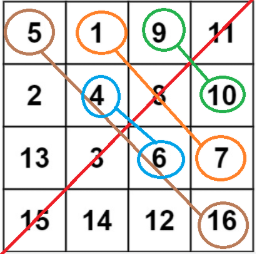
Principle: first flip along the diagonal line from top left to bottom right, and then flip up and down along the horizontal center line to achieve the rotation effect of 90 degrees clockwise. You can take a piece of paper and test it yourself.
The first for loop in the code can be represented by the following figure: Principle: the current element has nothing to do with its symmetrical element about the main diagonal: the row of the current element has nothing to do with the row of the symmetrical element, but the column of the current element is related to the row of the symmetrical element. As can be seen from the following figure, the row is the maximum number of rows (num-1) minus the number of columns (j) of the current element.
As long as we replace the upper triangular region, we will replace the whole region, so when we deal with row 0, we need to deal with all columns nums - i = nums - 0 = nums. As the number of rows increases, the number of columns we need to process decreases, so num - I.
344. Simple difficulty:
Method 1: double pointer: time complexity: O(N), space complexity: O(1)
class Solution {
public void reverseString(char[] s) {
int n = s.length;
for (int left = 0, right = n - 1; left < right; ++left, --right) {
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
}
}
}