Preface description
Algorithm learning, daily problem brushing records.
Topic connection
Topic content
Give you an array of rectangles, where rectangles[i] = [xi, yi, ai, bi] represents a rectangle with parallel coordinate axes. The lower left vertex of the rectangle is (xi, yi) and the upper right vertex is (ai, bi).
Returns true if all rectangles together exactly cover a rectangular area; Otherwise, false is returned.
Example 1:
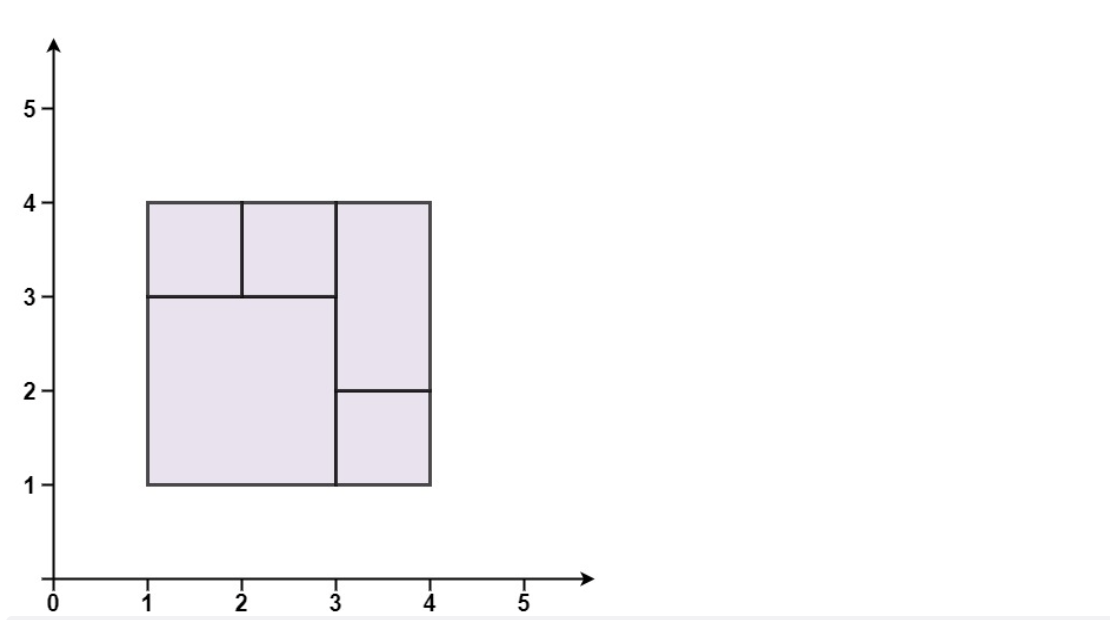
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: five rectangles together can accurately cover a rectangular area.
Example 2:
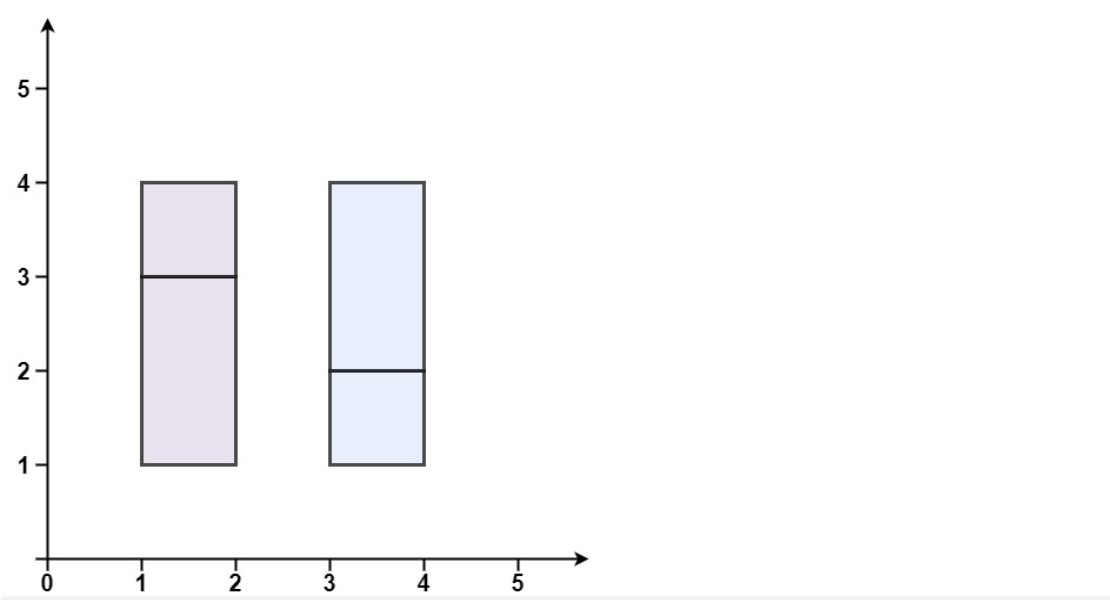
Input: rectangles = [[1,1,2,3], [1,3,2,4], [3,1,4,2], [3,2,4]]
Output: false
Explanation: there is a gap between two rectangles, which cannot be covered into a rectangle.
Example 3:
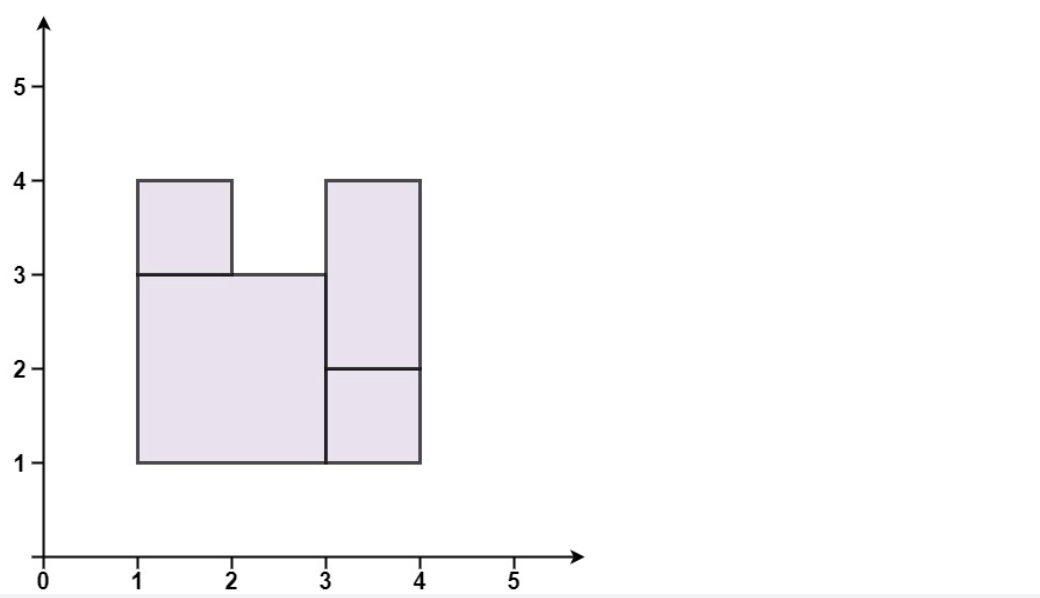
Input: rectangles = [[1,1,3,3], [3,1,4,2], [1,3,2,4], [3,2,4]]
Output: false
Explanation: there is a gap at the top of the figure, which cannot be covered into a rectangle.
Example 4:
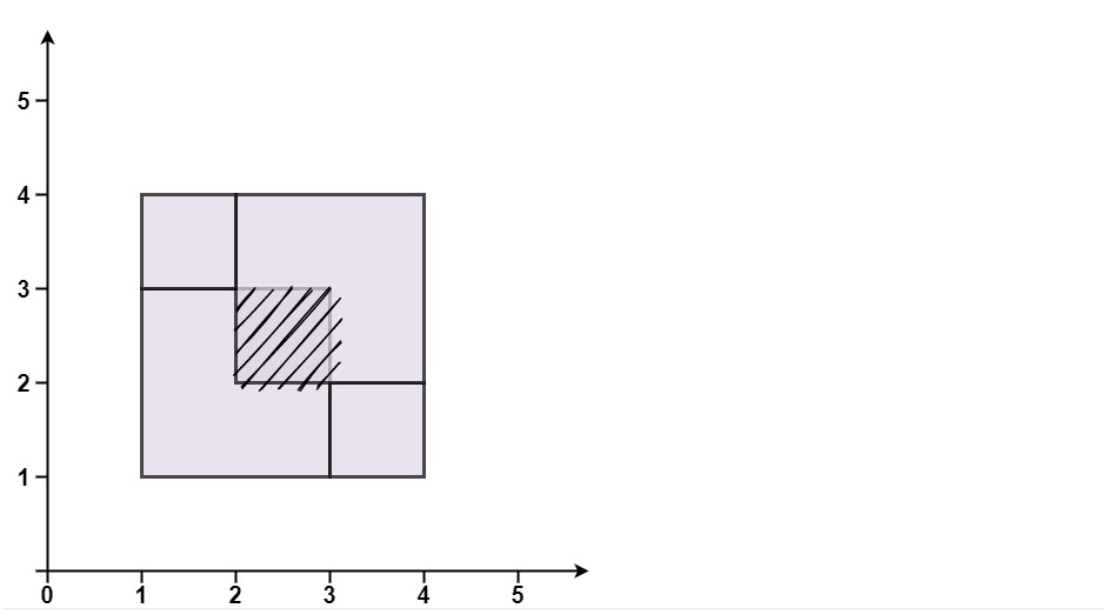
Input: rectangles = [[1,1,3,3], [3,1,4,2], [1,3,2,4], [2,2,4]]
Output: false
Explanation: because there is an intersection area in the middle, although it forms a rectangle, it is not accurately covered.
Tips:
1 <= rectangles.length <= 2 * 10^4
rectangles[i].length == 4
-10^5 <= xi, yi, ai, bi <= 10^5
Analysis process
Idea: to calculate whether the total area is equal, the four most vertices only appear once, and the other points only appear twice or four times, that is, the following two conditions are met.
Condition 1: calculate the sum of small rectangular areas, calculate the large rectangular area, and judge whether the sum of small rectangular areas is equal to the large rectangular area.
Condition 2: the four points at the bottom left, top left, bottom right and top right appear only once, and the other points appear in pairs, that is, they appear only 2 or 4 times.
analysis:
From the above four examples, it is easy to see that the sum of small rectangular areas must first be equal to the large rectangular area.
How to understand that the four points at the bottom left, top left, bottom right and top right only appear once? As a counterexample, the sum of the small rectangular area is equal to the large rectangular area, but the four points at the bottom left, the top left, the bottom right and the top right do not appear only once. Note that it only appears once, and it is impossible to appear zero or more times, as shown in the figure:
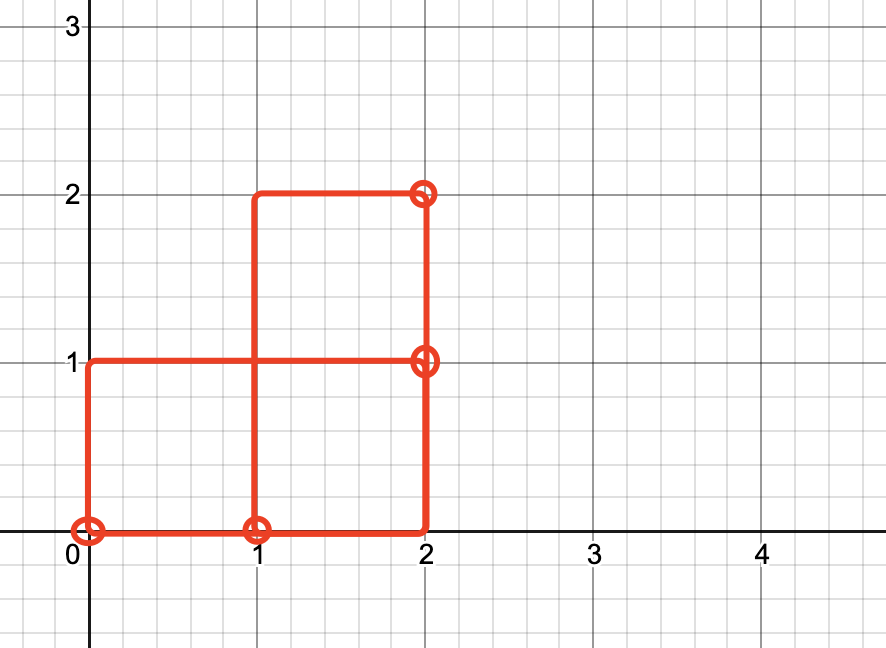
Input: rectangles = [[0,0,2,1],[1,0,2,2]]
The large rectangular area is 2 * 2 = 4, and the sum of the small rectangular areas is 2 * 1 + 1 * 2 = 4. The sum of the small rectangular areas is equal to the large rectangular area, but it is not a perfect rectangle because it does not accurately cover a rectangular area, where there are overlaps and intersections. The four points at the bottom left, top left, bottom right and top right do not appear only once, and the top left vertex (0,2) Zero occurrences.
How to understand that other points appear in pairs, that is, only twice or four times? Similarly, a counterexample can be given. The sum of the small rectangular area is equal to the large rectangular area. At the same time, the four points at the bottom left, top left, bottom right and top right only appear once, but other points do not appear in pairs, as shown in the figure:
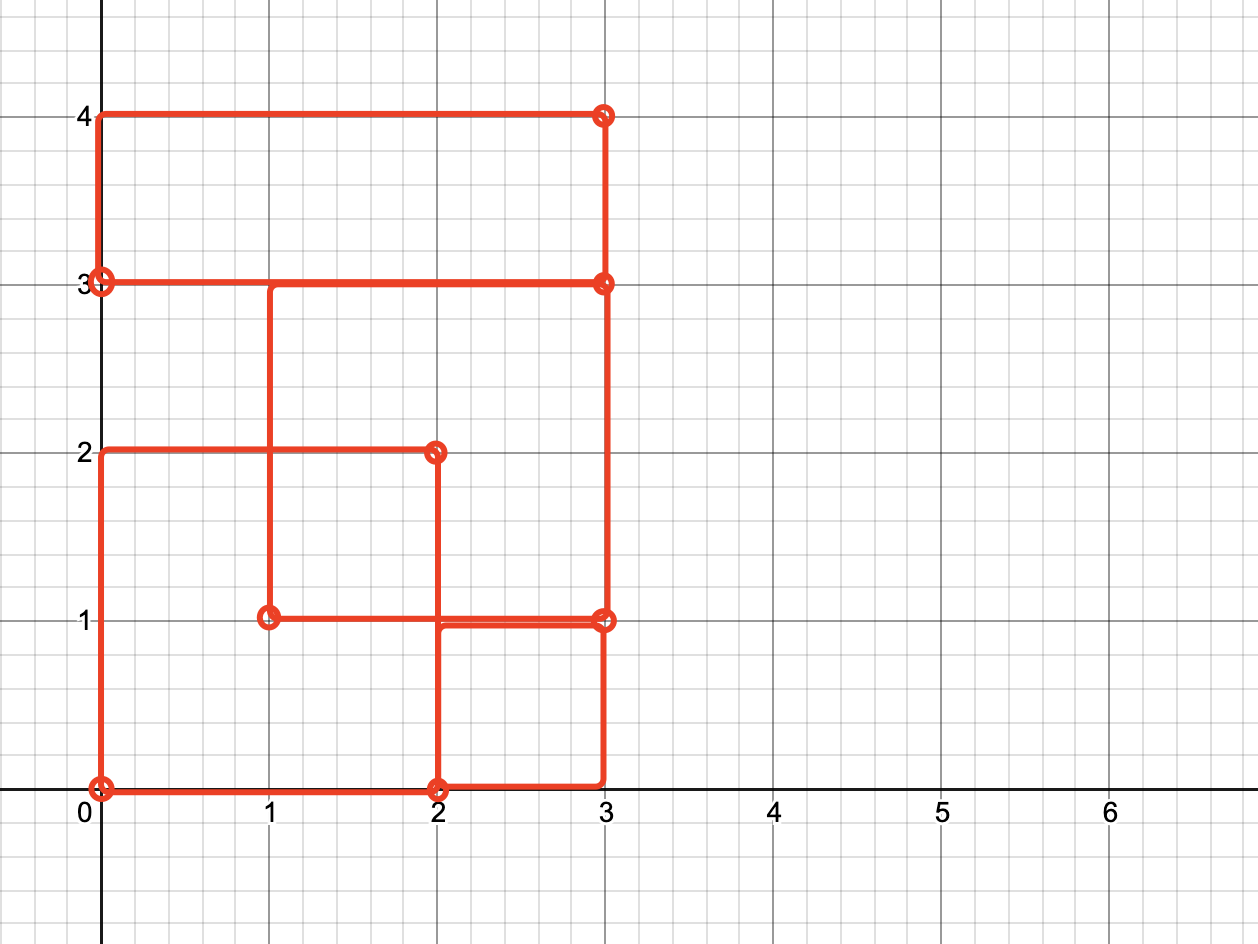
Input: rectangles = [[0,0,2,2],[1,1,3,3],[2,0,3,1],[0,3,3,4]]
The large rectangular area is 3 * 4 = 12, and the sum of the small rectangular areas is 2 * 2 + 2 * 2 + 1 * 1 + 3 * 1 = 12. The sum of the small rectangular areas is equal to the large rectangular area. The four points at the bottom left, top left, bottom right and top right only appear once, respectively (0,0), (0,4), (3,0), (3,4), but they are not perfect rectangles because they do not accurately cover a rectangular area, There are overlapping places, but other points here do not appear in pairs. For example: (0,2) only appears once.
It can be imagined that if a rectangular area is accurately covered, there are no intersecting areas, but only the immediately adjacent points, as shown in the figure:
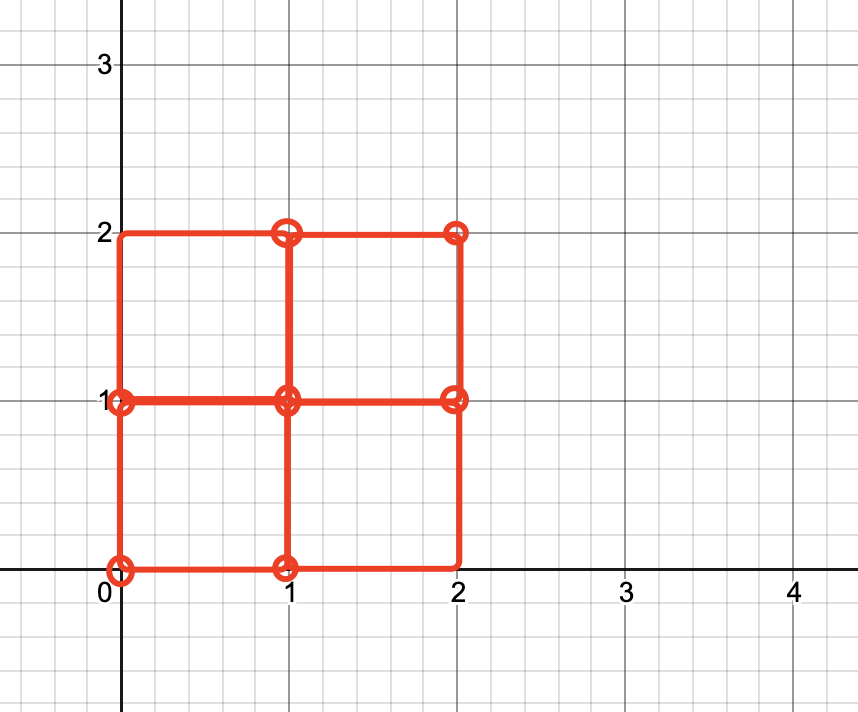
If two rectangular areas are adjacent, the common point just belongs to two rectangles and appears twice; If four rectangular areas are adjacent, the common point just belongs to four rectangles and appears four times; Because it accurately covers the rectangular area, it will not be three rectangular areas, so it can be seen from here that other points only appear twice or four times.
First step
Define the sum of small rectangular areas, which is initially 0.
Define the bottom left abscissa minX, initially the first vertex of the first rectangle.
Define the bottom left ordinate minY, which is initially the second vertex of the first rectangle.
Defines the top right abscissa maxX, initially the third vertex of the first rectangle.
Define the rightmost vertical coordinate maxY, which is initially the fourth vertex of the first rectangle.
Step 2
Traverse the input list of small rectangles and calculate the sum of small rectangular areas.
During each traversal:
Small rectangle length = ai - xi.
Small rectangle width = bi - yi.
sum of small rectangle areas is calculated by accumulation. sum of small rectangle areas = length of small rectangle * width of small rectangle.
xi is compared with the bottom left abscissa minX, yi is compared with the bottom left ordinate minY, and the bottom left abscissa minX and bottom left ordinate minY are updated, that is, the bottom left vertex is updated.
ai is compared with the top right abscissa maxX, bi is compared with the top right ordinate maxY, and the bottom left abscissa minX and bottom left ordinate minY are updated, that is, the top right vertex is updated.
After traversal, calculate the large rectangular area area.
Large rectangle area = large rectangle length * large rectangle width = (top right abscissa - bottom left abscissa) * (top right ordinate - bottom left ordinate) = (maxX - minX) * (maxY - minY).
Step 3
If sum of the small rectangular area is equal to the large rectangular area area, judge whether the four points at the bottom left, top left, bottom right and top right only appear once, and judge whether other points appear in pairs, that is, only twice or four times. Otherwise, if the perfect rectangular condition is not met, return false directly.
Step 4
When judging whether the four points at the bottom left, top left, bottom right and top right only appear once, and whether other points appear in pairs:
Define the leftBottomCount of the leftmost and lower coordinates, initially 0.
Define the number of leftTopCount coordinates at the top left, initially 0.
Define the rightBottomCount of the lowest right coordinate, which is initially 0.
Defines the rightTopCount of the rightmost top coordinates, which is initially 0.
Define a set map to store the number of non vertex coordinates.
Traverse the input small rectangular list rectangles again. Each time:
Since the top, bottom, left and right four vertices have been found above, you can judge whether the four vertices of each small rectangle are the top vertices.
If it is the most vertex, add 1 to the number of the most vertex coordinates in the corresponding direction. If the number of the most vertices occurs more than once, it directly returns false.
If it is not the most vertex, it is not the most vertex. Use the set map to record their number, and the key value of the map is expressed in the form of abscissa ordinate.
After traversing the input small rectangular list rectangles, traverse the set map to determine whether the number of non vertex coordinates appears in pairs, that is, whether the number is 2 or 4.
Step 5
Each time you traverse the set map:
If the number of non vertex coordinates is not equal to 2 or 4, return false directly.
After traversing the set map, judge whether the four points at the bottom left, top left, bottom right and top right only appear once. If they all appear only once, return true, otherwise return false.
Answer code
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
// Condition 1: calculate the sum of the small rectangular area, calculate the large rectangular area, and judge whether the sum of the small rectangular area is equal to the large rectangular area
// Condition 2: the four points at the bottom left, top left, bottom right and top right only appear once, and the other points appear in pairs, that is, only twice or four times
// Sum of small rectangular areas
int sum = 0;
// Bottom left abscissa
int minX = rectangles[0][0];
// Bottom left ordinate
int minY = rectangles[0][1];
// Top right abscissa
int maxX = rectangles[0][2];
// Top right ordinate
int maxY = rectangles[0][3];
// Traverse small rectangle
for (int[] rectangle : rectangles) {
// Small rectangle length
int length = rectangle[2] - rectangle[0];
// Small rectangle width
int width = rectangle[3] - rectangle[1];
// Calculate the sum of small rectangular areas by accumulation
sum += length * width;
if (rectangle[0] <= minX && rectangle[1] <= minY) {
// Update bottom left abscissa
minX = rectangle[0];
// Update bottom left ordinate
minY = rectangle[1];
}
if (rectangle[2] >= maxX && rectangle[3] >= maxY) {
// Update top right abscissa
maxX = rectangle[2];
// Update top right ordinate
maxY = rectangle[3];
}
}
// Calculate large rectangular area
int area = (maxX - minX) * (maxY - minY);
if (sum == area) {
// If the sum of the small rectangular area is equal to the large rectangular area, judge whether the four points at the bottom left, top left, bottom right and top right only appear once
// Number of bottom left coordinates
int leftBottomCount = 0;
// Number of top left coordinates
int leftTopCount = 0;
// Number of bottom right coordinates
int rightBottomCount = 0;
// Number of top right coordinates
int rightTopCount = 0;
// Defines a collection that holds the number of non vertex coordinates
Map<String, Integer> map = new HashMap<>();
// Traverse the small rectangle again
for (int[] rectangle : rectangles) {
if (rectangle[0] == minX && rectangle[1] == minY) {
// The number of bottom left coordinates plus 1
++leftBottomCount;
if (leftBottomCount > 1) {
// If the number of bottom left coordinates is greater than 1, false is returned directly
return false;
}
} else {
// If it is not the lowest left coordinate, update the number of non vertex coordinates in the set
String lb = rectangle[0] + "-" + rectangle[1];
map.put(lb, map.getOrDefault(lb, 0) + 1);
}
if (rectangle[0] == minX && rectangle[3] == maxY) {
// Number of top left coordinates plus 1
++leftTopCount;
if (leftTopCount > 1) {
// If the number of top left coordinates is greater than 1, return false directly
return false;
}
} else {
// If it is not the top left coordinate, update the number of non vertex coordinates in the set
String lt = rectangle[0] + "-" + rectangle[3];
map.put(lt, map.getOrDefault(lt, 0) + 1);
}
if (rectangle[2] == maxX && rectangle[1] == minY) {
// The number of bottom right coordinates plus 1
++rightBottomCount;
if (rightBottomCount > 1) {
// If the number of bottom right coordinates is greater than 1, false is returned directly
return false;
}
} else {
// If it is not the bottom right coordinate, update the number of non vertex coordinates in the set
String rb = rectangle[2] + "-" + rectangle[1];
map.put(rb, map.getOrDefault(rb, 0) + 1);
}
if (rectangle[2] == maxX && rectangle[3] == maxY) {
// Number of top right coordinates plus 1
++rightTopCount;
if (rightTopCount > 1) {
// If the number of top right coordinates is greater than 1, return false directly
return false;
}
} else {
// If it is not the top right coordinate, update the number of non vertex coordinates in the set
String rt = rectangle[2] + "-" + rectangle[3];
map.put(rt, map.getOrDefault(rt, 0) + 1);
}
}
// Traverse the set to determine whether the number of non vertex coordinates are in pairs, that is, whether the number is 2 or 4
for (Map.Entry<String, Integer> entry : map.entrySet()) {
if (entry.getValue() != 2 && entry.getValue() != 4) {
// If the number of non vertex coordinates is not equal to 2 or 4, false is returned
return false;
}
}
// If the bottom left, top left, bottom right and top right points only appear once, return true
return leftBottomCount == 1 && leftTopCount == 1 && rightBottomCount == 1 && rightTopCount == 1;
}
// If the sum of the small rectangular area is not equal to the large rectangular area, return false directly
return false;
}
}
Submit results
The execution time was 46ms, the time beat 57.21% of users, the memory consumption was 47.6MB, and the space beat 18.97% of users.
Original link
Original link: Perfect rectangle