The closest sum of three

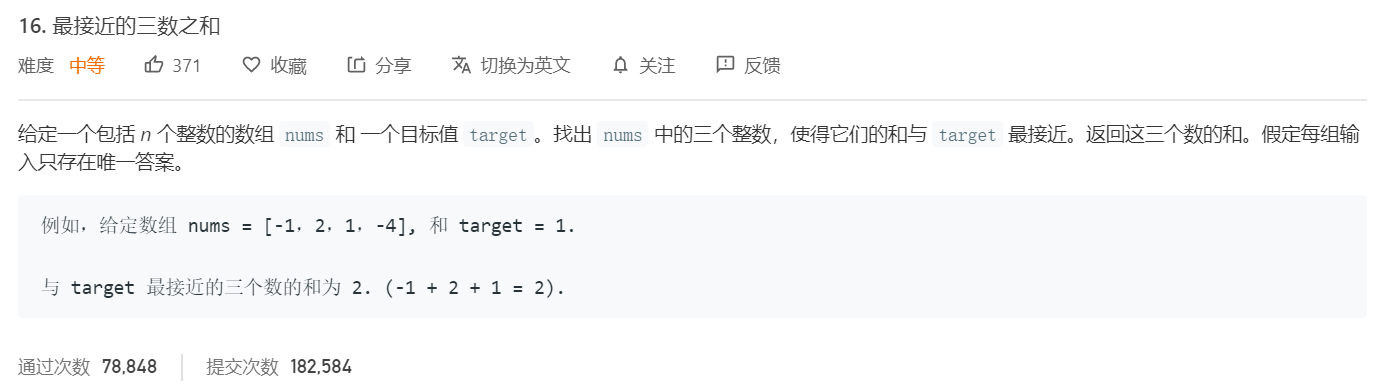
Title Description:

Solutions:

• First, this problem is similar to the sum of the three numbers of the previous one, so this solution is also a sort+ In general, the writing method of double pointer is the same as the sum of three numbers. It also needs to be de duplicated and simplified. Then, it needs to find the difference between the final sum of three numbers and the target given by the topic. If the difference is equal to zero, return this sum directly. If it is greater than zero or less than zero, continue to narrow the range to see if it can make the difference diff closer to 0, and finally return it closer to 0 The number.

class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        lens = len(nums)
        nums.sort()
        # Let the minimum difference be infinite
        mini = float('inf')
        closesum = 0
        if lens == 3:
            return sum(nums)
        else:
            for i in range(lens-2):
                if i > 1 and nums[i] == nums[i-1]:
                    continue
                L = i + 1
                R = lens - 1
                while L < R:
                    Sum = nums[i] + nums[L] + nums[R]
                    diff = Sum - target
                    if abs(diff) < mini:
                        mini = abs(diff)
                        closesum = Sum
                    if diff == 0:
                        return Sum
                    elif diff > 0:
                        R -= 1
                        while L<R and nums[R] == nums[R+1]:
                            R -= 1
                    else:
                        L += 1
                        while L<R and nums[L] == nums[L-1]:
                            L += 1
        return closesum

• Second, this method is similar to the sum of the last three numbers. It uses the dichotomy to get an initial value, and then it is also the method of double pointer. Compared with target, I find that there is a special wonder that the increase or decrease of the last double pointer here does not need to use if and else. You can return 1 if you hold the characteristics of the comparison operator and return 1 if you hold it Back to 0, a lot of code has been reduced, which is worth learning.

class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        nums.sort()
        res = float('inf')
        lens = len(nums)
        for i in range(lens - 2):
            L = max(i + 1,bisect.bisect_left(nums, target - nums[lens-1] - nums[i], i+1, lens-1)-1)
            R = lens-1
            while L < R and res != target:
                Sum = nums[i] + nums[L] + nums[R]
                res = min(res, Sum, key=lambda x: abs(x - target))
                L = L + (Sum < target)
                R = R - (Sum > target)
        return res

• Third: Based on the first method, we have made some improvements. Here, we divide the whole into three parts. First, we use mini and maxi to get the sum of the minimum and the maximum three numbers, and then compare them with target. If the minimum sum is greater than target or the maximum sum is less than target, then the sum is the closest sum of the three numbers, and the answer will come out. After removing the sum of the maximum and the minimum, and then discussing the sum of these three numbers in the middle, the solution here is no different from the first method. It needs to be de duplicated as well. When the absolute value is smaller, it will be assigned back to res, and finally it will return the minimum absolute value res.

class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        nums.sort()
        res = float('inf')
        lens = len(nums)
        for i in range(lens-2):
            if i > 0 and nums[i] == nums[i-1]: 
                continue
            L = i + 1
            R = lens - 1
            mini = nums[i] + nums[L] + nums[L+1]
            maxi = nums[i] + nums[R-1] + nums[R]
            if mini > target:
                if abs(mini - target) < abs(res - target):
                    res = mini
                break
            if maxi < target:
                if abs(maxi - target) < abs(res - target):
                    res = maxi
                continue   
            while L < R:
                Sum = nums[i] + nums[L] + nums[R]
                if Sum == target:
                    return target
                if abs(Sum - target) < abs(res - target):
                    res = Sum
                if Sum < target:
                    L += 1
                    while L < R and nums[L] == nums[L-1]: 
                        L += 1
                if Sum > target:
                    R -= 1
                    while L < R and nums[R] == nums[R+1]: 
                        R -= 1
        return res