subject

There is an undirected graph with n nodes. Each of these nodes has a unique number between 0 and n - 1. Give you a two-dimensional array graph, where graph[u] is an array of nodes, which is composed of adjacent nodes of node U. Formally, for each V in graph[u], there is an undirected edge between node u and node v. The undirected graph also has the following properties:

• There is no self ring (graph[u] does not contain U).
• There are no parallel edges (the graph[u] does not contain duplicate values).
• If V is in graph[u], then u should also be in graph[v] (the graph is undirected)
• This graph may not be a connected graph, that is, there may not be a path connecting two nodes u and v.

Definition of bipartite graph: if the node set of a graph can be divided into two independent subsets A and B, and the two nodes of each edge in the graph come from set a and set B, the graph is called bipartite graph.

If the graph is bipartite, return true; otherwise, return false.

Example 1:

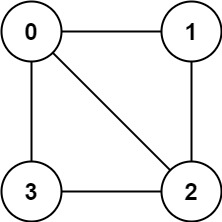
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
 Explanation: nodes cannot be divided into two independent subsets so that each edge connects a node in one subset with a node in another subset.

Example 2:

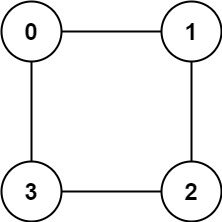
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
 Explanation: nodes can be divided into two groups: {0, 2} and {1, 3} . 

Tips:

• g r a p h . l e n g t h = = n graph.length == n graph.length==n
• 1 < = n < = 100 1 <= n <= 100 1<=n<=100
• 0 < = g r a p h [ u ] . l e n g t h < n 0 <= graph[u].length < n 0<=graph[u].length<n
• 0 < = g r a p h [ u ] [ i ] < = n − 1 0 <= graph[u][i] <= n - 1 0<=graph[u][i]<=n−1
• g r a p h [ u ] graph[u] graph[u] will not contain u u u
• g r a p h [ u ] graph[u] All values of graph[u] are different from each other
• If g r a p h [ u ] graph[u] graph[u] contains v v v. So g r a p h [ v ] graph[v] The graph[v] also contains u u u

Problem solution

[preface]

For any two nodes in the graph u u u and v v v. If there is an edge directly connected between them, then u u u and v v v must belong to a different set.

If a given undirected graph is connected, we can start with any node and dye it red. Then we traverse the whole graph and dye all the nodes directly connected to this node green, indicating that these nodes cannot belong to the same set as the starting node. Then we dye all the nodes directly connected to these green nodes red, and so on Every node in an undirected graph is colored.

If we can dye successfully, the red and green nodes belong to a set, and the undirected graph is a bipartite graph; if we fail to dye successfully, that is, in the process of dyeing, we access a dyed node at a certain time, and its color is different from the color we are going to dye, it means that the undirected graph is not a bipartite graph Plot.

[algorithm flow]

We choose any node to start, dye it red, and traverse the whole undirected graph from this node;

In the process of traversal, if we pass through the node u u u traversed the node v v v (i.e u u u and v v v) if there is an edge directly connected in the figure, there will be two cases:

• If v v v is not dyed, then we dye it with u u u different colors and pairs v v v traverse directly connected nodes;
• If v v v is dyed and the color is the same as u u If u is the same, then the given undirected graph is not a bipartite graph. We can directly exit the traversal and return False \text{False} False as the answer.
• When the traversal ends, it indicates that the given undirected graph is a bipartite graph, and returns True \text{True} True as the answer.

We can use "depth first search" or "breadth first search" to traverse the undirected graph. The corresponding codes of these two searches are given below.

Note: the undirected graph given in the question does not necessarily guarantee connectivity, so we need to traverse multiple times until each node is dyed or the answer is False \text{False} False. At the beginning of each traversal, we select any node that is not dyed and dye all nodes directly or indirectly connected to the node.

Solution 1: depth first search

class Solution {
private:
    static constexpr int UNCOLORED = 0;
    static constexpr int RED = 1;
    static constexpr int GREEN = 2;
    vector<int> color;
    bool valid;
public:
    void dfs(int node, int c, const vector<vector<int>> &graph) {
        color[node] = c;
        int cNei = (c == RED ? GREEN : RED);
        for (int neighbor : graph[node]) {
            if (color[neighbor] == UNCOLORED) {
                dfs(neighbor, cNei, graph);
                if (!valid) return ;
            } else if (color[neighbor] != cNei) {
                valid = false;
                return ;
            }
        }
    }
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        valid = true;
        color.assign(n, UNCOLORED);
        for (int i = 0; i < n && valid; i++) {
            if (color[i] == UNCOLORED) {
                dfs(i, RED, graph);
            }
        }
        return valid;
    }
};

[complexity analysis]

• Time complexity: O ( N + M ) O(N+M) O(N+M), where N N N and M M M is the number of points and edges in an undirected graph, respectively.
• Space complexity: O ( N ) O(N) O(N), the array of storage node colors needs O ( N ) O(N) O(N), and in the process of depth first search, the maximum depth of the stack is N N N. Need O ( N ) O(N) O(N).

Solution 2: breadth first search

class Solution {
private:
    static constexpr int UNCOLORED = 0;
    static constexpr int RED = 1;
    static constexpr int GREEN = 2;
    vector<int> color;    
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        color.assign(n, UNCOLORED);
        for (int i = 0; i < n; i++) {
            if (color[i] == UNCOLORED) {
                queue<int> que;
                que.push(i);
                color[i] = RED;
                while (!que.empty()) {
                    int node = que.front();
                    int cNei = (color[node] == RED ? GREEN : RED);
                    que.pop();
                    for (int neighbor : graph[node]) {
                        if (color[neighbor] == UNCOLORED) {
                            que.push(neighbor);
                            color[neighbor] = cNei;
                        } else if (color[neighbor] != cNei) {
                            return false;
                        }
                    }
                }
            }
        }
        return true;
    }
};

[complexity analysis]

• Time complexity: O ( N + M ) O(N+M) O(N+M), where N N N and M M M is the number of points and edges in an undirected graph, respectively.
• Space complexity: O ( N ) O(N) O(N), the array of storage node colors needs O ( N ) O(N) O(N), and in the process of breadth first search, there are at most in the queue N − 1 N−1 N − 1 node, required O ( N ) O(N) O(N).

Solution 3: joint search set

[ideas]

According to the definition of a bipartite graph, two points on an edge should be in different sets. Therefore, traverse each point in the graph and merge all adjacent points of the point. If any of the adjacent points is in the same set as the current point, the graph is not a bipartite graph.

[Code]

class UnionSet {
private:
    vector<int> parent;
    vector<int> rank;
public:
    UnionSet(int n) {
        parent.resize(n);
        rank.resize(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    int find(int u) {
        return parent[u] == u ? u : parent[u] = find(parent[u]);
    }

    bool isConnected(int u, int v) {
        return find(u) == find(v);
    }

    void merge(int u, int v) {
        int pu = find(u), pv = find(v);
        if (pu == pv) return ;
        if (rank[pu] < rank[pv]) {
            parent[pu] = pv;
            rank[pv] += rank[pu];
        } else {
            parent[pv] = pu;
            rank[pu] += rank[pv];
        }
    }
};

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        UnionSet us(graph.size());
        for (int i = 0; i < graph.size(); i++) {
            for (int j = 0; j < graph[i].size(); j++) {
                //Judge whether the point adjacent to point i is in the same set as point i
                //If it is in the same set, it directly returns false
                if (us.isConnected(graph[i][j], i)) return false;
                //If it is not in the same set, the adjacent points will be merged. Note: it is the adjacent point that is merged, not the point and the adjacent point
                us.merge(graph[i][0], graph[i][j]);
            }
        }
        return true;
    }
};

[complexity analysis]

• Time complexity: O ( m + n ) O(m + n) O(m+n), where m m m and n n n is the number of points and edges of an undirected graph, respectively.
• Space complexity: O ( m ) O(m) O(m), where m m m is the number of points of an undirected graph.