Original title:

Given an integer n, find the closest integer (not including itself), which is a palindrome.
The 'closest' is defined as absolute difference minimized between two integers.

Example 1:
Input: "123"
Output: "121"

Note:
The input n is a positive integer represented by string, whose length will not exceed 18.
If there is a tie, return the smaller one as answer.

Train of thought:
The main idea of the title is to give a number (in the form of a string) and output the palindrome number nearest to the number (in the form of a string). For example, input "123" and output "121" if the nearest palindrome number is 121. If you want to be close, you should try to be as high as possible. Careful analysis shows that there are only three possibilities for palindrome numbers closest to a number. Take "123456789" as an example. First, palindromes should be symmetrical left and right. The left side of "123456789" is "12345", and the corresponding palindrome number is "123454321" (midnum in the code). Of course, "123454321" is not necessarily the closest, but it may also be "123444321" (minnum in code) or "123464321" (maxnum in code), with "12344" ("12345-1") and "12346" ("12345+1") on the left. In addition, we should also consider the number of digits in the left half of the number "+1" or "-1". For example, 9999, 99 on the left, 99 + 1 = 100, the nearest number can not take into account "100001", but should be "10001", so the number of digits on the left side "+1" or "-1" should be given special consideration. The time complexity of the algorithm is O(1).

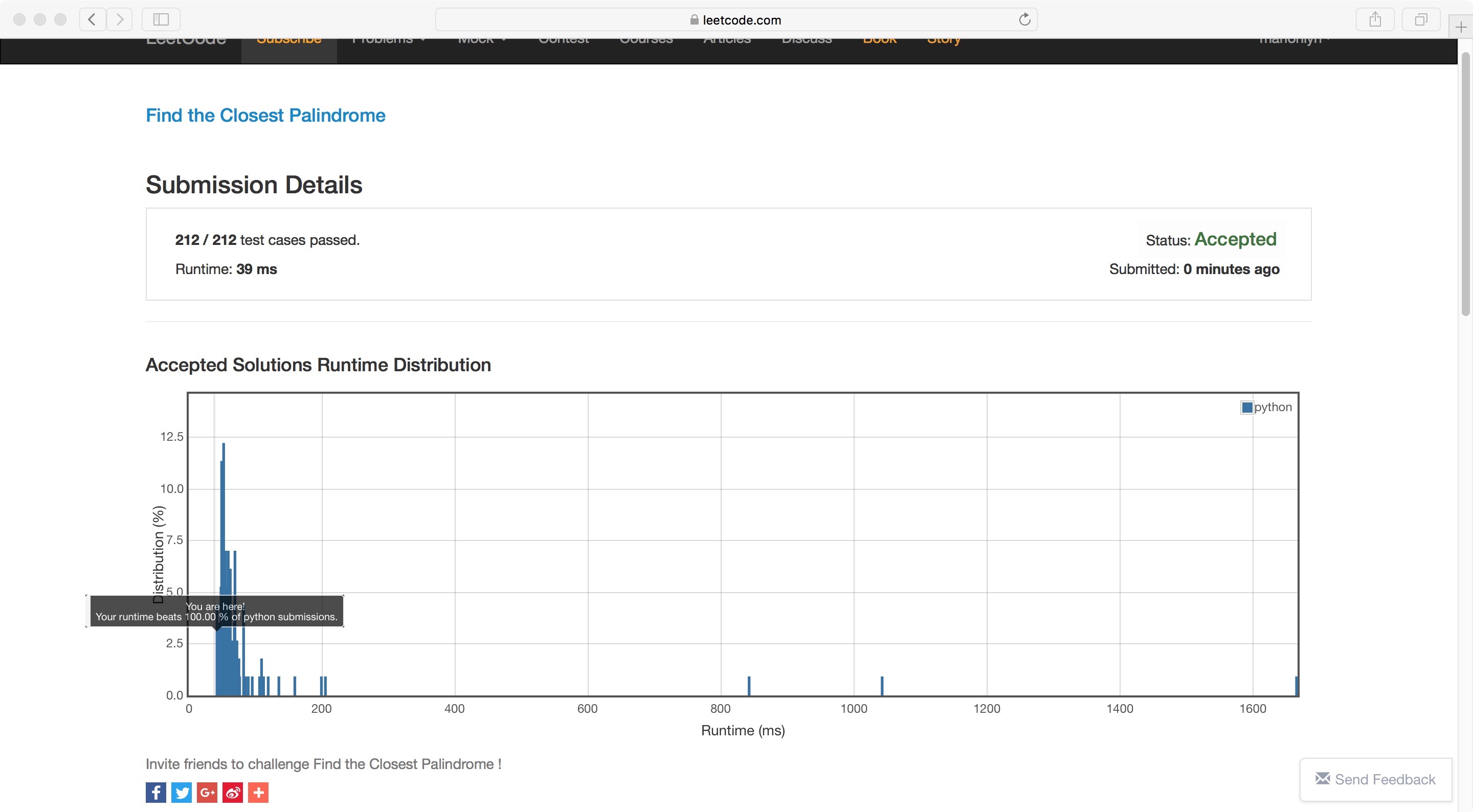
Code: (39ms passed, even defeated 100%python code!)

class Solution(object):

    # Judge whether + 1 or - 1 changes in digits
    def change_bit(self, n):
        if(len(str(n+1))!=len(str(n))):
            return 1
        elif((len(str(n-1))!=len(str(n)))or(n==1)):
            return -1
        else:
            return 0

    # Find out the nearest number to n in minnum, midnum and maxnum. If the distance is the same, find the smallest number.
    def find_min(self,minnum,midnum,maxnum,n):
        minabs=abs(long(minnum)-long(n))
        midabs=abs(long(midnum)-long(n))
        maxabs=abs(long(maxnum)-long(n))
        if(midabs<=maxabs):
            if(minabs<=midabs):
                return minnum
            else:
                return midnum
        else:
            if(minabs<=maxabs):
                return minnum
            else:
                return maxnum

    def nearestPalindromic(self, n):
        # Only one digit
        if(len(n)<2):
            return str(int(n)-1)
        # The case of even digits
        if((len(n)%2)==0):
            substr_front=n[0:len(n)//2]
            midnum=substr_front+substr_front[::-1]
            maxsub_front=str(int(substr_front)+1)
            maxnum=maxsub_front+maxsub_front[::-1]
            minsub_front=str(int(substr_front)-1)
            minnum=minsub_front+minsub_front[::-1]
        # The case of odd digits
        else:
            substr_front=n[0:(len(n)+1)//2]
            midnum=substr_front+(substr_front[::-1])[1:len(substr_front)]
            maxsub_front=str(int(substr_front)+1)
            maxnum=maxsub_front+(maxsub_front[::-1])[1:len(maxsub_front)]
            minsub_front=str(int(substr_front)-1)
            minnum=minsub_front+minsub_front[::-1][1:len(minsub_front)]
        # It is the case of palindrome itself, midabs=0, does not meet the requirements, so the midnum is initialized to "0" to achieve the goal that midabs must be greater than max(maxabs,minabs)
        if(midnum==n):
            midnum="0"
        # The number of digits in plus 1
        if(self.change_bit(int(substr_front))==1):
            maxnum=""
            maxnum='1'+((len(n)-1)*'0')+'1'
        # If the number of digits changes after subtraction 1, be careful to include 1-1=0.
        if(self.change_bit(int(substr_front))==-1):
            minnum=""
            minnum=(len(n)-1)*'9'
        # print(minnum)
        # print(midnum)
        # print(maxnum)
        return self.find_min(minnum,midnum,maxnum,n)

# IndentationError: unindent does not match any outer indentation level
# The indentation problem caused by the mixed use of space and tab keys
# testing
# s=Solution()
# print(s.nearestPalindromic("1234"))