Jump game, three questions in total.

55. Jump Game

1. topic

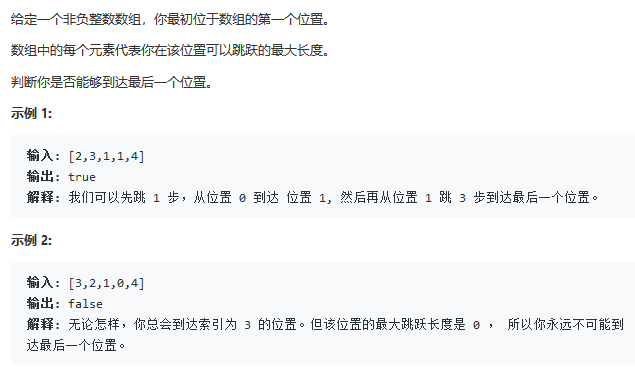
2. way of thinking

This problem is to consider whether we can reach the last position. When we reach each subscript, we can maintain a maximum subscript value to determine whether we can reach the last subscript of the array.

3. code

    public boolean canJump(int[] nums) {
        int maxIndex = 0;
        for (int i = 0; i < nums.length; i++) {
            // If the maximum subscript value is greater than the current traversal subscript value, then the subscript cannot be reached
            if (maxIndex < i) {
                return false;
            }

            // Update up to maximum subscript value
            maxIndex = Math.max(maxIndex, i + nums[i]);

            // If the maximum subscript value is not less than the maximum subscript value of the array, then the last position can be reached
            if (maxIndex >= nums.length - 1) {
                return true;
            }
        }

        return false;
    }

4. Operation results

45. Jump Game II

1. topic

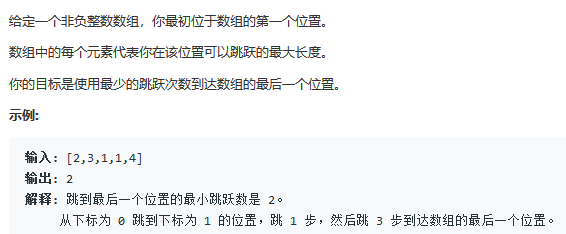
2. method 1

2.1 way of thinking

The difference between this question and the previous one is that this is to find the minimum number of times that can be reached. A more stupid method is that we can maintain an array to record the minimum number of times that can reach each subscript, traverse each subscript from the beginning to the end, update the minimum number of times that the subscript can reach, and finally calculate the minimum number of times that the last position of the array can reach. The idea requires an extra array, with a space complexity of o(n). In terms of time, it needs to traverse once from beginning to end. At the same time, each node needs to update the value of the subscript position it can reach, so the time complexity is O(n ²)

2.2 code

   public int jump(int[] nums) {
        int[] dp = new int[nums.length];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Integer.MAX_VALUE;
        }

        for (int i = 0; i < nums.length; i++) {
            for (int j = 1; j <= nums[i] && i + j < nums.length; j++) {
                dp[i + j] = Math.min(dp[i + j], dp[i] + 1);
            }
        }

        return dp[nums.length - 1];
    }

2.3 operation results

3. method two

3.1 way of thinking

The above method is simple, but time complexity is relatively high. We consider other methods.
We can think of the first question of Jump Game. The first question is whether we can reach the last subscript, that is, we have also found that we can reach the maximum subscript, so we can also consider this question as follows: we need to find out the minimum steps to reach the end of several groups, that is, we can judge by finding the farthest way to reach in step n, that is, thinking Change to find out what the subscript position we can reach for each additional step and whether we have reached the end of the array. This idea only needs to traverse the array once, and the space complexity is O(n).

3.2 code

    public int jump1(int[] nums) {
        // Steps of jumping
        int steps = 0;
        // The maximum subscript that the current step can reach
        int maxIndex = 0;
        // Add the maximum subscript that can be reached in one step
        int nextIndex = nums[0];
        
        for (int i = 0; i < nums.length; i++) {
            // The index value of the current traversal has exceeded the maximum index of the current steps
            if (i > maxIndex) {
                steps++;
                if (nextIndex >= nums.length - 1) {
                    break;
                } else {
                    maxIndex = nextIndex;
                }
            }

            // Update the next step to reach the maximum subscript
            nextIndex = Math.max(nextIndex, i + nums[i]);
        }

        return steps;
    }

3.3 operation results

It can be seen that the time required is far less than method one.

1306. Jump Game III

1. topic

2. way of thinking

This question is more interesting. It is to judge whether it can finally reach the subscript of element value 0 starting from a subscript of array. This kind of problem is easy to associate with the idea of recursion.

3. code

    private HashSet<Integer> set = new HashSet<>();

    public boolean canReach(int[] arr, int index) {
        // If the subscript already exists in set, it means that there is a loop and exit
        if (index < 0 || index > arr.length - 1 || set.contains(index)) {
            return false;
        }

        set.add(index);
        // Determine whether this point is the place with a subscript value of 0, or whether index + arr[index] and index - arr[index] are the place with a subscript value of 0
        if (arr[index] == 0 || canReach(arr, index + arr[index]) || canReach(arr, index - arr[index])) {
            return true;
        }
        set.remove(index);
        return false;
    }

4. Operation results

Related links

The github link of this code -- 55. Jump Game
github link of this code -- 45. Jump Game II
github link of this code -- 1306. Jump Game III
Other LeetCode topics
Leetcode top 100 raised questions