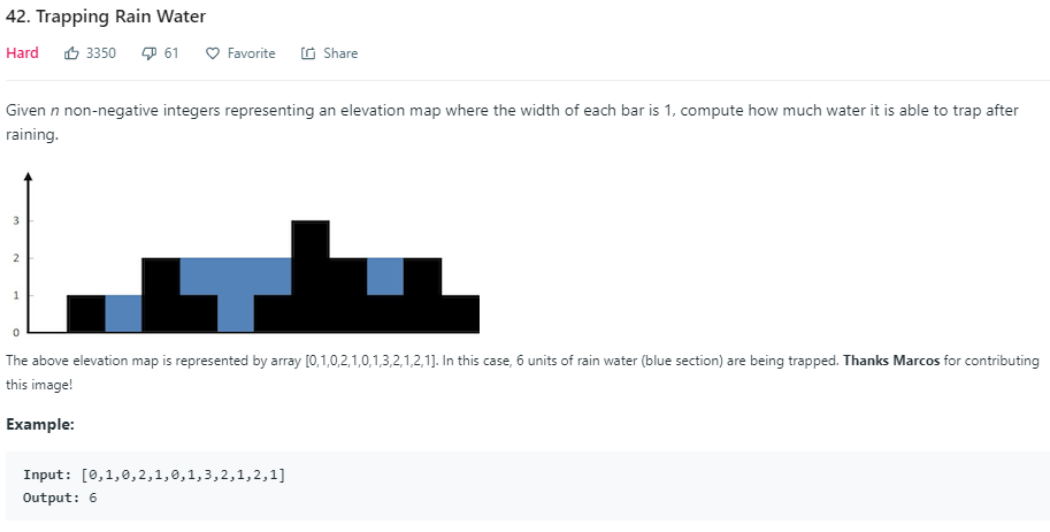
simple solution

Search from the left side of the list, and define left=0. If the number on the right side is less than the number on the left side, search from the left side to the right side until a number on the right side is greater than the number on the left side, or greater than the number after the left side. Otherwise, left+1

class Solution:
    def trap(self, height):   
        output = 0
        left = 0
        while left<len(height)-1:
            right = left+1
            if height[right]>=height[left]:
                left+=1
                continue
            else: 
                r = right
                s = height[right]
                while right<len(height)-1 and height[right]<height[left]:
                    right +=1
                    if height[right]>s:
                        s = height[right]
                        r = right
                if height[right]< height[left] and r==left+1:
                    left = r
                    continue
                elif height[right]< height[left]:
                    right  = r
                line = min(height[left],height[right])
                for i in range(left+1,right):
                    output +=  line - height[i]
                    left =right           
        return output

inorder traversal

Construct two lists, left-hand list and right-hand list, which respectively represent the maximum number of traversal from left / right before each position, and then subtract the number of current positions from the minimum number of two lists at the same position to get the number of water at the current position.

class Solution:
    def trap(self, height):
        arr, left, right, water = [], 0, 0, 0
        for i in height:
            left = max(left, i)
            arr.append(left)
        arr.reverse()
        for n, i in enumerate(reversed(height)):
            right = max(right, i)
            water += min(arr[n], right) - i
        return water

fast algorithm

Define left and right respectively to record the maximum number of simultaneous traversals on the left and right sides. When traversing on the left, if the maximum number on the right is greater than or equal to the left, and the number of traversal positions is less than the left, it means that there is water in the position. The same is true for the right.

class Solution:
    def trap(self, height):
        left = right = water = 0
        i, j = 0, len(height)-1
        while i <= j:
            left, right = max(left, height[i]), max(right, height[j])
            while i <= j and height[i] <= left <= right:
                water += left - height[i]
                i += 1
            while i <= j and height[j] <= right <= left:
                water += right - height[j]
                j -= 1
        return water