So far, I have written more than 600 algorithm problems, some of which have been sorted into pdf documents. At present, there are more than 1000 pages (and will continue to increase), which can be downloaded for free
Download link: https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
Extraction code: 6666

We talked about it earlier 520, backtracking algorithm to solve match square , similar to this question, you can see the details. Question 520 can be considered to separate the array into 4 elements and equal subsets, while this question is to separate the array into 2 elements and equal subsets. If the amount of data is small, the answer to question 520 will be the answer to this question by slightly modifying it, but if the amount of data is large, it will timeout. Therefore, this problem can not be solved by backtracking algorithm. We can use dynamic programming.

This question determines whether to divide the array into two parts and whether the elements and of the two parts are equal. First, we need to calculate the sum of all elements in the array, and then judge whether the sum is even:
If it is not an even number, it indicates that it is impossible to split into two exactly equal copies, and false is returned directly.

If it is an even number, we only need to judge whether the sum of some elements is equal to sum/2. If it is equal to sum/2, the rest must be equal to sum/2, indicating that we can divide the array into elements and equal parts.

Then the problem becomes clear at this time. Assuming sum/2 is the capacity of a backpack, we only need to find some elements and put them into the backpack. If the maximum sum of the elements in the backpack is equal to sum/2, it means that we can divide the array into two equal parts. This is the classic 0-1 knapsack problem. I told you before 371, knapsack problem series - Basic knapsack problem , you can see the details. I won't repeat the introduction here. Let's look for his recurrence formula and define dp[i][j] to represent the maximum value obtained by putting the ith item into the backpack with capacity j.

The value of the ith item is nums[i-1]:
If nums [I-1] > J, it means that the backpack capacity is insufficient and the i-th item cannot be put in, so we can't select the i-th item, then
dp[i][j]=dp[i-1][j]；

If nums [I-1] < = J, it means that the j-th item can be put into the backpack. We can choose to put it or not. Just take the maximum value. If you put it, it will occupy part of the backpack capacity. The maximum value is

dp[i][j]=dp[i-1][j-nums[i-1]]+nums[i-1]

If not
dp[i][j]=dp[i-1][j]；
Take the maximum of both

The final recurrence formula is as follows

if (j >= nums[i - 1]) {
    dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - nums[i - 1]] + nums[i - 1]);
} else {
    dp[i][j] = dp[i - 1][j];
}

Let's look at the final code

public boolean canPartition(int[] nums) {
    //Calculates the sum of all elements in the array
    int sum = 0;
    for (int num : nums)
        sum += num;
    //If sum is an odd number, it means that the array cannot be divided into two exactly equal parts
    if ((sum & 1) == 1)
        return false;
    //sum divided by 2
    int target = sum >> 1;
    int length = nums.length;
    int[][] dp = new int[length + 1][target+1];
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            //The following is a recursive formula
            if (j >= nums[i - 1]) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - nums[i - 1]] + nums[i - 1]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    //Determine whether the maximum backpack can store and target elements
    return dp[length][target] == target;
}

We can also write that the two-dimensional array dp is of boolean type. dp[i][j] indicates whether the sum of the first I elements in the array can form a sum of j. obviously, dp[0][0]=true indicates that the first 0 elements (that is, no elements) can form a sum of 0. The code is as follows

public boolean canPartition(int[] nums) {
    //Calculates the sum of all elements in the array
    int sum = 0;
    for (int num : nums)
        sum += num;
    //If sum is an odd number, it means that the array cannot be divided into two exactly equal parts
    if ((sum & 1) == 1)
        return false;
    //sum divided by 2
    int target = sum >> 1;
    int length = nums.length;
    boolean[][]dp = new boolean[length + 1][target+1];
    dp[0][0] = true;//base case
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            //Recurrence formula
            if (j >= nums[i - 1]) {
                dp[i][j] = (dp[i - 1][j] || dp[i-1][j - nums[i - 1]]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[length][target];
}

We can see that the current value of the above two-dimensional array is only related to the above line, so we can change it to one-dimensional. Note that the second for loop should be flashed back, otherwise the previous value will be overwritten, resulting in an error in the result. Take a closer look
dp[j] = (dp[j] || dp[j - nums[i - 1]]);
It is clear that the value after the same line depends on the previous one. If it is not flashback, the previous value will be modified, which will lead to an error in the calculation. Let's look at the code.

public boolean canPartition(int[] nums) {
    //Calculates the sum of all elements in the array
    int sum = 0;
    for (int num : nums)
        sum += num;
    //If sum is an odd number, it means that the array cannot be divided into two exactly equal parts
    if ((sum & 1) == 1)
        return false;
    //sum divided by 2
    int target = sum >> 1;
    int length = nums.length;
    boolean[] dp = new boolean[target + 1];
    dp[0] = true;//base case
    for (int i = 1; i <= length; i++) {
        //Be careful here j to flashback
        for (int j = target; j >= 1; j--) {
            //Recurrence formula
            if (j >= nums[i - 1]) {
                dp[j] = (dp[j] || dp[j - nums[i - 1]]);
            }
            //else {/ / omitted here
            //   dp[j] = dp[j];
            //}
        }
    }
    return dp[target];
}

DFS resolution

Each element can be selected or not. We only need to judge whether the sum of elements in all possible combinations is equal to sum/2. We can regard it as a binary tree. The left child node indicates to select the current element, and the right child node indicates not to select the current element, as shown in the figure below. The orange node indicates to select the current element, and the blue node indicates not to select.

Let's look at the code

public boolean canPartition(int[] nums) {
    //Calculates the sum of all elements in the array
    int sum = 0;
    for (int num : nums)
        sum += num;
    //If sum is an odd number, it means that the array cannot be divided into two exactly equal parts
    if ((sum & 1) == 1)
        return false;
    return dfs(nums, sum >> 1, 0);
}


private boolean dfs(int[] nums, int target, int index) {
    //If targe is equal to 0, it indicates that the sum of some elements is equal to sum/2, and returns true directly
    if (target == 0)
        return true;
    //If all array elements are found, or the target is less than 0, false is returned directly
    if (index == nums.length || target < 0)
        return false;
    //Select the current element or not
    return dfs(nums, target - nums[index], index + 1)
            || dfs(nums, target, index + 1);
}

Unfortunately, too much computation will lead to running timeout. We can optimize it and take a look at the code

public boolean canPartition(int[] nums) {
    //Calculates the sum of all elements in the array
    int sum = 0;
    for (int num : nums)
        sum += num;
    //If sum is an odd number, it means that the array cannot be divided into two exactly equal parts
    if ((sum & 1) == 1)
        return false;
    //sum divided by 2
    int target = sum >> 1;
    Boolean[][] map = new Boolean[nums.length][target + 1];
    return dfs(nums, 0, target, map);
}

private boolean dfs(int[] nums, int index, int target, Boolean[][] map) {
    //If targe is equal to 0, it indicates that the sum of some elements is equal to sum/2, and returns true directly
    if (target == 0)
        return true;
    //If all array elements are found, or the target is less than 0, false is returned directly
    if (index == nums.length || target < 0)
        return false;
    //Get from map
    if (map[index][target] != null)
        return map[index][target];
    //Select current element
    boolean select = dfs(nums, index + 1, target - nums[index], map);
    //Unselect current element
    boolean unSelect = dfs(nums, index + 1, target, map);
    //As long as one is true, it returns true; otherwise, it returns false
    if (select || unSelect) {
        map[index][target] = true;
        return true;
    }
    map[index][target] = false;
    return false;
}

Bit operation solution

Bit operation can be used here. The key lies in some restrictions in the problem, such as

• A non empty array of positive integers,
• No more than 100 elements in each array,
• The size of the array will not exceed 200, etc.

The principle is very simple. We only need to apply for an array bits[sum+1] with the size of sum+1 , the numbers in the array can only be 0 and 1. We can think of it as a very long binary bit. Because the int and long types are too short, we use the array here. Then, every time we traverse an element in the array, such as m, move the binary bit to the left by M bits, and then perform or operation with the original binary bit. Finally, judge bits[sum/2] Whether it is 1. If it is 1, it returns true. The text description is not very direct. Let's take example 1 as an example to draw a diagram

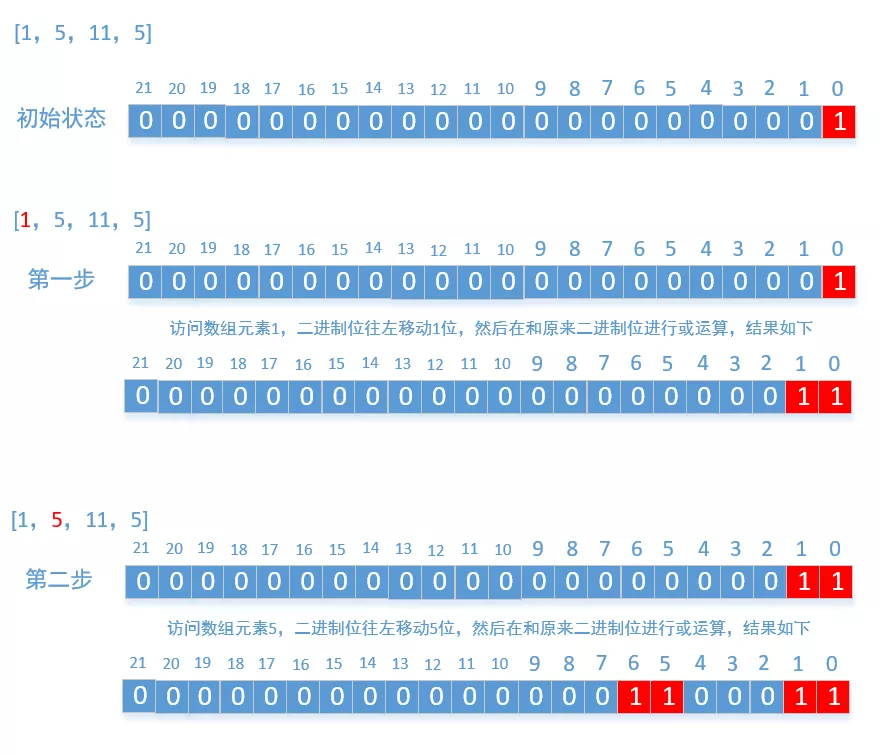
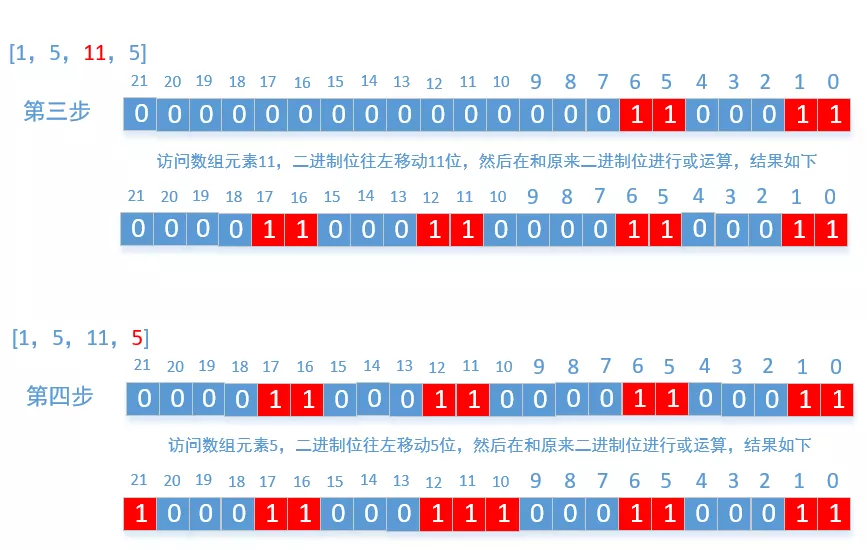
Finally, you will find a rule that as long as the position of the final operation is 1, it can be combined with the elements in the array. As long as it is 0, it can not be combined with the elements in the array. After understanding the above process, the code is easy to write. Because we only need to judge whether the value in the middle of the binary bit is 1, so we only need to calculate the low value Bit, the high bit does not need to be calculated at all, because it moves to the left, and the high bit will not have any impact on the middle value, so we can do some optimization here, and finally look at the code

public boolean canPartition(int[] nums) {
    //Calculates the sum of all numbers in the array
    int sum = 0;
    for (int n : nums)
        sum += n;
    //If sum is an odd number, return false directly
    if ((sum & 1) == 1)
        return false;
    int len = sum >> 1;
    //Here, the length of bits is len+1, because we only need to calculate
    //Just the low order. There's no need to calculate all the values
    byte[] bits = new byte[len + 1];
    bits[0] = 1;
    for (int i = 0; i < nums.length; i++) {
        int num = nums[i];
        int size = len - num;
        for (int j = size; j >= 0; j--) {
            bits[j + num] |= bits[j];
        }
        //If the median judgment is 1, it indicates that it can be divided into two equal types
        //Subset, directly return true, and no further calculation is required
        if ((bits[len] & 1) != 0)
            return true;
    }
    return false;
}