leetcode 11 Pruning & backtracking
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
prune
Exclude branches that do not meet the criteria. Improve the running efficiency of the program.
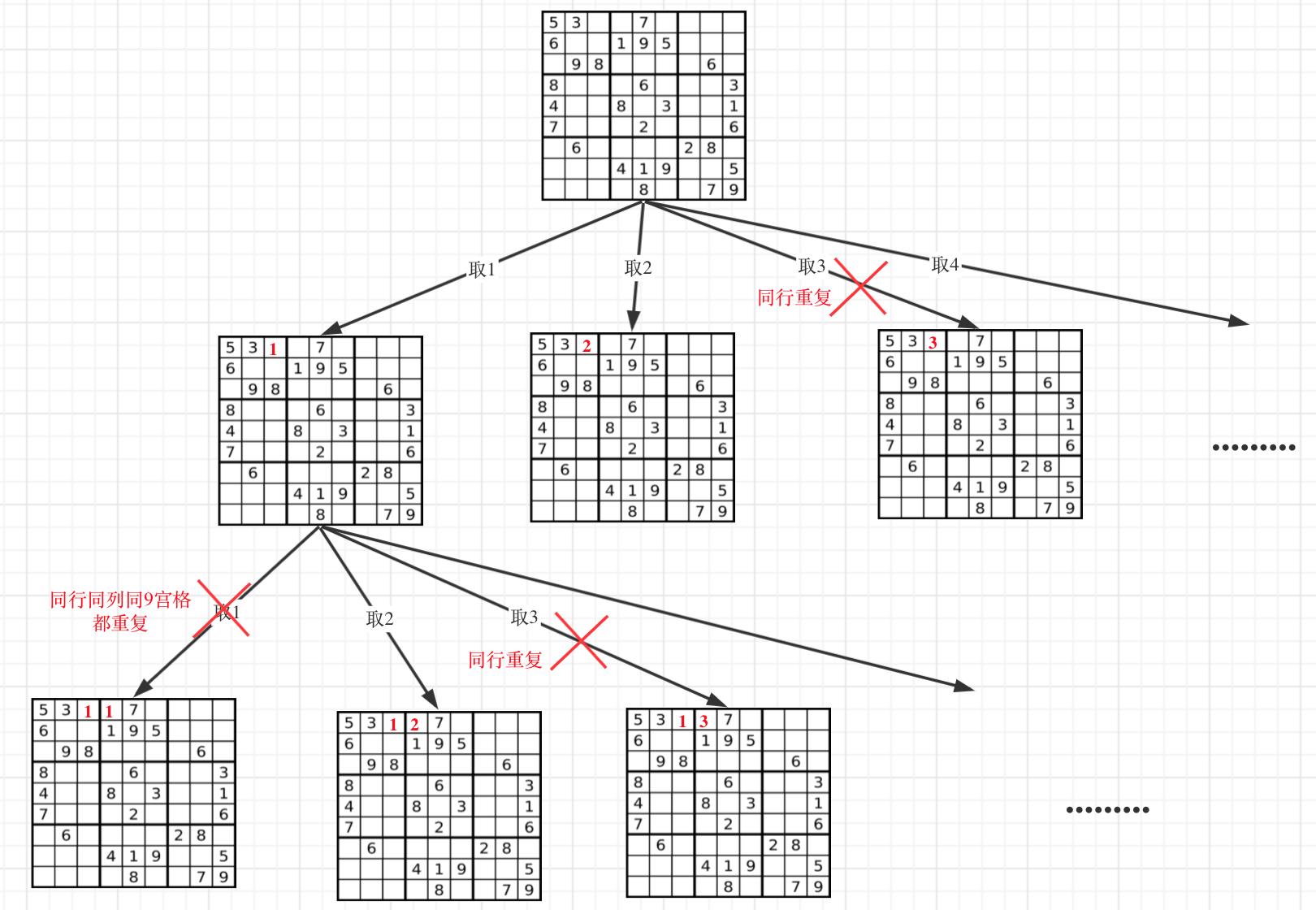
to flash back:
Layer by layer recursion, trying to find prime answers,
- Find the answer: return the result and try another branch
- No answer found: go back to the previous level and try another branch
Backtracking template:
result = [];
function backtrack (path, list) {
if (Meet the conditions) {
result.push(path);
return
}
for () {
// Single layer logic
backtrack (path, list)
// Deselect reset status
}
}Retrospective Trilogy:
- Backtracking parameters
- Termination conditions
- Single layer recursive logic
- Select another branch (deselect reset status)
22. Bracket generation (medium)
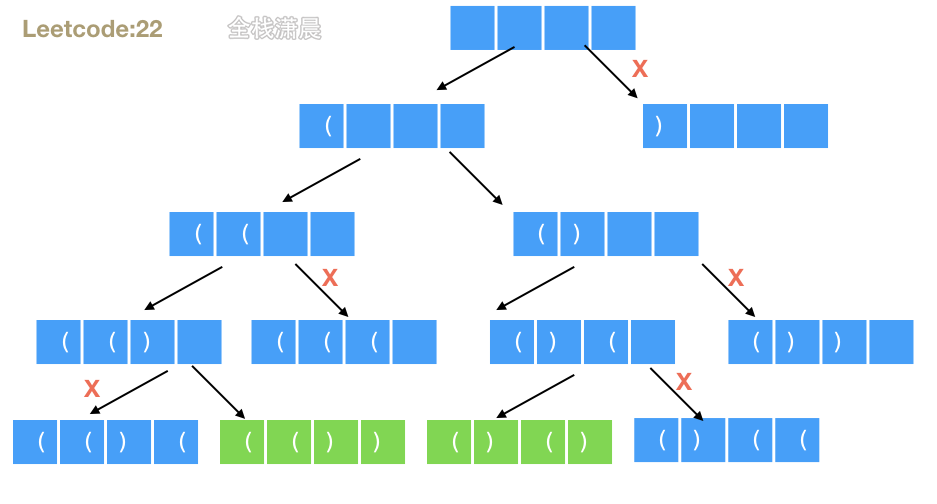
Method 1: Violence
Complexity analysis: the time complexity is O(2^2n*n). The length of the string is 2n. There are two options for each position. Select the left or right parenthesis to verify whether the string is valid. The complexity is O(n). It will be optimized after pruning. The worst case is O(2^2n*n). Space complexity O(n), maximum number of recursion 2n
Method 2. Recursive dfs
- Idea: recursion is adopted. The termination condition is that the length of the string is equal to 2n. The recursive function passes in the constructed string. There are two options for how many left and right parentheses are left. Select the left or right parentheses. Pruning optimization can be carried out here. The right parentheses can be selected only if the holding number of the right parentheses is greater than the holding number of the left parentheses. Otherwise, it must not constitute valid parentheses
Js:
const generateParenthesis = (n) => {
const res = []; // Output result array
const generate = (str, left, right) => {
if (str.length == 2 * n) { // String build complete
res.push(str); // Add string to res
return; // End current recursion (end current search branch)
}
if (left > 0) { // As long as the left parenthesis is left, you can choose it and continue to choose recursively
generate(str + '(', left - 1, right);
}
if (right > left) { // The right bracket can only be selected if the holding quantity of the right bracket is greater than the holding quantity of the left bracket
generate(str + ')', left, right - 1);
}
};
generate('', n, n); // The entry of recursion. The initial string is an empty string, and the number of initial parentheses is n
return res;
};Java:
class Solution {
List<String> res = new ArrayList<>();
public List<String> generateParenthesis(int n) {
generate(n, n, "");
return res;
}
private void generate(int left, int right, String curStr) {
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
if (left > 0) {
generate(left - 1, right, curStr + "(");
}
if (right > left) {
generate(left, right - 1, curStr + ")");
}
}
}Method 3. Backtracking
- Idea: when there are too many left parentheses, it means that the number of left parentheses in the string is less than that of right parentheses, which is illegal. Try to add left parentheses to the string, and then backtrack, try to add right parentheses, and then try backtracking
Js:
var generateParenthesis = function(n) {
if (n == 0) return []
const res = []
let track = []
backtrack(n, n, track, res)
return res
function backtrack(left, right, track, res) {
// Quantity less than 0, illegal
if (left < 0 || right < 0) return
// If there are too many left parentheses, it indicates that it is illegal
if (right < left) return
// All parentheses are used up to get a legal combination
if (left == 0 && right == 0) {
res.push(track.join(''))
return
}
// Try adding an open parenthesis
track.push('(')
//In this place, you must pay attention to copying a track, that is, [... Track], otherwise it will affect other branches
backtrack(left - 1, right, [...track], res)
track.pop()
// Try adding a closing bracket
track.push(')')
backtrack(left, right - 1, [...track], res)
track.pop()
}
};Java:
class Solution {
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<String>();
backtrack(res, new StringBuilder(), 0, 0, n);
return res;
}
public void backtrack(List<String> res, StringBuilder cur, int left, int right, int max) {
if (cur.length() == max * 2) {
res.add(cur.toString());
return;
}
if (left < max) {
cur.append('(');
backtrack(res, cur, left + 1, right, max);
cur.deleteCharAt(cur.length() - 1);
}
if (right < left) {
cur.append(')');
backtrack(res, cur, left, right + 1, max);
cur.deleteCharAt(cur.length() - 1);
}
}
}51. Queen n (hard)
Method 1. Backtracking
The animation is too large. Click to view it
- Idea: traverse the chessboard from top to bottom and from left to right, prepare three sets to record the coordinates that can be attacked by the column and two diagonals respectively, try to place the queen in each empty space, update the coordinates of the three sets that can be attacked after placement, and then continue to traverse the next layer. After completing the next layer, try to trace back to the current layer, that is, cancel the queen placed in the current layer, At the same time, undo the three set coordinates that can be attacked, and keep backtracking until the traversal is completed to find all possible solutions.
- Complexity analysis: time complexity: O(N!), where N is the number of queens. Since each queen must be in a different column, the column of placed queens cannot place other queens. The first queen has N columns to choose from, and the second queen has at most N-1 columns to choose from. Spatial complexity: O(N), where N is the number of queens. The spatial complexity mainly depends on the number of recursive call layers, the array recording the subscripts of Queen columns placed in each row and three sets. The number of recursive call layers will not exceed N, the length of the array is N, and the number of elements in each set will not exceed N.
js:
const solveNQueens = (n) => {
const board = new Array(n);
for (let i = 0; i < n; i++) {
board[i] = new Array(n).fill('.');//Generate board
}
const cols = new Set(); // A column set that records the columns where queens have occurred
const diag1 = new Set(); // Diagonal set
const diag2 = new Set(); // Inverse diagonal set
const res = [];//Result array
const backtrack = (row) => {
if (row == n) {//Termination conditions
const stringsBoard = board.slice();
for (let i = 0; i < n; i++) {//Generate string
stringsBoard[i] = stringsBoard[i].join('');
}
res.push(stringsBoard);
return;
}
for (let col = 0; col < n; col++) {
// If there is no queen in the column and diagonal of the current point, you can select it. Otherwise, skip
if (!cols.has(col) && !diag1.has(row + col) && !diag2.has(row - col)) {
board[row][col] = 'Q'; // Place queen
cols.add(col); // The Queen's column is recorded
diag2.add(row - col); // The record shows the Queen's diagonal
diag1.add(row + col); // The record puts the Queen's negative diagonal
backtrack(row + 1);
board[row][col] = '.'; // Undo the queen of the point
cols.delete(col); // Delete the corresponding records
diag2.delete(row - col);
diag1.delete(row + col);
}
}
};
backtrack(0);
return res;
};java:
class Solution {
public List<List<String>> solveNQueens(int n) {
List<List<String>> res = new ArrayList<List<String>>();
int[] queens = new int[n];
Arrays.fill(queens, -1);
Set<Integer> cols = new HashSet<Integer>();
Set<Integer> diag1 = new HashSet<Integer>();
Set<Integer> diag2 = new HashSet<Integer>();
backtrack(res, queens, n, 0, cols, diag1, diag2);
return res;
}
public void backtrack(List<List<String>> res, int[] queens, int n, int row, Set<Integer> cols, Set<Integer> diag1, Set<Integer> diag2) {
if (row == n) {
List<String> board = generateBoard(queens, n);
res.add(board);
} else {
for (int i = 0; i < n; i++) {
if (cols.contains(i)) {
continue;
}
int diagonal1 = row - i;
if (diag1.contains(diagonal1)) {
continue;
}
int diagonal2 = row + i;
if (diag2.contains(diagonal2)) {
continue;
}
queens[row] = i;
cols.add(i);
diag1.add(diagonal1);
diag2.add(diagonal2);
backtrack(res, queens, n, row + 1, cols, diag1, diag2);
queens[row] = -1;
cols.remove(i);
diag1.remove(diagonal1);
diag2.remove(diagonal2);
}
}
}
public List<String> generateBoard(int[] queens, int n) {
List<String> board = new ArrayList<String>();
for (int i = 0; i < n; i++) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[queens[i]] = 'Q';
board.add(new String(row));
}
return board;
}
}52. N Queen II(hard)
Method 1. Bit operation

js:
var totalNQueens = function (n) {
if (n < 1) return
let count = 0;
dfs(n, 0, 0, 0, 0)
return count
//n: Number of queens
//Row: current row
//cols: where to place the queen
//diag1: left diagonal that can be attacked
//diag2: right diagonal that can be attacked
function dfs(n, row, cols, diag1, diag2) {
if (row >= n) {//Recursive termination statistical solution
count += 1;
return
}
//~(cols | diag1 | diag2): after the attack positions are reversed, the position of 1 is the position where the queen can be placed
//(1 < < n) - 1: from right to left, positions greater than n become 0
//(~ (cols | diag1 | diag2)) & ((1 < < n) - 1): the queen can be placed from right to left, and the positions greater than n become 0
let bits = (~(cols | diag1 | diag2)) & ((1 << n) - 1)
while (bits) {
let p = bits & -bits//Take the first 1 from right to left
bits = bits & (bits - 1)//Remove the first 1 from right to left
//Column and two diagonals are closed with non placeable bits
dfs(n, row + 1, cols | p, (diag1 | p) << 1, (diag2 | p) >>> 1)
}
}
};Java:
class Solution { public int totalNQueens(int n) { return dfs(n, 0, 0, 0, 0); } public int dfs(int n, int row, int clos, int diag1, int diag2) { if (row == n) { return 1; } else { int count = 0; int bits = ((1 << n) - 1) & (~(clos | diag1 | diag2)); while (bits != 0) { int position = bits & (-bits); bits = bits & (bits - 1); count += dfs(n, row + 1, clos | position, (diag1 | position) << 1, (diag2 | position) >> 1); } return count; } }}36. Effective Sudoku (medium)
Method 1: backtracking
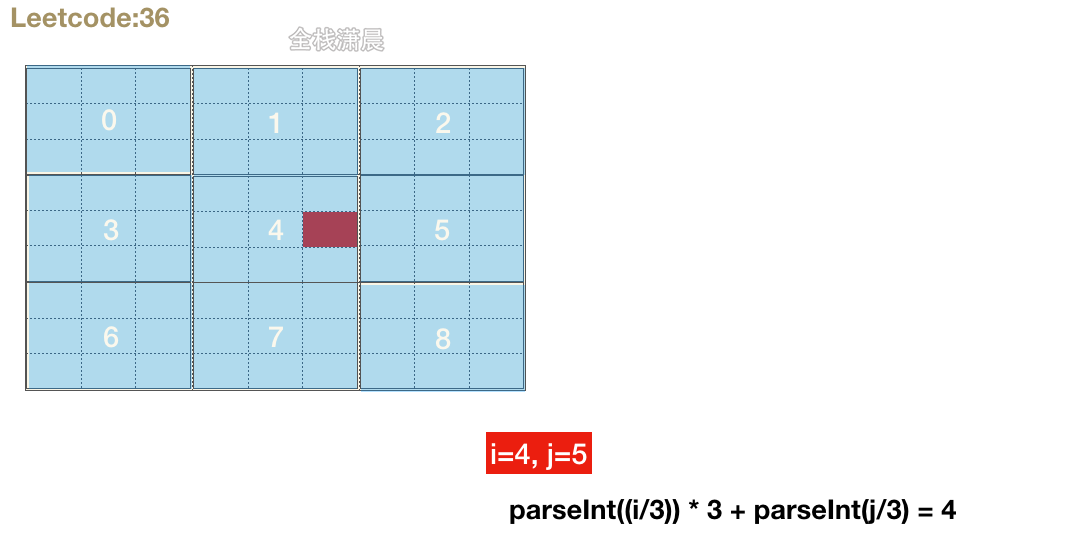
- Idea: prepare rows, columns, 3 * 3 small blocks, three hash tables or sets or two-dimensional arrays of 9 * 9. As long as you can judge repetition, cycle from top to bottom and from left to right. Check whether there are duplicate numbers in rows, columns and 3 * 3 small blocks in turn. If so, return to false, and then update the hash table or set.
- Complexity analysis: time complexity: O(1). Sudoku has 81 cells, and each cell can be traversed once. Space complexity: O(1). The size of Sudoku is fixed, so the space of hash table is also fixed.
Js:
var isValidSudoku = function(board) {
// Direction weight judgment
let rows = {};//that 's ok
let columns = {};//column
let boxes = {};//3 * 3 small square
// Ergodic Sudoku
for(let i = 0;i < 9;i++){
for(let j = 0;j < 9;j++){
let num = board[i][j];
if(num != '.'){//A valid number was encountered
let boxIndex = parseInt((i/3)) * 3 + parseInt(j/3);// Sub Sudoku serial number
if(rows[i+'-'+num] || columns[j+'-'+num] || boxes[boxIndex+'-'+num]){//Repeated detection
return false;
}
// Direction + number form a unique key value. If it occurs for the second time, it is a repetition
// Update three objects
rows[i+'-'+num] = true;
columns[j+'-'+num] = true;
boxes[boxIndex+'-'+num] = true;
}
}
}
return true;
};Java:
class Solution {
public boolean isValidSudoku(char[][] board) {
int[][] rows = new int[9][9];//The same is true with arrays
int[][] columns = new int[9][9];
int[][][] boxes = new int[3][3][9];
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
char c = board[i][j];
if (c != '.') {
int index = c - '0' - 1;
rows[i][index]++;
columns[j][index]++;
boxes[i / 3][j / 3][index]++;
if (rows[i][index] > 1 || columns[j][index] > 1 || boxes[i / 3][j / 3][index] > 1) {
return false;
}
}
}
}
return true;
}
}37. Solving Sudoku(hard)
- Idea: cycle rows and columns, try to place 1-9 in each position, and test the legitimacy, including the legitimacy of rows, columns and 3 * 3 blocks. If it is legal, continue to cycle until a legal solution is found. If it is not legal, go back to the state and continue to try other possibilities
- Complexity analysis: the same as question 36
js:
var solveSudoku = function(board) {
function isValid(row, col, val, board) {
let len = board.length
// The number in the row cannot be repeated
for(let i = 0; i < len; i++) {
if(board[row][i] === val) {
return false
}
}
// The number in the column cannot be repeated
for(let i = 0; i < len; i++) {
if(board[i][col] === val) {
return false
}
}
let startRow = Math.floor(row / 3) * 3
let startCol = Math.floor(col / 3) * 3
//The number in the box cannot be repeated
for(let i = startRow; i < startRow + 3; i++) {
for(let j = startCol; j < startCol + 3; j++) {
if(board[i][j] === val) {
return false
}
}
}
return true
}
function backTracking() {//Backtracking function
for(let i = 0; i < board.length; i++) {
for(let j = 0; j < board[0].length; j++) {//Loop rows and columns
if(board[i][j] !== '.') continue
for(let val = 1; val <= 9; val++) {//Try placing 1-9 in the current cell
if(isValid(i, j, `${val}`, board)) {//Judge the legitimacy of placed numbers
board[i][j] = `${val}`//Place number
if (backTracking()) {//Legal return
return true
}
board[i][j] = `.`//Illegal backtracking status
}
}
return false//The numbers from 1 to 9 are illegal, and false is returned
}
}
return true//All possibilities are tried to complete. Returning true indicates that there is a solution
}
backTracking()
return board
};Java:
class Solution {
public void solveSudoku(char[][] board) {
backTracking(board);
}
private boolean backTracking(char[][] board){
for (int i = 0; i < 9; i++){ // Traversal row
for (int j = 0; j < 9; j++){ // Traversal column
if (board[i][j] != '.'){
continue;
}
for (char k = '1'; k <= '9'; k++){ //Try placing 1-9 in the current position
if (isValid(i, j, k, board)){
board[i][j] = k;//Place number
if (backTracking(board)){ //Legal return
return true;
}
board[i][j] = '.';
}
}
return false;//The numbers from 1 to 9 are illegal, and false is returned
}
}
return true;//All possibilities are tried to complete. Returning true indicates that there is a solution
}
private boolean isValid(int row, int col, char val, char[][] board){
// Whether peers repeat
for (int i = 0; i < 9; i++){
if (board[row][i] == val){
return false;
}
}
// Is the same column repeated
for (int j = 0; j < 9; j++){
if (board[j][col] == val){
return false;
}
}
// Whether the elements in the small box are repeated
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++){
for (int j = startCol; j < startCol + 3; j++){
if (board[i][j] == val){
return false;
}
}
}
return true;
}
}79. Word search(medium)
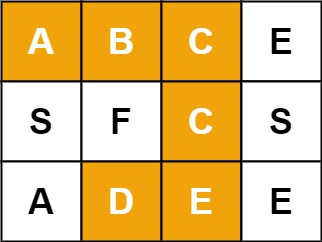
- Idea: traverse the grid from top to bottom and left to right. Each coordinate recursively calls the check (i,j, K) function. i,j represents the grid coordinates and K represents the k-th character of word. If the k-th character can be searched, return true, otherwise return false. There are two termination conditions for the check function
- If the characters at positions i and j are not equal to the characters at position k of the string, the search path fails and returns false
- If the search reaches the end of the string, a path in the grid is found, and the characters on this path can just form the string s
If both conditions are not satisfied, the current grid node is added to the visited array. Visited indicates that the node has been accessed, and then continue to try along the four directions of the current grid coordinates. If the substring starting from k is not found, the backtracking status visited[i] [j] = false and continue the subsequent attempt.
- Complexity analysis: the time complexity O(MN ⋅ 3^L), m and N are the length and width of the grid, and l is the length of the string word. When the check function is called for the first time, it is checked in four directions. The nodes of other coordinates are checked in three directions, and the branches that come will not go back in the opposite direction. Therefore, the time complexity of the check function is 3^L, while the grid has M*N coordinates, And pruning exists, so the time complexity in the worst case is O(MN ⋅ 3^L). The space complexity is O(MN), the visited array space is O(MN), and the maximum depth of the check recursive stack is O(MN) in the worst case
Method 1: backtracking
Js:
var exist = function(board, word) {
const h = board.length, w = board[0].length;//Length and width of grid
const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];//Direction array
const visited = new Array(h);//Indicates whether the array has been accessed
for (let i = 0; i < visited.length; ++i) {//Initialize visited array
visited[i] = new Array(w).fill(false);
}
const check = (i, j, s, k) => {//Check whether the substring composed of 0-k characters can be searched from grids i and j
//If the characters at positions i and j are not equal to the k-th character, the search path fails and returns false
if (board[i][j] != s.charAt(k)) {
return false;
//If the search reaches the end of the string, a path in the grid is found, and the characters on this path can just form the string s
} else if (k == s.length - 1) {
return true;
}
visited[i][j] = true;//Tags i, j have been accessed
let result = false;
for (const [dx, dy] of directions) {//Continue to try to find in the four directions of i and j
let newi = i + dx, newj = j + dy;
if (newi >= 0 && newi < h && newj >= 0 && newj < w) {//Legal check of new coordinate position
if (!visited[newi][newj]) {//New coordinates cannot exist in visited, that is, they cannot be accessed
const flag = check(newi, newj, s, k + 1);//Continue checking for new coordinates
if (flag) {//If a string is found in the grid, the loop is skipped
result = true;
break;
}
}
}
}
visited[i][j] = false;//Backtracking status
return result;//Return results
}
for (let i = 0; i < h; i++) {
for (let j = 0; j < w; j++) {
const flag = check(i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
};Java:
class Solution {
public boolean exist(char[][] board, String word) {
int h = board.length, w = board[0].length;
boolean[][] visited = new boolean[h][w];
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
boolean flag = check(board, visited, i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
}
public boolean check(char[][] board, boolean[][] visited, int i, int j, String s, int k) {
if (board[i][j] != s.charAt(k)) {
return false;
} else if (k == s.length() - 1) {
return true;
}
visited[i][j] = true;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
boolean result = false;
for (int[] dir : directions) {
int newi = i + dir[0], newj = j + dir[1];
if (newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length) {
if (!visited[newi][newj]) {
boolean flag = check(board, visited, newi, newj, s, k + 1);
if (flag) {
result = true;
break;
}
}
}
}
visited[i][j] = false;
return result;
}
}46. Full arrangement (medium)
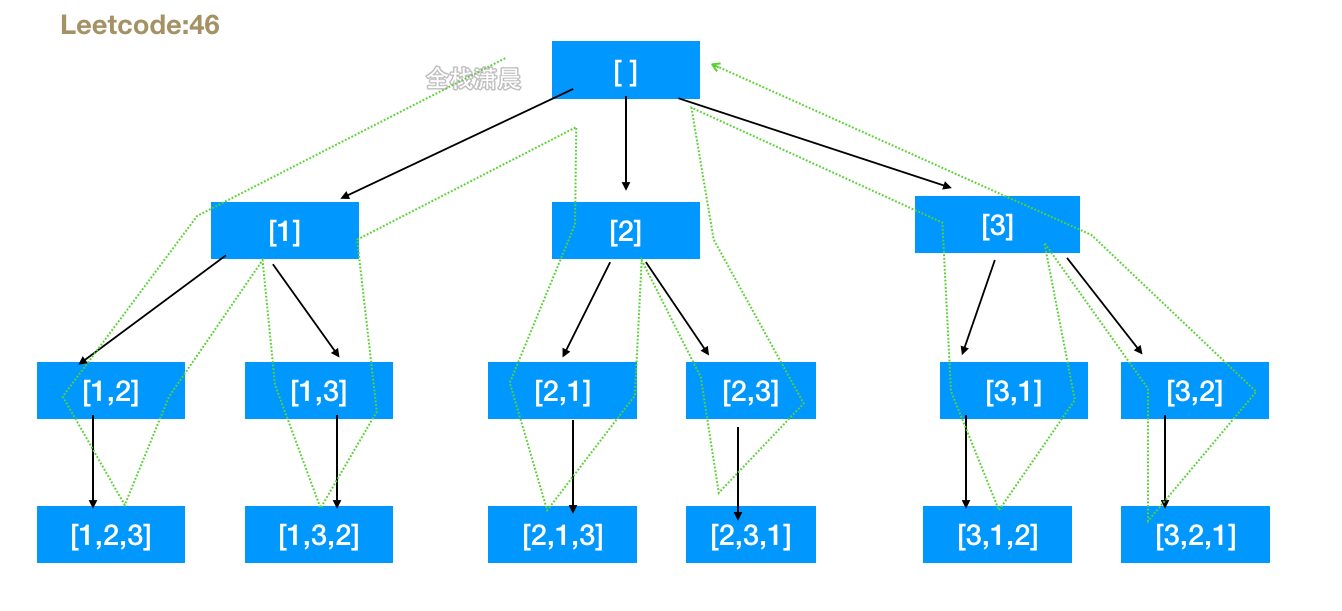
- Idea: prepare the path array, store the number arrangement in each backtracking recursive branch, call the backtracking function, pass in num, Num length, used array, used represents the number that has been used, loop the number in num in the backtracking function, add the elements in num to the path in each layer of loop, and then call the backtracking function recursively. After the call is completed, the state before backtracking, When the length of the path array is the same as that of nums, an arrangement is found.
- Complexity: time complexity O(n*n!). Space complexity O(n), recursive stack depth
js:
var permute = function(nums) {
const res = [], path = [];
backtracking(nums, nums.length, []);//Call the backtracking function to pass in num, Num length, and used array
return res;
function backtracking(n, k, used) {
if(path.length === k) {//Recursive termination condition
res.push(Array.from(path));
return;
}
for (let i = 0; i < k; i++ ) {
if(used[i]) continue;//Skip this cycle after it has been used
path.push(n[i]);
used[i] = true;
backtracking(n, k, used);//recursion
path.pop();//Backtracking pop s the element push ed in, then marks it as unused and continues to other branches
used[i] = false;
}
}
};java:
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0){
return result;
}
used = new boolean[nums.length];
permuteHelper(nums);
return result;
}
private void permuteHelper(int[] nums){
if (path.size() == nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
path.add(nums[i]);
permuteHelper(nums);
path.removeLast();
used[i] = false;
}
}
}77. Portfolio (medium)
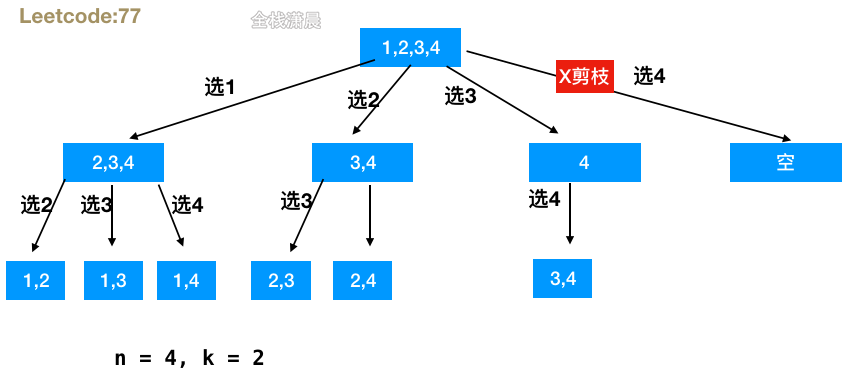
- Idea: the backtracking function passes in n, K and the selected element position startIndex. In each layer of recursion, start the cycle from startIndex to the position of n - (k - path.length) + 1, add these numbers to the path, then startIndex plus 1, continue the recursive function to enter the next branch, complete the backtracking state after the call, and terminate this layer of branch when the length of path is equal to K, Add to the results.
- Complexity: time complexity: O(C(n, k) * k). The total number of enumeration results is C(n, k). It takes O(k) time to get one result each time. Space complexity: O(n), the maximum is n-layer recursive stack.
js:
const combine = (n, k) => {
const res = [];
const helper = (startIndex, path) => { //startIndex indicates the starting position of the search (path is a combination of each branch)
if (path.length == k) {
res.push(path.slice()); //A copy is required to avoid being affected by other branches
return;
}
for (let i = startIndex; i <= n - (k - path.length) + 1; i++) {//prune
path.push(i); //Join path
helper(i + 1, path); //Next level recursion
path.pop(); //Backtracking status
}
};
helper(1, []); //Recursive entry
return res;
}java:
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
combineHelper(n, k, 1);
return result;
}
private void combineHelper(int n, int k, int startIndex){
if (path.size() == k){
result.add(new ArrayList<>(path));
return;
}
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
path.add(i);
combineHelper(n, k, i + 1);
path.removeLast();
}
}
}17. Letter combination of telephone number (medium)
Method 1.dfs + backtracking
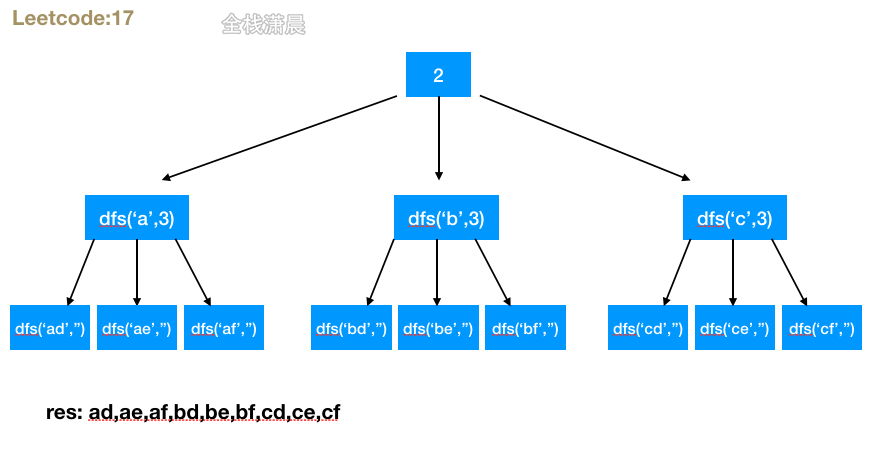
- Idea: depth first traversal. The traversal function passes in the string formed by each layer and a position pointer pointing to the character. When the position of the pointer reaches the end of the string, the formed string will be added to the result array. Each recursive layer traverses the characters corresponding to the numbers of this layer, and then passes in new characters. The pointer moves back once and recurses continuously
- Complexity: time complexity O(3^m * 4^n), m and N are the numbers corresponding to three letters and four letters respectively. Space complexity O(m+n), depth of recursive stack, max. m+n
js:
//Input: digits = "23"
//Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
var letterCombinations = (digits) => {
if (digits.length == 0) return [];
const res = [];
const map = {//Establish the mapping relationship between telephone numbers and letters
2: "abc",
3: "def",
4: "ghi",
5: "jkl",
6: "mno",
7: "pqrs",
8: "tuv",
9: "wxyz",
};
const dfs = (curStr, i) => {//curStr is the string of each recursive layer, and i is the scanned pointer
if (i > digits.length - 1) {//Boundary conditions, recursive exit
res.push(curStr); //The solution of one branch is pushed into res
return; //End the recursive branch and enter another branch
}
const letters = map[digits[i]]; //Take out the letter corresponding to the number
for (const l of letters) {
//Branch into different letters
dfs(curStr + l, i + 1); //Parameter, pass in a new string, i shift right and continue recursion
}
};
dfs("", 0); // Recursive entry, passing in an empty string, i the initial position of 0
return res;
};java:
class Solution {
String[] map = { " ", "*", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return new ArrayList<>();
}
dfs(digits, new StringBuilder(), 0);
return res;
}
List<String> res = new ArrayList<>();
void dfs(String digits, StringBuilder curStr, int index) {
if (index == digits.length()) {
res.add(curStr.toString());
return;
}
char c = digits.charAt(index);
int pos = c - '0';
String map_string = map[pos];
for (int i = 0; i < map_string.length(); i++) {
curStr.append(map_string.charAt(i));
dfs(digits, curStr, index + 1);
curStr.deleteCharAt(curStr.length() - 1);
}
}
}Method 2.bfs
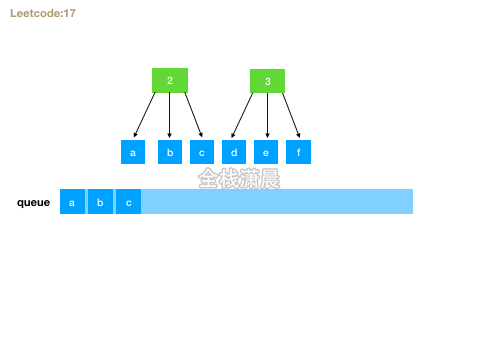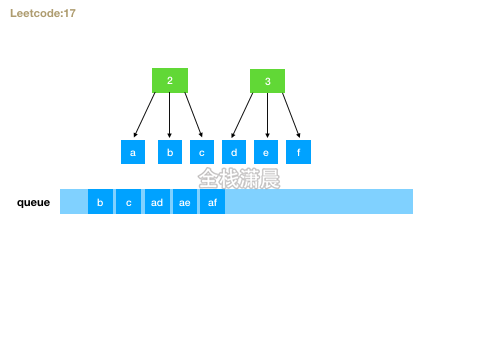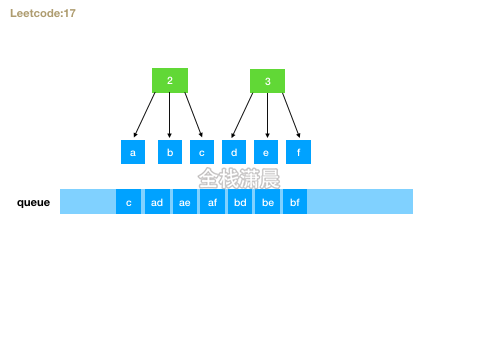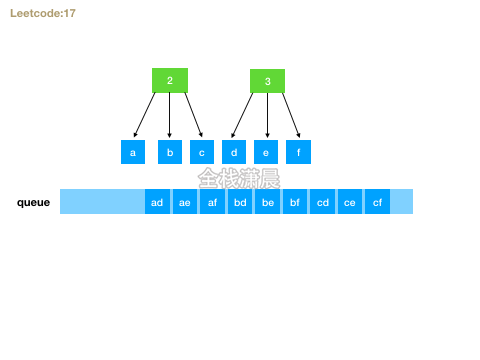
- Idea: use queue breadth first traversal. First cycle the number array, then take out the corresponding letters, form a new string with the string of the current layer, and add it to the queue. After traversal, the last layer of the queue is the solution.
- Complexity: time complexity O(3^m * 4^n), m and N are the number of arrays corresponding to three characters and four letters respectively. Space complexity O(3^m * 4^n). The maximum space size of the queue is 3^m * 4^n
js:
var letterCombinations = (digits) => {
if (digits.length == 0) return [];
const map = {
2: "abc",
3: "def",
4: "ghi",
5: "jkl",
6: "mno",
7: "pqrs",
8: "tuv",
9: "wxyz",
};
const queue = [];
queue.push("");
for (let i = 0; i < digits.length; i++) {//Loop each character of the number
const levelSize = queue.length; //Number of nodes in the current layer
for (let j = 0; j < levelSize; j++) {
const curStr = queue.shift(); //String of the current layer
const letters = map[digits[i]];//Gets the alphanumeric character corresponding to the number
for (const l of letters) {
queue.push(curStr + l); //The newly generated string is listed
}
}
}
return queue; //The string generated by the last layer is the solution
};java:
class Solution {
public List<String> letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return new ArrayList<String>();
}
String[] map = { " ", "*", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
List<String> res = new ArrayList<>();
res.add("");
for (int i = 0; i < digits.length(); i++) {
String letters = map[digits.charAt(i) - '0'];
int levelSize = res.size();
for (int j = 0; j < levelSize; j++) {
String tmp = res.remove(0);
for (int k = 0; k < letters.length(); k++) {
res.add(tmp + letters.charAt(k));
}
}
}
return res;
}
}78. Subset (medium)
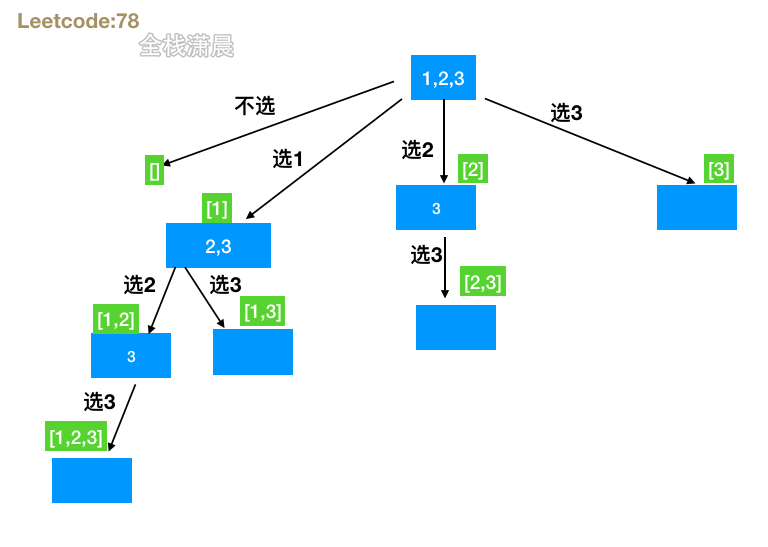
- Idea: the backtracking function passes in the startIndex at the beginning of the character and recurses continuously. The startIndex of each layer is increased by 1. When one branch ends, it starts backtracking and enters another branch.
- Complexity: time complexity O(n*2^n). As shown in the figure, the recursive states are 2^n states, and the complexity of constructing path array for each state is O(n). Space complexity O(n), that is, the space of recursive stack
js:
//Example: num = [1,2,3]
var subsets = function(nums) {
let result = []//Storage results
let path = []//Store the results of a branch
function backtracking(startIndex) {//The position at which the startIndex character recursion begins
result.push(path.slice())//path.slice() breaks the reference relationship with path
for(let i = startIndex; i < nums.length; i++) {//Recursion from startIndex
path.push(nums[i])//Current character push path
backtracking(i + 1)//startIndex moves backward one position to continue recursion
path.pop()//Backtracking status
}
}
backtracking(0)
return result
};java:
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
if (nums.length == 0){
result.add(new ArrayList<>());
return result;
}
backtracking(nums, 0);
return result;
}
private void backtracking(int[] nums, int startIndex){
result.add(new ArrayList<>(path));
if (startIndex >= nums.length){
return;
}
for (int i = startIndex; i < nums.length; i++){
path.add(nums[i]);
backtracking(nums, i + 1);
path.removeLast();
}
}
}473. Match square (medium)

- Idea: sort the nums array to reduce the number of backtracking. Keep trying to put the elements in nums into four buckets. If they can all be put down, they can be assembled into a square
js:
//Example: [1,2,2,2,1]
var makesquare = function (nums) {
function backtrack(i, nums, edge, bucket) {
if (i >= nums.length) {//Recursive end condition
return true;
}
for (let j = 0; j < 4; j++) {//Cycle 4 barrels
if (bucket[j] + nums[i] > edge) {//This bucket can't hold. Keep looking for the next bucket
continue;
}
bucket[j] += nums[i];//Adds the current element to the bucket
if (backtrack(i + 1, nums, edge, bucket)) {//Index i plus 1 continues to recurse the elements in the next nums
return true;//The next element can be put into the bucket
}
bucket[j] -= nums[i];//Backtracking status
}
return false;//If you don't put the proper bucket at the end of the cycle, it can't form a square
}
if (nums.length < 4) {//nums is less than 4 in length and cannot form a square directly
return false;
}
let sum = 0;
for (let i = 0; i < nums.length; i++) {
sum += nums[i];
}
if (sum % 4) {//The sum of nums cannot be divided by 4 and cannot form a square row
return false;
}
nums.sort((a, b) => b - a);//Sort nums
let bucket = Array(4).fill(0);//Prepare 4 barrels
return backtrack(0, nums, sum / 4, bucket);//The index i, num, a side length, and bucket of the passed in num element
};