1. topic

2. answers

2.1. Method I

stay LeetCode 108 -- transform an ordered array into a binary search tree In, we have implemented the transformation of ordered arrays into binary search trees. Therefore, here, we can first traverse the linked list, store the data of the nodes into an ordered array, and then convert the ordered array into a binary search tree.

class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        
        vector<int> nums;
        
        while (head != NULL)
        {
            nums.push_back(head->val);
            head = head->next;
        }
        
        return sortedArrayToBST(nums, 0, nums.size()-1);
    }
    
    TreeNode* sortedArrayToBST(vector<int>& nums, int begin, int end) {
        
        if (end < begin) return NULL; // Array is empty
        int mid = begin + (end - begin) / 2;
                
        TreeNode * tree = new TreeNode(nums[mid]); // Median as root
        tree->left = sortedArrayToBST(nums, begin, mid-1); // Left tree
        tree->right = sortedArrayToBST(nums, mid+1, end); // Right subtree
        
        return tree;
    }
};

2.2. Method 2

The core idea of transforming an ordered array into a binary search tree is to find the middle data of the array, take it as the root node, and then recursively build the left and right subtrees. Therefore, with the help of LeetCode 876 -- middle node of linked list We can quickly find the middle node of the list, and then set up the left and right subtrees with the two chains before and after the middle node.

As shown in the figure below, when the slow pointer points to the intermediate node, the last pointer points to the previous node of the intermediate node, and the slow - > next is the head node of the right sub chain. When the last - > next pointer points to NULL, the head node of the left sub chain is the head node.

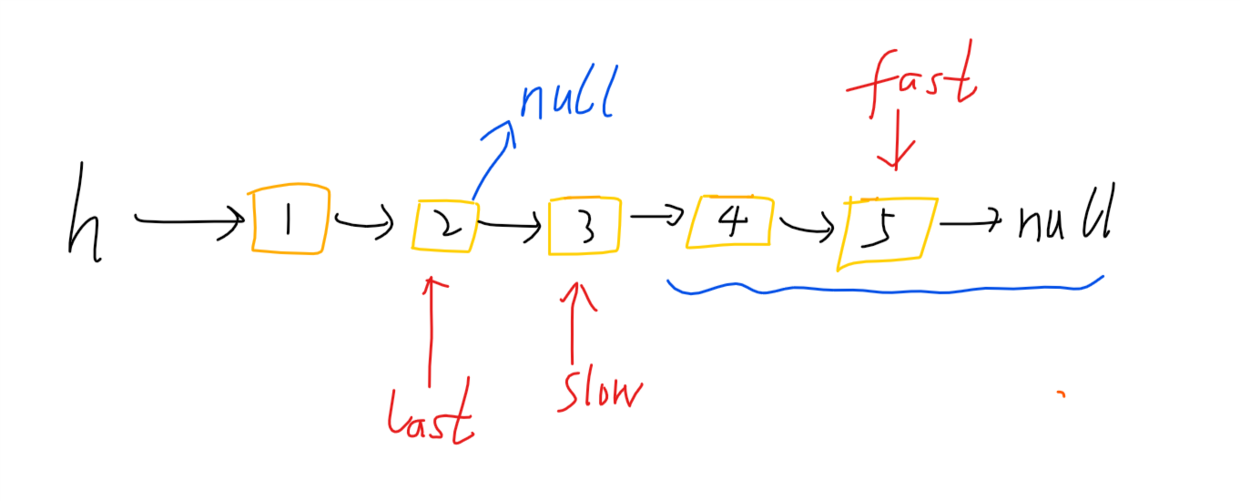
In addition, pay attention to a special case, when there is only one node, last, slow and fast all point to this node, then the left sub chain should be empty at this time.

class Solution {
public:
    TreeNode* sortedListToBST(ListNode* head) {
        
        ListNode* last = head;
        ListNode* slow = head;  
        ListNode* fast = head;  

        // Slow pointer to middle node at end of loop
        while(fast && fast->next)   
        {
            last = slow;
            slow = slow->next; 
            fast = fast->next->next;
        }
        
        if (slow == NULL) return NULL;
                
        TreeNode * tree = new TreeNode(slow->val); // Median as root
        
        if (last == slow) tree->left = NULL;
        else
        {         
            last->next = NULL;
            tree->left = sortedListToBST(head); // Left tree
        }
        tree->right = sortedListToBST(slow->next); // Right subtree
        
        return tree;
        
    }
    
};

For more highlights, please pay attention to "seniusen"!