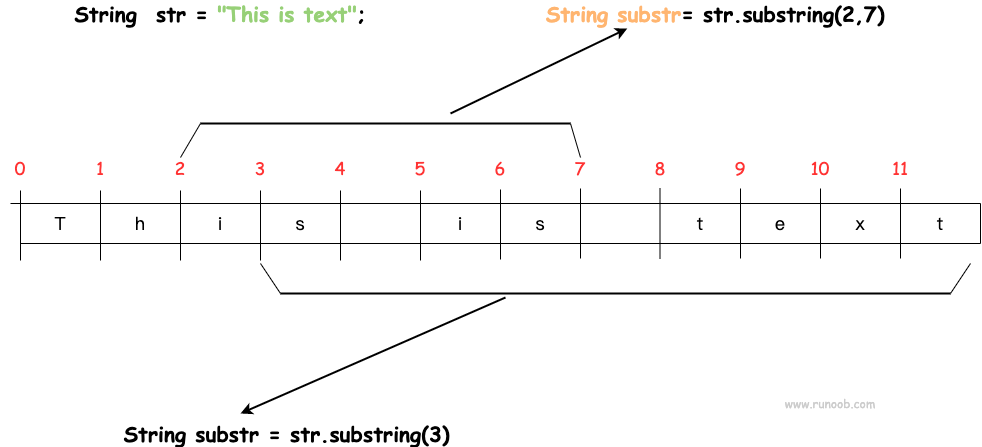
String (3)
Hello, everyone! I'm Xiao Sheng! I was busy learning java back-end technology, delayed the update of algorithm topics, and was ashamed to set up a weekly brushing plan to break through. Now I'm on the road of brushing again, keep it up! Go on!

String (3) Series of questions as follows
Subsequence (392)
392. Judgment Subsequence
Given the strings S and t, determine if s is a subsequence of T.
A subsequence of a string is a new string formed by the original string deleting (or not deleting) some characters without changing the relative position of the remaining characters. (For example, "ace" is a subsequence of "abcde" and "aec" is not).
Advanced:
If there are a lot of S inputs, called S1, S2,..., S K K >= 1 billion, you need to check if they are T in turn
Subsequence. In this case, how would you change the code?
Example 1:
Input: s = abc, t = ahbgdc output: true example 2:
Input: s = axc, t = ahbgdc Output: false
Tips:
0 <= s.length <= 100
0 <= t.length <= 10^4
Both strings consist of only lowercase characters.
MyCode
My idea is to solve this problem by moving the s subscript
First of all, to determine if s is a subsequence of t, I think every character in the s string must be used, so move by subscript and return true once all characters are satisfied to appear in t in order
Note that s,t is empty!!!
class Solution {
public boolean isSubsequence(String s, String t) {
int indexS = 0,n = s.length(), m = t.length();
if(n == 0) return true;
if(m == 0) return false;
for(int i=0;i<m;i++){
if(s.charAt(indexS) == t.charAt(i)){
indexS++;
}
if(indexS == n){
return true;
}
}
return false;
}
}
Execution time:1 ms, At all Java 85 Defeated in Submission.17%Users
Memory consumption: 36.2 MB, At all Java 77 defeated in submission.57%Users
Method 2: Dynamic Planning (Other's Code)
I think it's a bit cumbersome to use dynamic planning on official issues!
Let me start by describing the concept of dynamic planning
Dynamic programming essentially records the results that have been solved by developing a table of records, which can be directly accessed when the solution is needed again
Look in that record table to avoid recalculating subproblems to reduce time complexity. It's actually a space
Time-swapping algorithms. Dynamic programming can generally reduce exponential complexity to polynomial level.
Image description: Grab a dictionary to find words
Ideas:
1. Create a dictionary first (consider the solution dynamically based on t-length)
2. Use the dictionary to determine if there is a word.
3. Judgment: false / true
class Solution {
public boolean isSubsequence(String s, String t) {
int n = s.length(), m = t.length();
int[][] f = new int[m + 1][26];
for (int i = 0; i < 26; i++) {
f[m][i] = m;
}
for (int i = m - 1; i >= 0; i--) {
for (int j = 0; j < 26; j++) {
if (t.charAt(i) == j + 'a')
f[i][j] = i;
else
f[i][j] = f[i + 1][j];
}
}
int add = 0;
for (int i = 0; i < n; i++) {
if (f[add][s.charAt(i) - 'a'] == m) {
return false;
}
add = f[add][s.charAt(i) - 'a'] + 1;
}
return true;
}
}
High Precision Operations (66)
66.Add one
Given a non-negative integer represented by a non-empty array of integers, add one to it. The highest number is placed at the top of the array, and each element of the array stores only a single number.
You can assume that this integer does not start with zero except for the integer 0.
Example 1: Input: digits = [1,2,3] Output: [1,2,4] Interpretation: The input array represents the number 123.
Example 2: Input: digits = [4,3,2,1] Output: [4,3,2,2] Interpretation: The input array represents the number 4321.
Example 3: Input: digits = [0] Output: [1]
Tip: 1 <= digits.length <= 100 <= digits[i] <= 9
Method One On Stack and Out Stack (MyCode)
class Solution {
public int[] plusOne(int[] digits) {
int carry = 1;
Stack<Integer> stack = new Stack<Integer>();
for (int i = digits.length - 1; i >= 0 || carry != 0; i--) {
int sum = carry;
if (i >= 0) {
sum += digits[i];
}
stack.push(sum % 10);
carry = sum / 10;
}
int[] res = new int[stack.size()];
for (int i = 0; i < res.length; i++) {
res[i] = stack.pop();
}
return res;
}
}
Execution time:1 ms, At all Java Defeated 100 in submission.00%Users
Memory consumption: 37 MB, At all Java 20 beats in submission.84%Users
Method Two! (Other's Code)
The solution is absolute! That's wonderful! I can't describe it in any other words anymore.
class Solution {
public int[] plusOne(int[] digits) {
for (int i = digits.length - 1; i >= 0; i--) {
digits[i]++;
digits[i] = digits[i] % 10;
if (digits[i] != 0) return digits;
}
digits = new int[digits.length + 1]; // Classic
digits[0] = 1;
return digits;
}
}
String Transform (6)
6.Z-glyph transformation
Arranges a given string s in Z-shape from top to bottom, left to right, based on a given number of rows, numRows.
For example, if the input string is "PAYPALISHIRING" and the number of lines is 3, the arrangement is as follows:
P A H N
A P L S I I G
Y I R
After that, your output needs to be read line by line from left to right to produce a new string, such as "PAHNAPLSIIGYIR".
Please implement this function that transforms a string to a specified number of lines:
string convert(string s, int numRows);
Example 1:
Input: s = PAYPALISHIRING, numRows = 3
Output: "PAHNAPLSIIGYIR"
Example 2:
Input: s = PAYPALISHIRING, numRows = 4
Output: "PINALSIGYAHRPI"
Explanation:
P I N
A L S I G
Y A H R
P I
Example 3:
Input: s = A, numRows = 1 Output:'A'
Tips:
1 <= s.length <= 1000
s consists of English letters (lower and upper case),',', and'.
1 <= numRows <= 1000
Method One Traversal (MyCode)
Here are my ideas for solving problems:

class Solution {
public String convert(String s, int numRows) {
String[] string = new String[numRows];
Boolean flag = true; // true down false up
int count = 0;
String sum = "";
for(int i=0;i<numRows;i++){
if(string[i]==null){
string[i]="";
}
}
if(numRows == 1){
return s;
}
for(int i=0;i<s.length();i++){
// Judging direction and number of rows
if(flag == true && count<=numRows-1){ // Decide to run numRows-1 down
count++;
}else if(flag == true && count>numRows-1){
count--;
flag = false;
}else if(flag == false && count>1){ //Judge to run numRows-1 up
count--;
}else if(flag == false && count==1){
count++;
flag = true;
}
string[count-1] += s.charAt(i);
}
for(int i=0;i<numRows;i++){
sum += string[i];
}
return sum;
}
}
Execution time:14 ms, At all Java 22 beats in submission.71%Users
Memory consumption: 39.3 MB, At all Java 15 beats in submission.16%Users
String Matching (459)
459.Duplicate substring
Given a non-empty string, determine if it can be repeated multiple times by one of its substrings. The given string contains only lowercase English letters and is not longer than 10000.
Example 1:
Input:'abab'
Output: True
Interpretation: The substring "ab" can be repeated twice.
Example 2:
Input:'aba'
Output: False
Example 3:
Input:'abcabcabcabc'
Output: True
Interpretation: The substring "abc" can be repeated four times. (Or the substring "abc abc" can be repeated two times.)
Method One Segment Comparison
Solving ideas:
First I use depart to determine the number of segments, countflag to determine if each segment is the same
I want the maximum number of segments of string length n while (depart<=n)
class Solution {
public boolean repeatedSubstringPattern(String s) {
int n = s.length();
int depart = 2; // Divide into portions
int countflag = 0; // Judgement Marker
while(depart<=n){
if(n%depart == 0){
for(int i=0;i<=n-n*2/depart;i+=n/depart){
if(s.substring(i,i+n/depart).equals(s.substring(i+n/depart,i+n*2/depart))){
countflag++;
}
}
if(countflag == depart-1){
return true;
}
}
countflag = 0;
depart++;
}
return false;
}
}
Execution time:34 ms, At all Java 45 defeated in submission.58%Users
Memory consumption: 38.6 MB, At all Java 92 defeated in submission.36%Users
Method 2: String Matching (Other's Code)
Absolutely! That's too strong! Nothing to say, thorough!
// int indexOf(int ch, int fromIndex)
// Returns the index at the first occurrence of the specified character in this string, starting with the specified index.
class Solution {
public boolean repeatedSubstringPattern(String s) {
return (s + s).indexOf(s, 1) != s.length();
}
}
Center Expansion Method (5)
5.Longest Palindromic Substring
Give you a string s, find the longest palindrome substring in S.
Example 1:
Input: s = "babad"
Output:'bab'
Explanation: "aba" is also the answer to the question.
Example 2:
Input: s = cbbd
Output:'bb'
Example 3:
Input: s = "a" output: "a" Example 4:
Input: s = "ac" output: "a"
Tips:
1 <= s.length <= 1000
s consists only of numbers and English letters (uppercase and/or lowercase)
Method One Violent Solution (MyCode)
First, I want to write a function to determine palindrome
Then I try to use a double loop to start with the longest palindrome string
Returns the character whenever a judgment is a palindrome function and continues the query instead
The first character of the string, s.substring(0,1), is returned at the end without a solution.
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
for(int i=n;i>=2;i--){
for(int j=0;j+i<=n;j+=1){
if(palindrome(s.substring(j,j+i))){
return s.substring(j,j+i);
}
}
}
return s.substring(0,1);
}
public boolean palindrome(String s){ // Judging palindrome function
int i=0,j=s.length()-1;
while(i<j){
if(s.charAt(i) == s.charAt(j)){
i++;
j--;
}else{
return false;
}
}
return true;
}
}
Method 2: Dynamic planning
Boundary conditions for dynamic programming:
For a substring, if it is a palindrome string and is longer than 2, it will still be a palindrome string after removing the first and last two letters of it. For example, for a string} "bab" is a palindrome string, then "a bab a" must be a palindrome string because both the first and last letters are "a".
Based on this idea, we can solve this problem by dynamic programming. We use P(i,j)P(i,j) to indicate whether the string composed of the I I to j j letters of the string s s (which i s represented below as s[i:j]s[i:j]) i s a palindrome string:
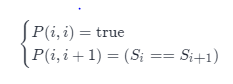
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] indicates whether s[i..j] i s a palindrome string
boolean[][] dp = new boolean[len][len];
// Initialization: All substrings of length 1 are palindromes
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
// Recursive Start
// Enumerate Substring Length First
for (int L = 2; L <= len; L++) {
// Enumerate the left boundary, the upper limit of the left boundary can be set looser
for (int i = 0; i < len; i++) {
// The right boundary can be determined by L and i, that is, j - i + 1 = L
int j = L + i - 1;
// If the right boundary crosses, you can exit the current loop
if (j >= len) {
break;
}
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// As long as dp[i][L] == true i s true, the substring s[i..L] i s palindrome, and the palindrome length and starting position are recorded.
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}