Topic Description
Given a string s, find the longest palindrome substring in S. You can assume that the maximum length of S is 1000.
Example 1:
- Input: "babad"
- Output: "bab"
Note that "aba" is also an effective answer.
Example 2:
- Input: "cbbd"
- Output: "bb"
Thoughts on Problem Solving
1. Violent resolution
The easiest thing to think of is the violent solution. Find out each substring of the original string s, and then judge whether it is palindrome or not, and find the longest one.
class Solution { //Determine whether a string is palindrome public static boolean judge(String s){ StringBuffer sb = new StringBuffer(s); sb.reverse(); String str = new String(sb); if(s.equals(str)){ return true; } return false; } public String longestPalindrome(String s){ int l = s.length(); //If the length of a string is less than 2, the string is returned. if(l < 2){ return s; } //Get each substring through two for loops and decide whether it is palindrome or not //Here, from the longest substring to the shortest substring, so when the first substring is palindrome, it is the longest palindrome substring. for(int i = l; i > 0; i--){ for(int j = 0; j <= l - i; j++){ String str = s.substring(j, j + i); if(judge(str)){ return str; } } } return s; } }
The time complexity of each substring is O(N2)O(N^2)O(N2), and the time complexity of judging whether the substring is palindrome is O(N)O(N)O(N), so the time complexity of violent solution is O(N3)O(N^3)O(N3). The complexity of this algorithm is too high to satisfy the interviewer.
2. Dynamic programming
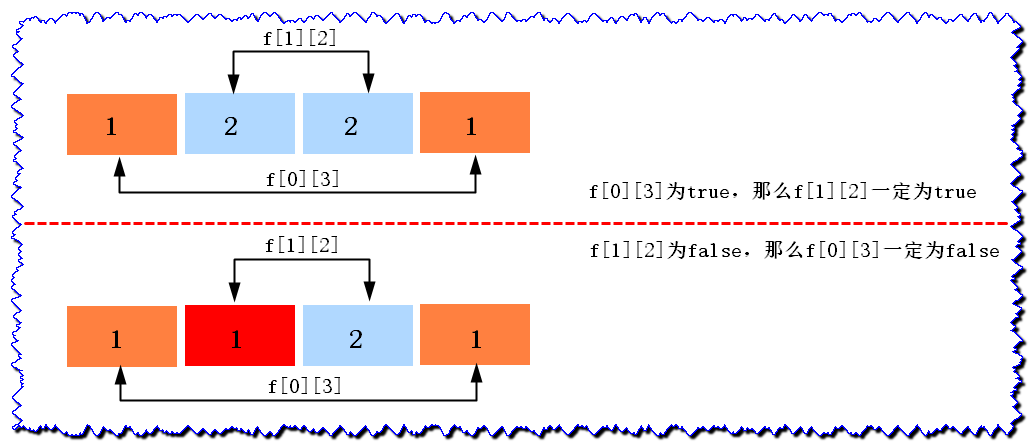
_For string SSS, suppose that f [i] [j] f [i] [j] f [i] [i] [j] f [i] [j] indicates whether the substring of string SSS subscripts from iii to jjj is a palindrome substring.
- I f f [i] [j] f [i] [j] f [i] [i] [j] f [i] [j] is palindrome, then f[i+1][j_1]f[i+1][j-1]f[i+1][j_1] must be palindrome substring
- I f f[i+1][j 1]f[i+1][j-1]f[i+1][j 1] is not palindrome, then f[i][j]f[i][j]f[i][j] f [i] [j] must not be palindrome substring
The longest palindrome substring can be decomposed into a series of sub-problems, which can be solved by dynamic programming. From this we can get the recursive equation of dynamic programming:
f[i][j]={f[i+1][j_1],S[i]=S[j]false,S[i] is not equal to S [j] f [i] [j]= begin {cases}. f[i+1][j-1] &,S[i]=S[j] \\ False & amp;, S [i] is not equal to S[j].\ \ end{cases}f[i][j]={f[i+1][j_1]false, S[i]=S[j],S[i] is not equal to S[j]
Initial state
{f[i][i]=truef[i][i+1]=true if S[i]==S[i+1]\begin{cases} f[i][i]=true \\ f[i][i+1]=true \ if \ S[i]==S[i+1]\\ \end{cases}{f[i][i]=truef[i][i+1]=true if S[i]==S[i+1]
- F [i] [i] = truef [i] [i] = truef [i] [i] = truef [i] [i] = true denotes a single character as a palindrome
- f[i][i+1]=true if S[i]==S[i+1] f[i][i+1]=true if\ S [i]= S [i + 1]= true [i + 1] f[i][i+1]=true if S [i]= S [i + 1] means that two connected characters are palindromes
C++ code:
class Solution { public: string longestPalindrome(string s) { //If the string is empty, return empty if (s.empty()) return ""; //String length int len = s.size(); //Single character if (len == 1) return s; //Keep the longest palindrome substring length int longest = 1; //Keep the Starting Point of the Longest Palindrome Substring int start=0; //A vector container is defined with the element type vector < int > initialized to contain len vector < int > objects. //Each object is a copy of a newly created vector < int > object, and the newly created vector < int > object is initialized to contain len 0. //Similar to creating a two-dimensional array of lenxlen, elements can be accessed by dp[i][j]. vector<vector<int>> dp(len,vector<int>(len)); //initial condition for (int i = 0; i < len; i++) { //Two-dimensional array diagonals are single characters, all of which are 1 dp[i][i] = 1; if(i<len-1) { if (s[i] == s[i + 1])//Two contiguous characters are identical { dp[i][i + 1] = 1;//Palindrome, marked 1 start=i;//Change the starting position longest=2;//The longest palindrome substring length is 2 } } } //String Length >= 3 for (int l = 3; l <= len; l++)//Traversing the length of each seed string { for (int i = 0; i+l-1 < len; i++)//Enumeration of the Starting Point of Substring { int j=l+i-1;//End if (s[i] == s[j] && dp[i+1][j-1]==1) //If the characters at both ends of the substring are the same and the substrings that remove the characters at both ends are palindrome substrings { dp[i][j] = 1;//At this point, the substring is palindrome, marked 1 start=i;//Update Start Location longest = l;//Update Maximum Length } } } return s.substr(start,longest);//start starts in the interception string and intercepts longest characters } };
Java code:
class Solution { public String longestPalindrome(String s) { if("".equals(s)){ return ""; } int len = s.length(); if(len == 1){ return s; } int sLength = 1; int start = 0; int[][] dp = new int[len][len]; for(int i = 0; i < len; i++){ dp[i][i] = 1; if(i < len - 1 && s.charAt(i) == s.charAt(i+1)){ dp[i][i+1] = 1; sLength = 2; start = i; } } for(int l = 3; l <= len; l++){ for(int i = 0; i + l -1 < len; i++){ int j = i + l - 1; if(s.charAt(i) == s.charAt(j) && dp[i+1][j-1] == 1){ dp[i][j] = 1; start = i; sLength = l; } } } return s.substring(start,start+sLength); } }
Python 3 code:
class Solution: def longestPalindrome(self, s: str) -> str: length = len(s) # Calculate string length if length == 0: return "" if length == 1: return s sLength = 1 start = 0 dp = [[0 for i in range(length)] for j in range(length)] # Create a two-dimensional array initialized to 0 for i in range(0, length): dp[i][i] = 1 if i < length - 1 and s[i] == s[i+1]: dp[i][i+1] = 1 sLength = 2 start = i for l in range(3, length+1): for i in range(0, length-l+1): j = i + l - 1 if s[i] == s[j] and dp[i+1][j-1] == 1: dp[i][j] = 1 start = i sLength = l return s[start : start+sLength]
3. Central Expansion Method
The idea of_central expansion is that when traversing to an element of an array, it expands to both sides with this element as the center, and if the elements on both sides are the same, it continues to expand, otherwise it stops expanding. The complexity of the algorithm is O(N2)O(N^2)O(N2).
The following figure: When traversing to 3:00
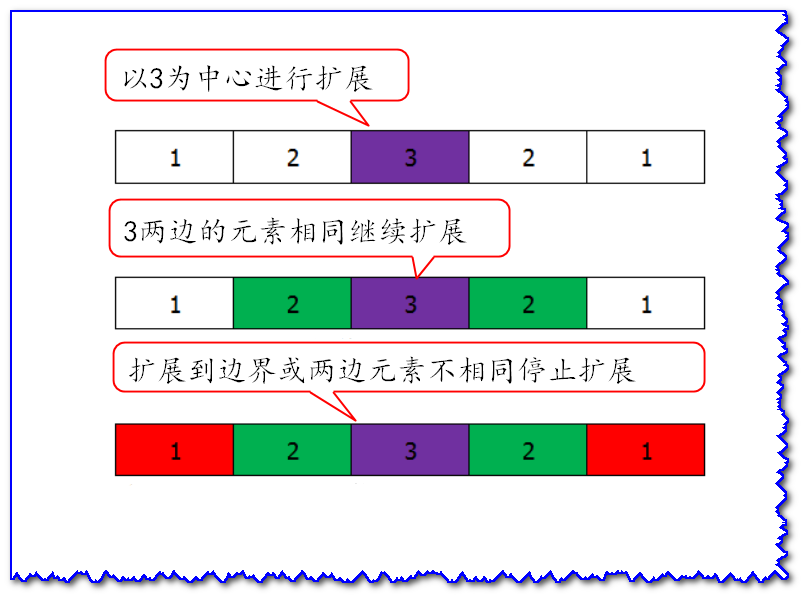
However, single character expansion is flawed when the length of the string is even, such as 1221.
1, 2, 2, 1 is a palindrome string, but no symmetric center can be found, which makes it difficult to extend from one element to both sides.
- 1. Expanding around a single character and two adjacent characters respectively (the following code uses this method)
- 2. Fill in 1, 2, 2, 1. For example, fill in with # to get:, 1,, 2,, 2,, 1,#
Java code:
class Solution { public String longestPalindrome(String s) { if(s == null || s.length() < 1) return ""; int start = 0; int end = 0; //The central expansion method traverses the central points in turn for(int i = 0; i < s.length(); i++){ //Finding the Length of Expansion Center int len1 = expandLen(s, i, i); //Centering on each character int len2 = expandLen(s, i, i+1); //With each adjacent two characters as the center int len = Math.max(len1, len2); if(len > end - start){ start = i - (len - 1) / 2; end = i + len / 2; } } return s.substring(start, end+1); } public int expandLen(String s, int L, int R){ int left = L; int right = R; while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){ left--; right++; } return right - left - 1; } }

C++ code:
class Solution { public: string longestPalindrome(string s) { int len=s.size(); if(len==0||len==1) return s; int start=0;//Record the starting position of palindrome substring int end=0;//Record palindrome substring termination position int mlen=0;//Recording the Length of the Maximum Palindrome Substring for(int i=0;i<len;i++) { int len1=expendaroundcenter(s,i,i); int len2=expendaroundcenter(s,i,i+1); mlen=max(max(len1,len2),mlen); if(mlen>end-start+1) { start=i-(mlen-1)/2; end=i+mlen/2; } } return s.substr(start,mlen); //This function means to get a string of mlen length from start } private: int expendaroundcenter(string s,int left,int right) //Calculating the length of palindrome string centered on left and right { int L=left; int R=right; while(L>=0 && R<s.length() && s[R]==s[L]) { L--; R++; } return R-L-1; } };
Python 3 code:
class Solution: def longestPalindrome(self, s: str) -> str: def expand(s, left, right): while left >= 0 and right < len(s) and s[left] == s[right]: left -= 1 right += 1 return right - left - 1 start = 0 end = 0 for i in range(len(s)): len1 = expand(s, i, i) len2 = expand(s, i, i+1) max_len = max(len1, len2) if max_len > end - start: start = i - int((max_len-1)/2) end = i + int(max_len/2) return s[start : end+1]
Manacher algorithm
Direct examples are given to illustrate:
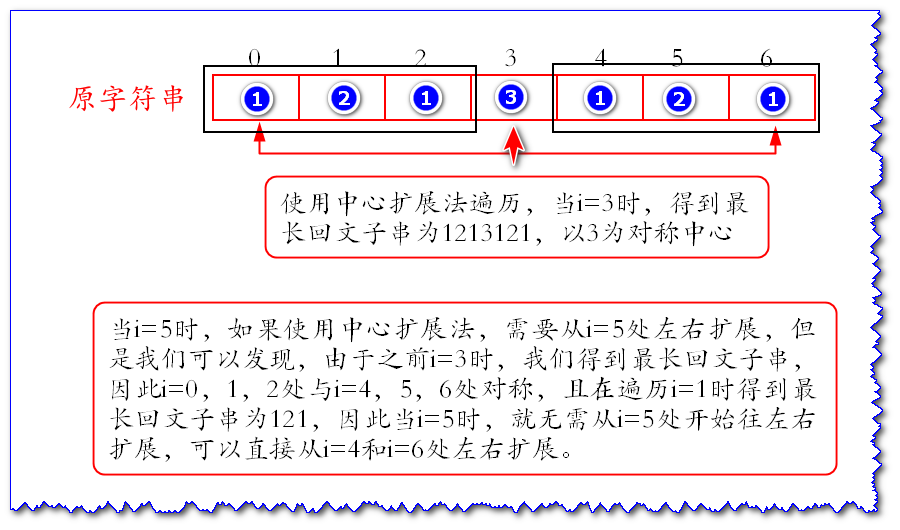
The core idea of Manacher algorithm is to use palindrome substrings generated during previous traversals.
1. Principle
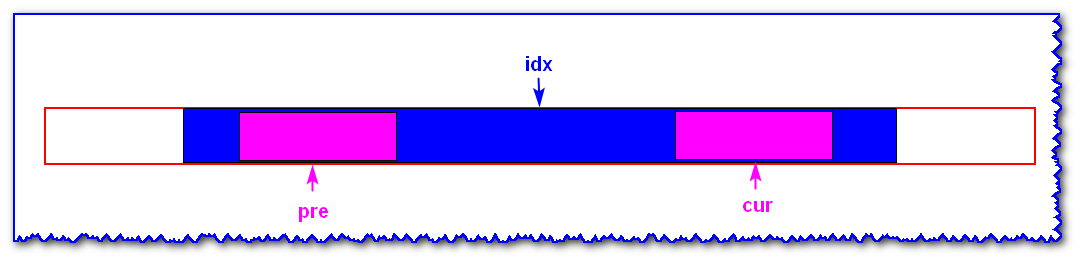
As shown above:
- idxidxidx represents the symmetric axis of the blue palindrome substring (known)
- Now find the palindrome substring with curcurcur as the symmetric axis (unknown)
- Preprepreprep is the symmetric axis with idxidx and the symmetric position of curcurcur (traversal to curcurcur, prepreprepreprep is known)
Scenario 1: The palindrome substrings of I'I ' i'exceed the left boundary of the palindrome substrings of idxidxidx
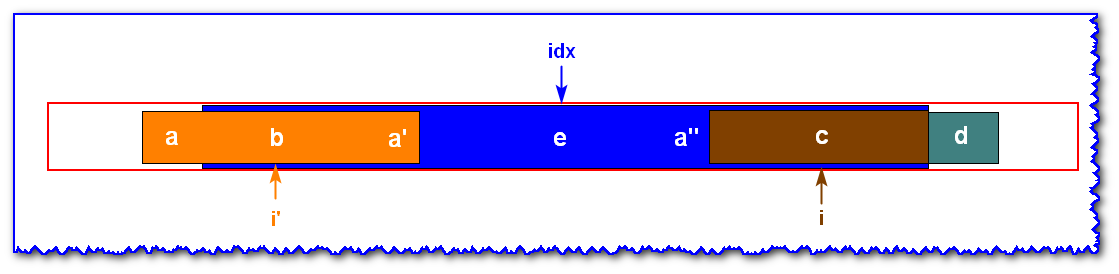
Given that idxidxidx is the central axis of the blue block substring, we now seek the palindrome substring with i as the central axis.
- I I I is in the palindrome substring with idxidx as its central axis, I'I & X 27; i'is iii's symmetric point about idxidx, and the palindrome substring with I'I & X 27; i'as its central axis is known (orange block).
- Where I I I points to ccc, I'I & x 27; i'points to bbb, idxidxidx points to eee (lowercase characters are variables, capital letters are specific characters)
- So from the eee-centered palindrome substring, we know that b=cb=cb=c
- Because the palindromes of idxidxidx do not include a a A and D D d, a! = da! = da! = D (when a=da=da=d, the palindrome substrings of idxidx will be extended)
- Because IDX IDX IDX left to bbb and idxidx right to c c c are equal, and a!=da!=da!=d, the palindrome radius centered on ccc is only IDX right location(c)idx right-location(c)idx right location(c).
- If a a a's symmetry point about bbb-centered palindromes is a'a & # x27; a'. The symmetry point of a'a & # x27; A'palindrome centered on eee is a''a & # x27; & # x27; & # x27; a', then a=a'= a'= a'!= Da = A & # x27; = A & # x27; & # x27; = Da = a'= a'!= d
Examples are given to illustrate:
Because there are even and odd string lengths, we use # to fill in, as follows:___________.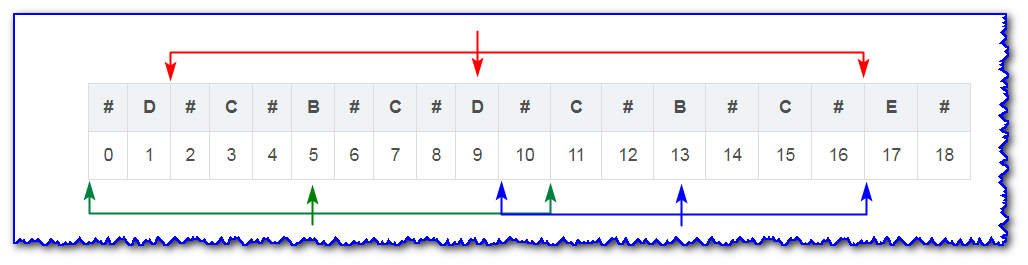
- When traversing to 13B, the palindrome substrings with 9D as the central axis are from 2 to 16 (as previously traversed, known), and the length is 16_2+1=1516-2+1=1516_2+1=1516_2+1=15.
- The palindrome substring centered on No. 5 B is from No. 0 to No. 10 (known), and its length is 10_0+1=1110-0+1=1110_0+1=11.
- The symmetric point of No. 13 B about No. 9D is No. 5 B, and now the palindrome substring with No. 13 B as the symmetric axis is required.
No. 1 D and No. 17E are not equal. Now, as long as the disc decides whether the palindrome substring centered on No. 13 B contains No. 17 or not.
- If 17 E is included, then its point of symmetry for 13 B is 9D, and the point of symmetry for 9D for 5 B is 1D.
- According to the symmetry, No. 17 E should be equal to No. 9 D and No. 1 D, which is obviously different.
Therefore, the palindrome substrings with No. 13 B as the central axis do not include No. 17 E. According to the palindrome substrings with No. 5 B and No. 9 D as the central axis, we can see that:
- No. 2 # to No. 5 B equals No. 8 # to No. 5 B
- No. 10 to No. 13B equals No. 16 to No. 13B
Case 2: The palindrome substring idxidxidx of I'I & x 27; i'contains the palindrome substring
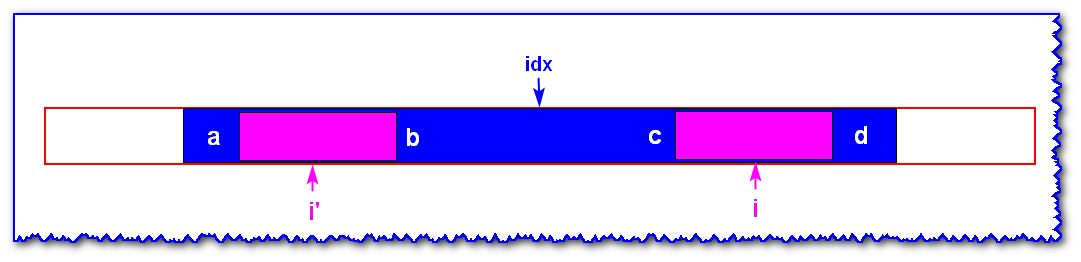
The largest palindrome substring of known I I i's symmetric point I'I & x 27; i's on idxidx's central axis is shown in the figure above.
- Because the palindrome substrings of I'I & x 27; i'do not include a,ba,ba,b, then a!=ba!=ba!=b
- And because a,da,da,d and b,cb,cb,c are symmetric about idxidx, remember b=c,a=db=c,a=db=c,a=d, so c!=dc!=dc!=d
- Because the character between ccc and ddd is palindrome, because the character between ccc and ddd is symmetrical between aaa and bbb of idxidx, and between aaa and bbb is palindrome string, so the character between ccc and ddd is palindrome string. So the length of the palindrome substring of i I i is the same as that of i'I & X 27; i'
Examples are given to illustrate: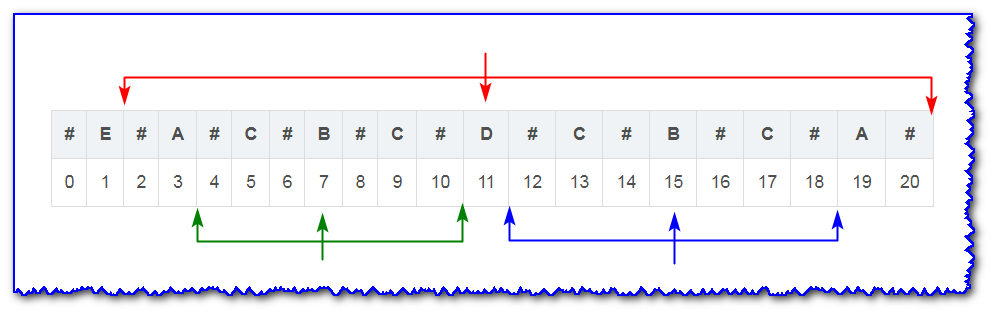
Case 3: The left boundary of the palindrome substring of I'I & x 27; i'coincides with the left boundary of the palindrome substring of idxidx
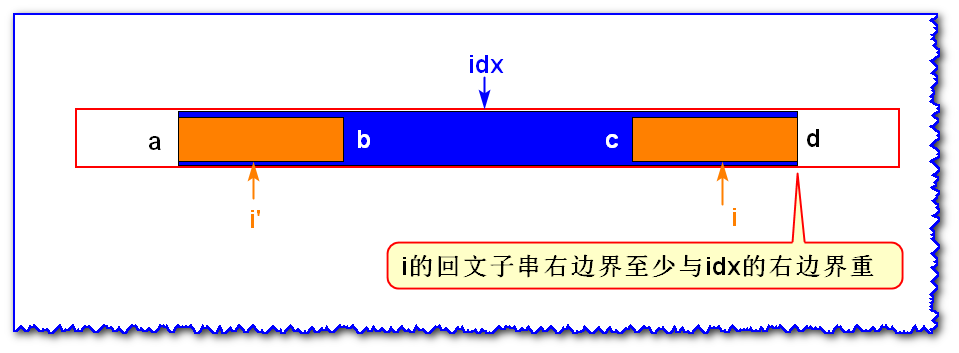
From the palindrome substring centered on idxidx, it can be seen that b=c,a!=db=c,a!=db=c,a!=d, and the palindrome length of I'I & # x 27; i'is between aaa and bbb (excluding a,ba,ba,b).
So the length of the palindrome substring of iii is at least as shown in the figure above.
- If c=dc=dc=d, the palindrome about iii as the central axis can be extended
- If c!=dc!=dc!=d, it happens to be shown in the figure above.
Examples (c=d):
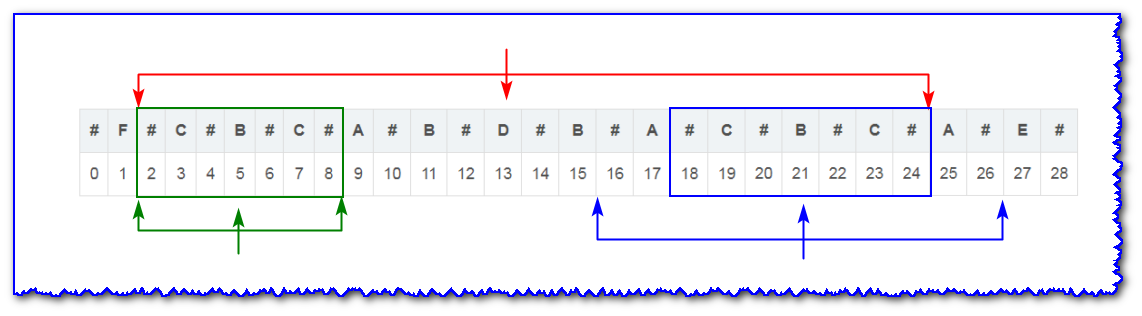
I I i's longest palindrome substring of I'I & X 27; i's symmetry point about idxidx is shown above, and the left boundary of I'I & X 27; i's palindrome coincides with idxidxidx, so iii-centered palindromes need to be expanded from the blue box boundary to the left and right sides.
Case 4: I'I & x27; i's palindrome substring is not included in idxidxidx's palindrome substring
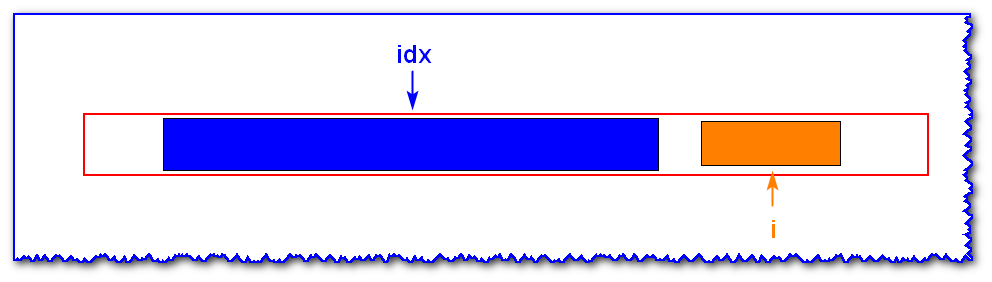
At this point, we do not have any information to use, can only take iii as the central axis, extending to the left and right sides. Find out its longest palindrome substring.
2. C++ Code
class Solution { public: string longestPalindrome(string s) { //Calculate string length int n = s.size(); if(n <= 1) return s; //Generate a string str containing 2*n+1 character 0 string str(2*n+1,'0'); bool flag = 1; int j = 0; int maxIdx = 0; //Fill in the character and get a string like # 1 # 2 # 3 # 2 # 1. for(int i=0; i<2*n+1; i++){ if(flag){ str[i]='#'; flag = false; }else{ str[i] = s[j++]; flag = true; } } //Represents the radius of palindrome substrings with i as the central axis and does not contain the symmetric axis //For example, abcdcba, the subscript of d is 4, radius[4] = 3, radius[0] = 0 vector<int> radius(2*n+1,0); int idx = 0; //A central axis subscript representing the last palindrome substring int rad = 1; //idx can contain the next character subscript in the largest range for(int i=1; i<2*n+1; i++){ //Situation IV if(i >= rad){ forceExtend(str, radius, idx, rad, i); maxIdx = (radius[i] > radius[maxIdx] ? i : maxIdx); }else if(i < rad){ int j = 2*idx - i; //i On the Symmetric Point j of idx int idx_radius = idx - radius[idx]; //Left boundary subscripts of idx palindrome substrings int j_radius = j - radius[j];//The left boundary subscript of the palindrome substring of j if(j_radius > idx_radius){ //Situation II radius[i] = radius[j]; //i's palindrome substring is the same length as its palindrome substring about idx symmetry points }else if(j_radius < idx_radius){//Situation I radius[i] = idx + radius[idx] - i;//Right boundary subscript-i subscript of idx }else{ //Situation III radius[i] = idx + radius[idx] - i;//at least int count = 1; //When equal, continue to expand while((i + radius[i] + count) <= str.size() && (i - radius[i] - count) >= 0 && str[i + radius[i] + count] == str[i - radius[i] - count]){ count++; } //Unequal time radius[i] += (count - 1); //Update the next character subscript at the center and right boundary of the longest palindrome substring if(i + radius[i] >= rad){ idx = i; rad = i + count; } } //Update the center of the longest palindrome substring maxIdx = (radius[i] > radius[maxIdx] ? i : maxIdx); } } string ret = getMaxSubString(str, maxIdx, radius[maxIdx]); return ret; } //Situation IV void forceExtend(const string& str, vector<int>& radius, int &idx, int &rad, const int k){ int count = 1; while((k - count) >=0 && (k + count) < str.size() && str[k - count] == str[k + count]){ count++; } radius[k] = count - 1; if((k + radius[k]) >= rad){ idx = k; rad = k + count; } } //Find the longest palindrome substring string getMaxSubString(const string &str,const int k,const int r){ string ret(r, '0'); int j = 0; for(int i = k-r+1; i <= k+r; i+=2){ ret[j++] = str[i]; } return ret; } };
3. Java code
public class Solution { public static String longestPalindrome(String s) { int n = s.length(); if (n <= 1) return s ; StringBuilder strb = new StringBuilder(); strb.append("#"); for (int i = 0; i < s.length(); i++) { strb.append(s.charAt(i)); strb.append("#"); } int len = strb.length(); int[] radius = new int[len]; int idx = 0; //A central axis subscript representing the last palindrome substring int rad = 1; //idx can contain the next character subscript in the largest range int j = 0; int maxIdx = 0; for (int i = 1; i < len; i++) { //Situation IV if(i >= rad){ int count = 1; while((i - count) >=0 && (i + count) < strb.length() && strb.charAt(i - count) == strb.charAt(i + count)){ count++; } radius[i] = count - 1; if((i + radius[i]) >= rad){ idx = i; rad = i + count; } maxIdx = (radius[i] > radius[maxIdx] ? i : maxIdx); }else if(i < rad){ j = 2*idx - i; //i On the Symmetric Point j of idx int idx_radius = idx - radius[idx]; //Left boundary subscripts of idx palindrome substrings int j_radius = j - radius[j];//The left boundary subscript of the palindrome substring of j if(j_radius > idx_radius){ //Situation II radius[i] = radius[j]; //i's palindrome substring is the same length as its palindrome substring about idx symmetry points }else if(j_radius < idx_radius){//Situation I radius[i] = idx + radius[idx] - i;//Right boundary subscript-i subscript of idx }else{ //Situation III radius[i] = idx + radius[idx] - i;//at least int count2 = 1; //When equal, continue to expand while((i + radius[i] + count2) < len && (i - radius[i] - count2) >= 0 && strb.charAt(i + radius[i] + count2) == strb.charAt(i - radius[i] - count2)){ count2++; } //Unequal time radius[i] += (count2 - 1); //Update the next character subscript at the center and right boundary of the longest palindrome substring if(i + radius[i] >= rad){ idx = i; rad = i + count2; } } //Update the center of the longest palindrome substring maxIdx = (radius[i] > radius[maxIdx] ? i : maxIdx); } } StringBuilder ret = new StringBuilder(); for(int i = maxIdx-radius[maxIdx]+1; i <= maxIdx + radius[maxIdx]; i+=2){ ret.append(strb.charAt(i)); } return ret.toString(); } }
4. Python 3 Code
class Solution: def longestPalindrome(self, s: str) -> str: n = len(s) if n <= 1: return s st = '#' + '#'.join(s) + '#' sLen = len(st) radius = [0] * sLen idx = 0 rad = 1 maxIdx = 0 for i in range(1, sLen): if i >= rad: count = 1 while (i - count) >= 0 and (i + count) < sLen and st[i - count] == st[i + count]: count += 1 radius[i] = count - 1 if (i + radius[i]) >= rad: idx = i rad = i + count maxIdx = i if (radius[i] > radius[maxIdx]) else maxIdx elif i < rad: j = 2 * idx - i idx_radius = idx - radius[idx] j_radius = j - radius[j] if j_radius > idx_radius: radius[i] = radius[j] elif j_radius < idx_radius: radius[i] = idx + radius[idx] - i else: radius[i] = idx + radius[idx] - i count2 = 1 while (i + radius[i] + count2) < sLen and (i - radius[i] - count2) >= 0 and st[i + radius[i] + count2] == st[i - radius[i] - count2]: count2 += 1 radius[i] += (count2 - 1) if (i + radius[i]) >= rad: idx = i rad = i + count2 maxIdx = i if (radius[i] > radius[maxIdx]) else maxIdx ret = [] for i in range(maxIdx-radius[maxIdx]+1, maxIdx + radius[maxIdx]+1, 2): ret.append(st[i]) return ''.join(ret)