AcWing 2. 01 knapsack problem
State representation
f ( i , j ) f(i, j) f(i,j) represents the optimal solution of the first i articles in the case of volume j
State calculation
- f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i − 1 , j − v ( i ) ) + w ( i ) ) f(i , j) = max(f(i - 1, j), f(i - 1, j - v(i)) + w(i)) f(i,j)=max(f(i−1,j),f(i−1,j−v(i))+w(i))
- f ( i − 1 , j ) f(i - 1, j) f(i − 1,j) indicates the maximum value of the i-th item
-
f
(
i
−
1
,
j
−
v
(
i
)
)
+
w
(
i
)
f(i - 1, j - v(i)) + w(i)
f(i − 1,j − v(i))+w(i) indicates that the maximum value of the ith item is selected, and the ith item accounts for
v
(
i
)
v(i)
The space of v(i) has a value of
w
(
i
)
w(i)
w(i)
Optimization:
State representation
f
(
j
)
f(j)
f(j) represents the optimal solution under capacity j
b
a
c
k
u
p
(
i
)
backup(i)
The backup(i) array will the current before the next iteration
f
(
i
)
f(i)
f(i) back up the array
State calculation
Each time you calculate the status of the next round, you need to use the updated results of the previous round of iteration. Backing up the iteration results of the previous round with a new array can make the next round of calculation not affected by your own calculation results
Positive sequence calculation:
f
(
j
)
=
m
a
x
(
f
(
j
)
,
b
a
c
k
u
p
(
j
−
v
(
i
)
)
+
w
(
i
)
)
f(j) = max(f(j), backup(j - v(i)) + w(i))
f(j)=max(f(j),backup(j − v(i))+w(i)), where j increases from 0 to the maximum capacity of the backpack
More succinctly, reverse order iteration is used for calculation, and there is no need to use another array to back up the status of the previous round:
f
(
j
)
=
m
a
x
(
f
(
j
)
,
f
(
j
−
v
(
i
)
)
+
w
(
i
)
)
f(j) = max(f(j), f(j - v(i)) + w(i))
f(j)=max(f(j),f(j − v(i))+w(i)), where
j
from
Back
package
most
large
Allow
amount
Deliver
reduce
reach
v
(
i
)
j decreases from the maximum capacity of the backpack to v(i)
j decreases from the maximum capacity of the backpack to v(i)
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = m; j >= v[i]; j --)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
/*
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
*/
AcWing 3. Complete knapsack problem
State representation
f ( i , j ) f(i, j) f(i,j) represents the optimal solution of the first i items under the condition of capacity j
State calculation
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
−
k
∗
v
)
+
k
∗
w
)
,
k
=
0
,
1
,
2...
(
j
>
=
k
∗
v
)
f(i, j) = max(f(i - 1, j - k * v) + k * w), k = 0, 1, 2 ...(j >= k * v)
f(i,j)=max(f(i−1,j−k∗v)+k∗w),k=0,1,2...(j>=k∗v)
Equivalent deformation
- f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i − 1 , j − v ) + w , f ( i − 1 , j − 2 ∗ v ) + 2 ∗ w , f ( i − 1 , j − 3 ∗ v ) + 3 ∗ w , . . . ) f(i,j) = max(f(i - 1, j), f(i - 1, j - v) + w, f(i - 1, j - 2 * v) + 2 * w, f(i - 1, j - 3 * v) + 3 * w, ...) f(i,j)=max(f(i−1,j),f(i−1,j−v)+w,f(i−1,j−2∗v)+2∗w,f(i−1,j−3∗v)+3∗w,...)
-
f
(
i
,
j
−
v
)
=
m
a
x
(
f
(
i
−
1
,
j
−
v
)
,
f
(
i
−
1
,
j
−
2
∗
v
)
+
w
,
f
(
i
−
1
,
j
−
3
∗
v
)
+
2
∗
w
,
.
.
.
)
f(i,j - v) = max(~~~~~~~~~~~~ f(i - 1, j - v) ~~~~~~~~, f(i - 1, j - 2 * v) + ~~~~~~ w, f(i - 1, j - 3 * v) + 2 * w, ...)
f(i,j−v)=max( f(i−1,j−v) ,f(i−1,j−2∗v)+ w,f(i−1,j−3∗v)+2∗w,...)
Get:
f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i , j − v i ) + w i ) f(i, j) = max(f(i - 1, j), f(i, j - vi) + wi) f(i,j)=max(f(i−1,j),f(i,j−vi)+wi)
optimization
f ( j ) = m a x ( f ( j ) , f ( j − v i ) + w i ) f(j) = max(f(j), f(j - vi)+ wi) f(j)=max(f(j),f(j−vi)+wi)
//Final edition
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++ )
for(int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
//Optimized version
/*
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
{
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
*/
//Simple method
/*
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
for(int k = 0; k * v[i] <= j; k ++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}
*/
AcWing 4. Multiple knapsack problem
State calculation
f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i − 1 , j − k ∗ v ) + k ∗ w ) f(i, j) = max(f(i - 1, j), f(i - 1, j - k * v) + k * w) f(i,j)=max(f(i−1,j),f(i−1,j−k∗v)+k∗w)
optimization
f
(
j
)
=
m
a
x
(
f
(
j
)
,
f
(
j
−
k
∗
v
)
+
k
∗
w
)
f(j) = max(f(j), f(j - k * v) + k * w)
f(j)=max(f(j),f(j−k∗v)+k∗w)
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int n, m;
int f[N];
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
{
int v, w, s;
cin >> v >> w >> s;
for(int j = m; j >= 0; j -- )
for(int k = 1; k <= s && k * v <= j; k ++ )
f[j] = max(f[j], f[j - k * v] + k * w);
}
cout << f[m] << endl;
return 0;
}
AcWing 5. Multiple knapsack problem II
State calculation
f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i − 1 , j − k ∗ v ) + k ∗ w ) f(i, j) = max(f(i - 1, j), f(i - 1, j - k * v) + k * w) f(i,j)=max(f(i−1,j),f(i−1,j−k∗v)+k∗w)
optimization
f
(
j
)
=
m
a
x
(
f
(
j
)
,
f
(
j
−
k
∗
v
)
+
k
∗
w
)
f(j) = max(f(j), f(j - k * v) + k * w)
f(j)=max(f(j),f(j−k∗v)+k∗w)
Then optimize
Using the binary method of thinking, the items are
1
,
2
,
4
,
8
,
.
.
.
1, 2, 4, 8, ...
1, 2, 4, 8
0001
,
0010
,
0100
,
1000
0001, 0010, 0100,1000
The binary sequence of 0001001000 packs the articles, and the extra articles are packed into one piece alone.
For example:
11
=
1
+
2
+
4
+
4
11 = 1 + 2 + 4 + 4
11 = 1 + 2 + 4 + 4, then use
1
,
2
,
4
,
4
1, 2, 4, 4
The numbers 1,2,4,4 can be expressed
11
11
All numbers within 11
For example:
10
=
2
+
4
+
4
10 = 2 + 4 + 4
10=2+4+4,
9
=
1
+
4
+
4
9 = 1 + 4 + 4
9=1+4+4,
8
=
4
+
4
8 = 4 + 4
8 = 4 + 4,... Other numbers are the same
In this way, as long as each packaged item group chooses to take it or not, the multi knapsack problem can be abstracted into 01 knapsack problem, which reduces the time complexity
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 25000;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
int cnt = 0;
for(int i = 1; i <= n; i ++)
{
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while(k <= s)
{
cnt ++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if(s > 0)
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for(int i = 1; i <= n; i ++ )
for(int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
AcWing 9. Grouping knapsack problem
State representation
f ( i , j ) f(i, j) f(i,j) represents the optimal solution in the first i group of articles under volume j
State calculation
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
(
i
,
k
)
)
+
w
(
i
,
k
)
)
)
f(i, j) = max(f(i - 1, j), f(i - 1, j -v(i, k)) + w(i, k)))
f(i,j)=max(f(i−1,j),f(i−1,j−v(i,k))+w(i,k)))
Equivalent deformation
f
(
j
)
=
m
a
x
(
f
(
j
)
,
f
(
j
−
v
(
i
,
k
)
+
w
(
i
,
k
)
)
)
f(j) = max(f(j), f(j - v(i, k) + w(i, k)))
f(j)=max(f(j),f(j−v(i,k)+w(i,k)))
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++)
{
cin >> s[i];
for(int j = 0; j < s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for(int i = 1; i <= n; i ++ )
for(int j = m; j >= 0; j -- )
for(int k = 0; k < s[i]; k ++ )
if(v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}
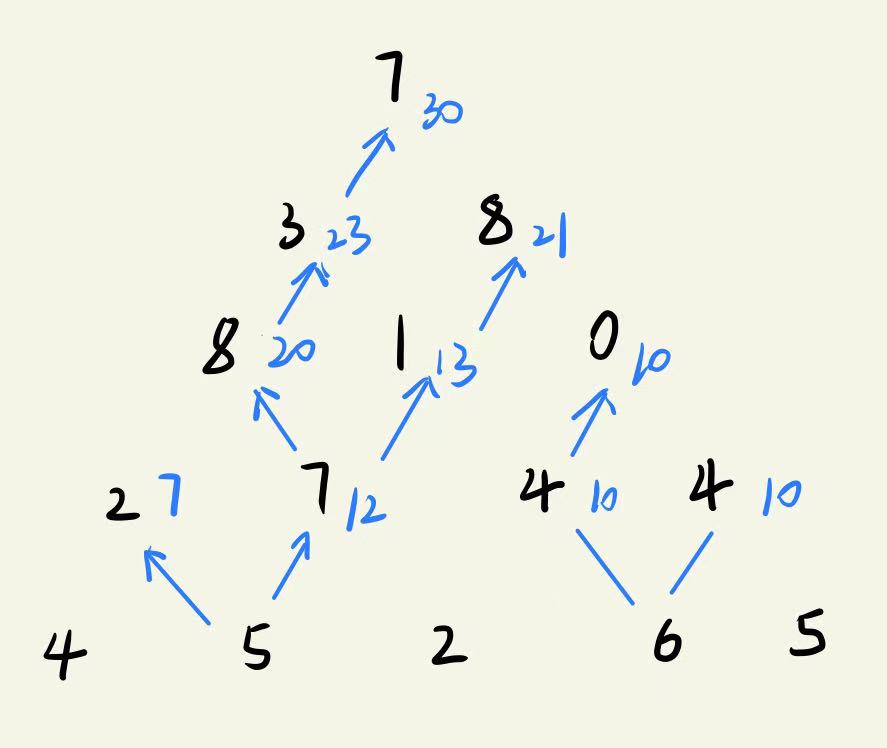
AcWing 898. Digital triangle
You can select the larger value of the lower two numbers from bottom to top plus your own value until the top of the triangle is the desired value
It can also be operated from top to bottom
#include<iostream>
using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N][N];
int f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= i; j ++ )
scanf("%d", &a[i][j]);
for(int i = 0; i <= n; i ++)
for(int j = 0; j <= i + 1; j ++)
f[i][j] = -INF;
f[1][1] = a[1][1];
for(int i = 2; i <= n; i ++ )
for(int j = 1; j <= i; j ++)
f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
int res = -INF;
for(int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
printf("%d\n", res);
return 0;
}
AcWing 895. Longest ascending subsequence
State representation
f [ i ] f[i] f[i] is represented by a [ i ] a[i] a[i] length value of the longest ascending subsequence at the end
State calculation
f
[
i
]
=
m
a
x
(
f
[
i
]
,
f
[
j
]
+
1
)
,
i
f
a
[
j
]
<
a
[
i
]
f[i] = max(f[i], f[j] + 1), ~~~if~~~a[j] < a[i]
f[i]=max(f[i],f[j]+1), if a[j]<a[i]
r
e
s
=
m
a
x
(
f
[
i
]
)
res = max(f[i])
res=max(f[i])
Example:
a: 3 1 2 1 8 5 6 f: 1 1 2 1 3 3 4
#include<iostream>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++ )
{
f[i] = 1;
for(int j = 1; j < i; j ++ )
if(a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for(int i = 1; i <= n; i ++ ) res = max(res, f[i]);
printf("%d\n", res);
return 0;
}
AcWing 896. Longest ascending subsequence II
#include<iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int st[N];
int tt = 0;
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
st[tt] = a[0];
for(int i = 1 ; i < n ; i++)
{
//If the element is larger than the top element of the stack, put the element on the stack
if(a[i] > st[tt]) st[++ tt] = a[i];
//Replace the first number greater than or equal to this number
else
{
int l = 0 , r = tt;
while(l < r)
{
int mid = (l + r) >> 1;
if(st[mid] >= a[i]) r = mid;
else l = mid + 1;
}
st[l] = a[i];
}
}
printf("%d",tt + 1);
return 0;
}
This stack is not used to record the final longest subsequence, but the substring ending with stk[i] has the longest length of I or the smallest ending element in the incremental substring with length of I. After understanding this problem, we will know why the new element is either added at the end or replaces the position of the first element greater than or equal to it.
The substitution here contains a greedy idea. For substrings of the same length, we certainly hope that the smaller the end, the better, so that there are more opportunities to expand in the future.
AcWing 897. Longest common subsequence
State representation
f [ i ] [ j ] f[i][j] f[i][j] represents the length of the longest common subsequence between the first I characters of a and the first j characters of b
State calculation
-
a
[
i
]
!
=
b
[
j
]
a[i] ~!= ~b[j]
a[i] != b[j]
a[i] is not in the longest common subsequence, f [ i − 1 ] [ j ] f[i - 1][j] f[i−1][j]
b[j] is not in the longest common subsequence, f [ i ] [ j − 1 ] f[i][j - 1] f[i][j−1] - a [ i ] = = b [ j ] a[i] ~==~ b[j] a[i] == b[j], f [ i − 1 ] [ j − 1 ] + 1 f[i - 1][j - 1] + 1 f[i−1][j−1]+1
state transition
- f [ i ] [ j ] = m a x ( f [ i − 1 ] [ j ] , f [ i ] [ j − 1 ] ) ; f[i][j] = max(f[i - 1][j], f[i][j - 1]); f[i][j]=max(f[i−1][j],f[i][j−1]);
- f [ i ] [ j ] = m a x ( f [ i ] [ j ] , f [ i − 1 ] [ j − 1 ] + ( a [ i ] = = b [ j ] ) ) ; f[i][j] = max(f[i][j], f[i - 1][j - 1] + (a[i] == b[j])); f[i][j]=max(f[i][j],f[i−1][j−1]+(a[i]==b[j]));
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
scanf("%s%s", a + 1, b + 1);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if(a[i] == b[j])
f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
printf("%d\n", f[n][m]);
return 0;
}
AcWing 902. Minimum editing distance
State representation
f [ i ] [ j ] f[i][j] f[i][j] represents the minimum number of operations to convert the first I characters of string a into the first j characters of string b
State calculation
- Delete operation: after deleting a[i], the first i - 1 characters of a are the same as the first j characters of b, f [ i − 1 ] [ j ] + 1 f[i -1][j] + 1 f[i−1][j]+1
- Insert operation: before inserting b[j], the first i characters of a are the same as the first j - 1 characters of b, f [ i ] [ j − 1 ] + 1 f[i][j -1] + 1 f[i][j−1]+1
- Modification: before modifying a[i] to b[j], the first i - 1 character of a is the same as the first j - 1 character of b
If a[i] == b[j], f [ i − 1 ] [ j − 1 ] + 0 f[i - 1][j - 1] + 0 f[i − 1][j − 1] + 0, otherwise a [i]= b[j], f [ i − 1 ] [ j − 1 ] + 1 f[i - 1][j - 1] + 1 f[i−1][j−1]+1
State transition equation
- f [ i ] [ j ] = m i n ( f [ i − 1 ] [ j ] , f [ i ] [ j − 1 ] ) + 1 ; f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1; f[i][j]=min(f[i−1][j],f[i][j−1])+1;
- f [ i ] [ j ] = m i n ( f [ i ] [ j ] , f [ i − 1 ] [ j − 1 ] + ( a [ i ] ! = b [ j ] ) ) ; f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j])); f[i][j]=min(f[i][j],f[i−1][j−1]+(a[i]!=b[j]));
initialization
- f [ 0 ] [ i ] = i ; f[0][i] = i; f[0][i]=i; If the length of a is 0 and becomes the first I characters of b, I characters need to be added
- f [ i ] [ 0 ] = i ; f[i][0] = i; f[i][0]=i; The length of b is 0. If it becomes the first I characters of b, I characters need to be deleted
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%s", &n, a + 1);
scanf("%d%s", &m, b + 1);
for( int i = 0; i <= m; i ++ ) f[0][i] = i;
for( int i = 0; i <= n; i ++ ) f[i][0] = i;
for( int i = 1; i <= n; i ++ )
for( int j = 1; j <= m; j ++ )
{
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + 1;
f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
}
printf("%d\n", f[n][m]);
return 0;
}
AcWing 899. Edit distance
The idea is the same as AcWing 902. Shortest editing distance
#include<iostream>
#include<string.h>
using namespace std;
const int N = 15, M = 1010;
int n, m;
int f[N][N];
char str[M][N];
int edit_distance(char a[], char b[])
{
int la = strlen(a + 1), lb = strlen(b + 1);
for(int i = 0; i <= lb; i ++ ) f[0][i] = i;
for(int i = 0; i <= la; i ++ ) f[i][0] = i;
for(int i = 1; i <= la; i ++ )
for(int j = 1; j <= lb; j ++ )
{
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
}
return f[la][lb];
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < n; i ++ ) scanf("%s", str[i] + 1);
while(m -- )
{
char s[N];
int limit;
scanf("%s%d", s + 1, &limit);
int res = 0;
for(int i = 0; i < n; i ++ )
if(edit_distance(str[i], s) <= limit)
res ++;
printf("%d\n", res);
}
return 0;
}
AcWing 282. Stone merging
Because only two adjacent piles of stones can be merged, it is not Huffman algorithm and greed cannot be used.
State representation
f [ i ] [ j ] f[i][j] f[i][j] represents the minimum cost of merging the i-th pile of stones to the j-th pile of stones into one pile of stones
State calculation
f
[
i
]
[
j
]
=
m
i
n
(
f
[
i
]
[
k
]
+
f
[
k
+
1
]
[
j
]
+
s
[
j
]
−
s
[
i
−
1
]
)
f[i][j]=min(f[i][k] + f[k + 1][j] + s[j] - s[i - 1])
f[i][j]=min(f[i][k]+f[k+1][j]+s[j]−s[i−1])
k
∈
[
i
,
j
−
1
]
k ∈[i,j - 1]
k∈[i,j−1]
boundary condition
f
[
i
]
[
i
]
=
0
f[i][i] = 0
f[i][i]=0, the same pile of stones does not need to be merged
The cost of merging these stones is
f
[
1
]
[
n
]
f[1][n]
f[1][n]
#include<iostream>
using namespace std;
const int N = 310;
int n;
int s[N];
int f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);
//Prefix and for easy calculation
for(int i = 1; i <= n; i ++ ) s[i] += s[i - 1];
for(int len = 2; len <= n; len ++ ) //len is the interval length
for(int i = 1; i + len - 1 <= n; i ++ ) //
{
int l = i, r = i + len - 1; //l is the starting point and r is the end point
f[l][r] = 0x3f3f3f3f;
for(int k = l; k < r; k ++ ) //k is the dividing point for state calculation
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
}
printf("%d\n", f[1][n]);
return 0;
}
AcWing 900. Integer partition
This problem can be abstracted into a complete knapsack problem
The numbers 1, 2, 3,..., n are regarded as the volume of n objects. Each object can be used for unlimited times. There are several schemes to fill the backpack with volume n
State representation
f ( i , j ) f(i, j) f(i,j) indicates front i i i integers ( 1 , 2 , 3 , . . . , i ) (1, 2, 3, ..., i) (1,2,3,...,i) just spell it into an integer j j Number of schemes j
State calculation
The set values of 0 i, 1 i, 2 i,... Selected in each set are accumulated
- f ( i , j ) = f ( i − 1 , j ) + f ( i − 1 , j − i ) + f ( i − 1 , j − 2 ∗ i ) + f ( i − 1 , j − 3 ∗ i ) + . . . f(i, j) = f(i - 1, j) + f(i - 1, j - i) + f(i - 1, j - 2 * i) + f(i - 1, j - 3 * i) + ... f(i,j)=f(i−1,j)+f(i−1,j−i)+f(i−1,j−2∗i)+f(i−1,j−3∗i)+...
- f ( i , j − i ) = f ( i − 1 , j − i ) + f ( i − 1 , j − 2 ∗ i ) + f ( i − 1 , j − 3 ∗ i ) + . . . f(i,j - i) =~~~~~~~~~~~~~~~~ f(i - 1, j - i) + f(i - 1,j - 2 * i) + f(i - 1, j - 3 * i) + ... f(i,j−i)= f(i−1,j−i)+f(i−1,j−2∗i)+f(i−1,j−3∗i)+...
Get: f ( i , j ) = f ( i , j − i ) + f ( i − 1 , j ) f(i, j) = f(i, j - i) + f(i-1, j) f(i,j)=f(i,j−i)+f(i−1,j)
boundary condition
f [ 1 ] [ 1 ] = 1 f[1][1] = 1 f[1][1]=1
Equivalent deformation
f
(
j
)
=
f
(
j
)
+
f
(
j
−
i
)
f(j) = f(j ) + f(j - i)
f(j)=f(j)+f(j−i)
boundary condition
f
[
0
]
=
1
f[0] = 1
f[0]=1, the capacity is 0, and none of the first i numbers is selected
#include<iostream>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N][N];
int main()
{
cin >> n;
f[1][1] = 1;
for(int i = 2; i <= n; i ++ )
for(int j = 1; j <= i; j ++ )
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int res = 0;
for(int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;
}
Equivalent deformation
#include<iostream>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N];
int main()
{
cin >> n;
f[0] = 1;
for(int i = 1; i <= n; i ++ )
for(int j = i; j <= n; j ++ )
f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;
return 0;
}
AcWing 338. Counting problem
seek
[
a
,
b
]
[a, ~b]
[a, b] Number in interval
k
(
k
∈
[
0
,
9
]
)
k(k ∈[0, 9])
The number of occurrences of k (k ∈ [0,9]),
You can turn this problem into finding numbers
k
k
k in interval
[
0
,
a
]
[0, a]
The number of occurrences in [0,a] is recorded as
c
o
u
n
t
(
b
)
count(b)
count(b),
And in interval
[
0
,
b
]
[0, b]
The number of occurrences of [0,b] is recorded as
c
o
u
n
t
(
b
)
count(b)
count(b),
c
o
u
n
t
(
b
)
−
c
o
u
n
t
(
a
)
count(b) - count(a)
count(b) − count(a) is the number of occurrences of the desired number
The idea is similar to prefixes and
Example:
Given number
n
=
a
b
c
d
e
f
n = abcdef
n=abcdef find the number of times the number x appears in the fourth digit
Classified discussion
- 1 the size range of the first three digits is in the interval [ 0 , a b c − 1 ] [0, abc - 1] In [0,abc − 1], the fourth digit is x x x. The number of occurrences is ( a b c − 1 + 1 ) ∗ 100 (abc - 1 + 1) * 100 (abc−1+1)∗100
- 2. The first three digits are equal to
a
b
c
abc
abc the fourth digit should be
x
x
x. Then the conditions to be met are
d
>
=
x
d >= x
d>=x
① d < x d < x D < x: the last two digits, and the fourth digit is x, which is greater than a b c d e f abcdef abcdef, no solution
② d = = x d == x d==x: the fourth digit is x x The value range of the last two digits of x is [ 0 , e f ] [0, ef] [0,ef], the number is e f + 1 ef + 1 ef+1
③ d > x d~ > ~x d > x: The fourth is x x The value range of the last two digits of x is [ 0 , 99 ] [0, 99] [0,99], the number is 100
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
//Intercept the l ~ r digits of num
int get(vector<int> num, int l, int r)
{
int res = 0;
for(int i = l; i >= r; i -- ) res = res * 10 + num[i];
return res;
}
//Calculate the x-Power of 10
int power10(int x)
{
int res = 1;
while (x -- ) res *= 10;
return res;
}
int count(int n, int x)
{
if (!n) return 0;
//The number n is stored in an array to get the number on each bit
vector<int> num;
while (n)
{
num.push_back(n % 10);
n /= 10;
}
n = num.size();
int res = 0;
//The highest bit cannot be 0. When x == 0, you can cycle less once
//Calculate the number of times x appears on each number, and add up to the total number of times
for (int i = n - 1 - !x; i >= 0; i -- )
{
// When i == n - 1, it is a bit of a number and does not need to be multiplied by the power of 10
if (i < n - 1)
{
//abc * power10(i)
res += get(num, n - 1, i + 1) * power10(i);
//When calculating the number of occurrences of 0, the first digit cannot be 0
//That is, when x == 0, abc cannot be 000
if (!x) res -= power10(i);
}
//d == x
if (num[i] == x) res += get(num, i - 1, 0) + 1;
// D > x
else if (num[i] > x) res += power10(i);
}
cout << num[n - 1] << " ";
return res;
}
int main()
{
int a, b;
while (cin >> a >> b , a)
{
if (a > b) swap(a, b);
for (int i = 0; i <= 9; i ++ )
cout << count(b, i) - count(a - 1, i) << ' ';
cout << endl;
}
return 0;
}
AcWing 291. Mondrian's dream
When the small squares placed horizontally are placed, the remaining positions can only be placed vertically, so the total number of placement schemes for small squares on the chessboard is equal to the number of schemes for small squares placed horizontally
State representation
f ( i , j ) f(i, j) f(i,j) indicates front i − 1 i - 1 Column i − 1 has been placed and extended to the third column i i The status of column i is j j All schemes of j, where j j j is a binary number, which is used to indicate which row of small squares are placed horizontally. The number of digits is consistent with the number of rows on the chessboard. 1 indicates which rows of small squares are extended horizontally, and 0 indicates which rows are not extended horizontally.
State calculation
-
state transition
The first i i Column i is fixed, first from the second column i − 2 i - 2 i − 2 train transferred to i − 1 i - 1 Starting from column i − 1, it is assumed that the status at this time is k k k. The number of schemes corresponding to it should be f ( i − 1 , k ) f(i -1, k) f(i − 1,k), i.e. front i − 2 i - 2 Column i − 2 is finished, and from i − 2 i - 2 i − column 2 extends to the second column i − 1 i - 1 The status of column i − 1 is k k Number of all schemes of k.
k. The following requirements shall be met:
1.1. k & j = = 0 k ~\& ~j == 0 k & j==0, i.e k k k and j j j is not a small square placed horizontally in the same row, and the small squares placed between them will not conflict
1.2. After the horizontal small squares are placed, the remaining empty positions are reserved for the vertical small squares, and the length should be even. -
The expression for the final answer should be f [ m ] [ 0 ] f[m][0] f[m][0], indicates the second m − 1 m - 1 m − 1 column has been placed, and the second column m m Column m has no small box protruding, and its status represents the value of k = 0 k = 0 k=0
-
State calculation
f [ i ] [ j ] + = f [ i − 1 ] [ k ] f[i][j] += f[i - 1][k] f[i][j]+=f[i − 1][k], where i ∈ [ 1 , m ] , j ∈ [ 0 , 1 < < n ] , k ∈ s t a t e [ j ] i ∈[1, m], j∈[0, 1 << n], k∈state[j] i∈[1,m],j∈[0,1<<n],k∈state[j] -
boundary condition
f [ 0 ] [ 0 ] = 1 f[0][0] = 1 f[0][0]=1
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
//Each column and each space can be put or not, so it is 2 ^ N
const int N = 12, M = 1 << N;
int n, m;
LL f[N][M];
// Record the binary sequence of each successful state transition
vector<int> state[M];
/* The status from column i-2 to column i-1 is k,
* Whether it can be successfully transferred to column i-1, and the status extending to column i is j
* st[j|k]=true Indicates successful transfer
*/
bool st[M];
int main()
{
while (cin >> n >> m, n || m)
{
//Preprocess the st array to find the state with an even number of spaces
for (int i = 0; i < 1 << n; i ++ )
{
//Record the number of 0 in the current column state
int cnt = 0;
bool is_valid = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
{
//The number of spaces is odd
if (cnt & 1)
{
is_valid = false;
break;
}
cnt = 0;
}
else cnt ++ ;
//The number of spaces is odd
if (cnt & 1) is_valid = false;
st[i] = is_valid;
}
//Record the status that can be transferred legally
//That is, the small box protruding from column i - 1 will not conflict with column i
for (int i = 0; i < 1 << n; i ++ )
{
state[i].clear();
for (int j = 0; j < 1 << n; j ++ )
//Indicates that it is legal in the case of k column state i and k - 1 column state j
if ((i & j) == 0 && st[i | j])
state[i].push_back(j);
}
//State calculation
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= m; i ++ )
for (int j = 0; j < 1 << n; j ++ )
for (auto k : state[j])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl;
}
return 0;
}
AcWing 91. Shortest Hamilton path
The binary sequence is used to represent all passing points
For example, walk past the point
0
,
1
,
2
,
4
0,1,2,4
0, 1, 2 and 4 are represented as
10111
10111
10111, go
0
,
2
,
3
0,2,3
0, 2 and 3 are represented as
01101
01101
01101
State representation
f ( i , j ) f(i, j) f(i,j) denotes all arrival points j j j. And all the points passed are i i All path lengths of i
State calculation
f [ i ] [ j ] = m i n ( f [ i ] [ j ] , f [ i − ( 1 < < j ) ] [ k ] + w [ k ] [ j ] ) f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]) f[i][j]=min(f[i][j],f[i−(1<<j)][k]+w[k][j])
among i ∈ [ 0 , 1 < < n ] , j ∈ [ 0 , n − 1 ] , k ∈ [ 0 , n − 1 ] i∈[0, 1 << n], j ∈ [0, n -1], k∈[0, n - 1] i∈[0,1<<n],j∈[0,n−1],k∈[0,n−1]
Boundary conditions:
f
[
1
]
[
0
]
=
0
;
f[1][0] = 0;
f[1][0]=0;
Final result:
f
[
(
1
<
<
n
)
−
1
]
[
n
−
1
]
f[(1 << n) - 1][n - 1]
F [(1 < < n) − 1][n − 1], indicates
(
1
<
<
n
)
−
1
(1 << n) - 1
(1 < < n) − 1 each point passes through,
n
−
1
n - 1
n − 1 indicates reaching the end point
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20, M = 1 << N;
int n;
int w[N][N];
int f[M][N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
cin >> w[i][j];
memset(f, 0x3f, sizeof f); //Initialize to a larger constant
f[1][0] = 0; //The starting point does not cost anything
for (int i = 0; i < 1 << n; i ++ ) //Enumerate all paths
for (int j = 0; j < n; j ++ ) //Enumerate all points
if (i >> j & 1) //Does path i pass through point j
for (int k = 0; k < n; k ++ ) //Enumerate the point k of j
if (i >> k & 1) //Judge whether the point k reaching j is the optimal path
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n) - 1][n - 1] << endl; //Output final answer
return 0;
}
AcWing 285. A dance without a boss
Status indication:
f
[
u
]
[
0
]
f[u][0]
f[u][0]: the maximum happiness value in the absence of u in the subtree with u as the root node
f
[
u
]
[
1
]
f[u][1]
f[u][1]: in the subtree with u as the root node, the maximum happiness value of u is present
Status calculation:
- When the u node is not selected, the child node selects the case where the happiness value is the largest
f [ u ] [ 0 ] + = m a x ( f [ j ] [ 0 ] , f [ j ] [ 1 ] ) f[u][0] += max(f[j][0], f[j][1]) f[u][0]+=max(f[j][0],f[j][1]) - When u node is selected, child nodes must not be selected
f [ u ] [ 1 ] + = ( f [ j ] [ 0 ] ) f[u][1] += (f[j][0]) f[u][1]+=(f[j][0])
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 6010;
int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
bool has_father[N]; //Mark whether there is a direct supervisor
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
//When the boss is, add the happiness value of the boss
f[u][1] = happy[u];
for(int i = h[u]; ~i; i = ne[i])
{
int j = e[i]; //Child node
dfs(j); //Search child nodes
//If the boss is absent, select the maximum value of direct subordinates to go or not to go
f[u][0] += max(f[j][0], f[j][1]);
//When the boss is, plus the happiness value that the direct subordinates don't go
f[u][1] += f[j][0];
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ ) cin >> happy[i];
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; i ++ )
{
int a, b;
cin >> a >> b;
has_father[a] = true;
add(b, a);
}
int root = 1;
while(has_father[root]) root ++ ;
dfs(root);
//Take the maximum value of whether the root node can go or not
cout << max(f[root][0], f[root][1]);
return 0;
}
AcWing 901. Skiing
Memory search is similar to search and is an implementation of DP
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int N = 310;
int n, m;
int h[N][N];
int f[N][N];
//Offset to offset the current coordinate
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int dp(int x, int y)
{
int& v = f[x][y];
//This point has been traversed
if(v != -1) return v;
v = 1;
//The idea is similar to BFS
for(int i = 0; i < 4; i ++ )
{
int a = x + dx[i], b = y + dy[i];
//Ensure that the current coordinate value is not out of bounds and the corresponding height can slide down
//In this step, you can record the maximum value corresponding to the traversed coordinates into the f array
if(a >= 1 && a <= n && b >= 1 && b <= m && h[a][b] < h[x][y])
v = max(v, dp(a, b) + 1);
}
return v;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
cin >> h[i][j];
memset(f, -1, sizeof f);
int res = 0, x, y;
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
{
if(res < dp(i, j)) {
res = dp(i, j);
x = i, y = j;
}
}
cout << res << endl;
// //Output path
// queue<pair<int, int>> q;
// vector<pair<int, int>> path;
// q.push({x, y});
// while(!q.empty()) {
// auto t = q.front();
// path.push_back(t);
// q.pop();
// x = t.first, y = t.second;
// for(int i = 0; i < 4; i ++ ) {
// auto a = x + dx[i], b = y + dy[i];
// if(a >= 1 && a <= n && b >= 1 && b <= m && h[a][b] == h[x][y] - 1)
// q.push({a, b});
// }
// }
// for(auto i : path) {
// cout << i.first << " " << i.second << endl;
// }
}