Balanced Tree and FHQ-Treap
A balanced tree (i.e. a balanced binary search tree) is a series of metaphysical operations that keep the binary search tree (BST) in a more balanced state and prevent it from degenerating under certain data (when BST has monotonic insertion values, the tree is unbalanced and degenerates into \(\mathcal{O}(n)\) once).Common balance trees are Treap, FHQ-Treap, Splay, AVL, red and black trees, etc.Balance trees are widely used to maintain collections, columns, auxiliary LCT s, and so on.
FHQ-Treap is a balanced tree with smaller constants, smaller code sizes and more functions.It maintains the balance by splitting and merging and determining the merge scheme based on the random weights of the nodes during merging.Single Complexity(\mathcal{O}(\log n)\).
Node Information - Basic Operations
int s[N];//s[i] Subtree size with I as root int r[N];//Random weights of r[i]node I int v[N];//Weight value of v[i] node i int ch[N][2];//Left son of ch[i][0] node i and right son of ch[i][1] node i int siz;//Used node tree, note that it is not the size of the tree int rt;//Root Node Number int New(int val) {s[++siz] = 1; r[siz] = rand(); v[siz] = val; return siz;}//Create a new node and return its number void upd(int p) {s[p] = s[ch[p][0]] + s[ch[p][1]] + 1;}//Update subtree size
Merge & Split
- Merge (x,y) merges two trees rooted by X and Y into one and returns the merged root node number.All arbitrary weights in a tree with X as its root are not greater than all arbitrary weights in a tree with y as its root.
We can do this recursively.To achieve a balance, we need to use random weights.The merge scheme is determined by comparing the random weights of x and y nodes.
- Both x, y trees are not empty:
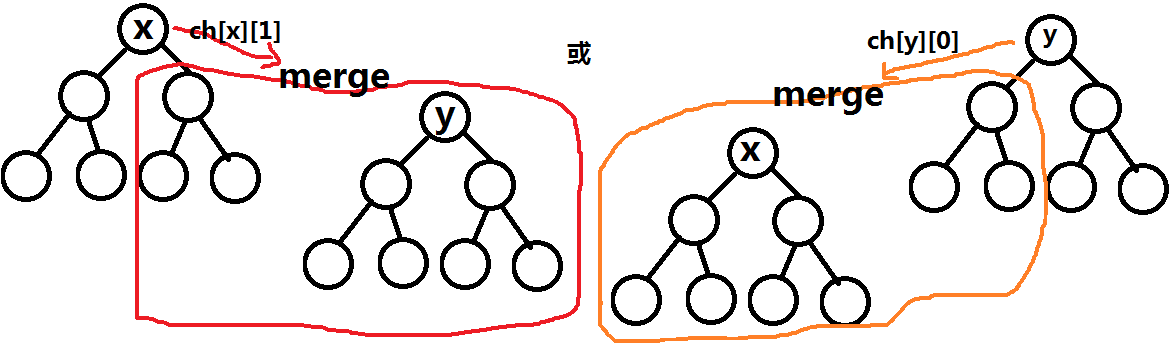
- x,y are empty: return 0 directly.
- Empty-one-not-empty time in x,y: Returns the root node of a non-empty tree, using bitwise or implementation in bitwise operations.
Note that all arbitrary weights in a tree rooted with x are not greater than all arbitrary weights in a tree rooted with y.
int merge(int x, int y) { if(!x || !y) return x | y; return r[x] < r[y] ? (ch[x][1] = merge(ch[x][1], y), upd(x), x) : (ch[y][0] = merge(x, ch[y][0]), upd(y), y); }
- split(p, val, x, y) divides a tree with P as its root into two trees, X and y as its roots.Where the weight of all nodes in the X-tree is less than or equal to val, and the weight of all nodes in the y-tree is greater than val.
If the weight of node p \(\le val\), then both the weight of the left subtree of p and p \(\le val\), they must belong to the x-tree.Give the p node and the left subtree of p to x, and then continue to split within the right subtree of p.
Conversely, if the node p has a weight (>val\), then both the right subtree of p and p have a weight (>val\), which must belong to the y-tree.Give the p node and the right subtree of p to y, and then continue to split within the left subtree of p.
void split(int p, int val, int &x, int &y) { if(!p) {x = y = 0; return;} v[p] <= val ? (x = p, split(ch[p][1], val, ch[p][1], y)) : (y = p, split(ch[p][0], val, x, ch[p][0])); upd(p); }
- split(p, sss, x, y) divides a tree with P as its root into two trees with X and y as its roots.The X-tree is a tree (split by size) composed of the first SSS nodes sequentially traversed in the p-tree.
Similar to the idea of splitting by weight.When walking to the right subtree, subtract the size of the left subtree and the root node (left subtree size + 1) because this size is relative to the subtree rooted at the current node.
void split(int p, int sss, int &x, int &y) { if(!p) {x = y = 0; return;} if(sss > s[ch[p][0]]) x = p, split(ch[p][1], sss - s[ch[p][0]] - 1, ch[p][1], y); else y = p, split(ch[p][0], sss, x, ch[p][0]); upd(p); }
insert
Set the number of inserts to \(val\), split X and y by \(val-1\), and then create a new node P with a new weight of \(val\).Merge x, p, y in turn.
void insert(int val) { int x, y; split(rt, val - 1, x, y); rt = merge(merge(x, New(val)), y); }
Insert at a given location: change splitting by weight to splitting by size.
in void ins(int l, char val) {//Insert node with val ue after l position int x, y; split(rt, l, x, y); rt = merge(merge(x, New(val)), y); }
delete
Set the number of deletions to \(val\), first press \(val\) to split y and z, then press \(val-1\) to split y into x and y.If y is not empty, there is a number with a value of \(val\).If only one is deleted, set Y as the result of the merge of the left and right sons of y, and merge x, y, and Z in turn; if you delete all the numbers whose values are \(val\), merge X and Z directly.
void erase(int val) { int x, y, z; split(rt, val, x, z); split(x, val - 1, x, y); if(y) y = merge(ch[y][0], ch[y][1]); rt = merge(merge(x, y), z); } /* void erase_all(int val) { int x, y, z; split(rt, val, x, z); split(x, val - 1, x, y); rt = merge(x, z); } */
Interval deletion: Split the target tree and merge other trees to get the deleted tree.
void eraselr(int l, int r) { int x, y, z; split(rt, r, y, z); split(y, l - 1, x, y); rt = merge(x, z); }
Ranking of Lookup Values
Rank is defined as the number of smaller numbers plus one.When a tree with a smaller weight is split, the answer is the tree size + 1.
int rank(int val) { int x, y, ans; split(rt, val - 1, x, y); ans = s[x] + 1; rt = merge(x, y); return ans; }
Find values by rank
From the root node, the size of the subtree determines whether the target is the current node or where to go.When walking to the right subtree, subtract the size of the left subtree and the root node (left subtree size + 1) because this ranking is relative to the subtree rooted at the current node.
int val(int rk) { int p = rt; while(p) { if(s[ch[p][0]] + 1 == rk) return v[p]; else if(rk <= s[ch[p][0]]) p = ch[p][0]; else rk = rk - s[ch[p][0]] - 1, p = ch[p][1]; } }
Precursor-successor
Precursor: less than \(x\) and the largest number
Succession: greater than \(x\), and the smallest number
Following this line of thought, we just need to split the tree that satisfies the first half sentence, and then we can easily get the nodes that satisfy the second half sentence in this tree.
int prev(int val) { int x, y, tmp; split(rt, val - 1, x, y); tmp = x; while(ch[tmp][1]) tmp = ch[tmp][1]; rt = merge(x, y); return v[tmp]; } int next(int val) { int x, y, tmp; split(rt, val, x, y); tmp = y; while(ch[tmp][0]) tmp = ch[tmp][0]; rt = merge(x, y); return v[tmp]; }
Maintenance interval
FHQ-Treap can also be used to maintain intervals.If we make the position of nodes in the true sequence satisfy the BST property, then the real sequence is the middle-order traversal of the tree.Generally, FHQ-Treap performs an interval modification/query by splitting out the target tree - > modification/query (generally using lazy markers like segment trees) - > merging.This is going to split up by size.
Unlike segment trees, FHQ-Treap supports insertion/deletion at any location, interval flipping, and so on, but with a large constant.
For each operation \([l,r]\), we first split the target tree by size.This is done by first splitting out\(y=[1,r]\) and \(z=[r+1,n]\), then splitting y out\(x=[1,l-1]\) and \(y=[l,r]\).At this point y is the target tree.
Then we mark y as lazy.Note that markers are downloaded when splitting/merging.The method of downloading tags depends on the situation.
Example
All operations were described earlier.
#include <cstdio> #include <cstring> #include <ctime> #include <cstdlib> #include <algorithm> using namespace std; #define in __inline__ #define rei register int char inputbuf[1 << 23], *p1 = inputbuf, *p2 = inputbuf; #define getchar() (p1 == p2 && (p2 = (p1 = inputbuf) + fread(inputbuf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++) in int read() { register int res = 0; char ch = getchar(); bool f = true; for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = false; for(; ch >= '0' && ch <= '9'; ch = getchar()) res = res * 10 + (ch ^ 48); return f ? res : -res; } in void write(register int x){ static unsigned char _q[35]; register unsigned char t=0; for(; x; x /= 10) _q[++t] = x % 10; for(; t; --t) putchar(_q[t] + 48); putchar(32); } in void swap(int &x, int &y) {x ^= y ^= x ^= y;}
const int N = 1e5 + 5; int ch[N][2], s[N], r[N], v[N], siz, rt; int New(int val) {s[++siz] = 1; r[siz] = rand(); v[siz] = val; return siz;} void upd(int p) {s[p] = s[ch[p][0]] + s[ch[p][1]] + 1;} int merge(int x, int y) { if(!x || !y) return x | y; if(r[x] > r[y]) {ch[x][1] = merge(ch[x][1], y); upd(x); return x;} else {ch[y][0] = merge(x, ch[y][0]); upd(y); return y;} } void split(int p, int val, int &x, int &y) { if(!p) {x = y = 0; return;} v[p] <= val ? (x = p, split(ch[p][1], val, ch[p][1], y)) : (y = p, split(ch[p][0], val, x, ch[p][0])); upd(p); } in void insert(int val) { int x, y; split(rt, val - 1, x, y); rt = merge(merge(x, New(val)), y); } in void erase(int val) { int x, y, z; split(rt, val, x, z); split(x, val - 1, x, y); if(y) y = merge(ch[y][0], ch[y][1]); rt = merge(merge(x, y), z); } in int rank(int val) { int x, y, ans; split(rt, val - 1, x, y); ans = s[x] + 1; rt = merge(x, y); return ans; } in int val(int rk) { int p = rt; while(p) { if(s[ch[p][0]] + 1 == rk) return v[p]; else if(rk <= s[ch[p][0]]) p = ch[p][0]; else rk = rk - s[ch[p][0]] - 1, p = ch[p][1]; } } in int prev(int val) { int x, y, tmp; split(rt, val - 1, x, y); tmp = x; while(ch[tmp][1]) tmp = ch[tmp][1]; rt = merge(x, y); return v[tmp]; } in int next(int val) { int x, y, tmp; split(rt, val, x, y); tmp = y; while(ch[tmp][0]) tmp = ch[tmp][0]; rt = merge(x, y); return v[tmp]; } int main() { int q = read(), opt, x, lst = 0, ans = 0; srand(time(0)); for(; q; --q) { opt = read(), x = read(); if(opt == 1) insert(x); else if(opt == 2) erase(x); else if(opt == 3) write(rank(x))); else if(opt == 4) write(val(x)); else if(opt == 5) write(prev(x)); else write(next(x)); } }
We can obviously get a property: flipping the same interval an even number of times equals not flipping.So we can use XOR operations (\(0\operatorname{xor}\) to get \(1\) odd times and \(0\) even times.
Violently flipping the whole target tree means swapping left and right sons for each node. Update the left and right sons when you download the tag and swap the left and right sons.
The final answer is the sequence from sequential traversal throughout the tree.Tags are also downloaded when outputting recursively.
const int N = 1e5 + 5; int s[N], ch[N][2], r[N], v[N], siz, rt, n, m, t[N]; in void push(int p) { if(!t[p]) return; swap(ch[p][0], ch[p][1]); if(ch[p][0]) t[ch[p][0]] ^= 1; if(ch[p][1]) t[ch[p][1]] ^= 1; t[p] = 0; } in int New(int val) { v[++siz] = val; s[siz] = 1; r[siz] = rand(); return siz; } in void upd(int p) {s[p] = s[ch[p][0]] + s[ch[p][1]] + 1;} void print(int p) { if(!p) return; push(p); print(ch[p][0]); write(v[p]); print(ch[p][1]); } int merge(int x, int y) { if(!x || !y) return x | y; return r[x] < r[y] ? (push(x), ch[x][1] = merge(ch[x][1], y), upd(x), x) : (push(y), ch[y][0] = merge(x, ch[y][0]), upd(y), y); } void split(int p, int sss, int &x, int &y) { if(!p) {x = y = 0; return;} push(p); if(sss > s[ch[p][0]]) x = p, split(ch[p][1], sss - s[ch[p][0]] - 1, ch[p][1], y); else y = p, split(ch[p][0], sss, x, ch[p][0]); upd(p); } void rotate() { int l = read(), r = read(), x, y, z; split(rt, r, y, z); split(y, l - 1, x, y); t[y] ^= 1; rt = merge(merge(x, y), z); } int main() { srand(time(0)); n = read(); m = read(); for(rei i = 1; i <= n; ++i) rt = merge(rt, New(i)); for(; m; --m) rotate(); print(rt); return 0; }
What questions can Cox ask in the commentary area and hang this burdock/kk?