AVL tree

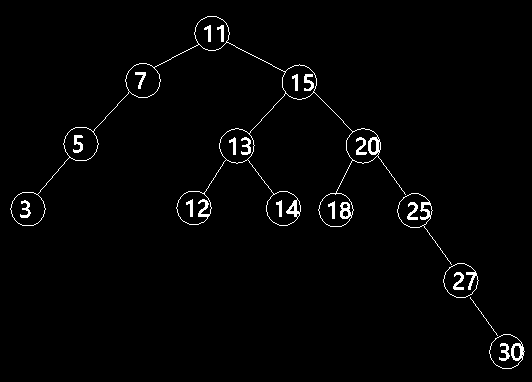
ordinary Binary Search Tree One branch may have multiple layers, while the other branches have only a few layers, as shown in Figure 1, which can lead to performance problems in adding, removing, and searching trees. Therefore, the concept of self-balanced binary tree is proposed. AVL tree (Adelson-Wells and Landis tree) is a kind of self-balanced binary tree. The height difference between the left and right subtrees of any subnode of AVL tree is not more than 1, so it is also called high-balanced tree.

Figure 1

To convert an unbalanced binary search tree into a balanced AVL tree, it is necessary to rotate the tree one or more times, which can be divided into left-handed, right-handed, left-handed and right-handed.

Left spin

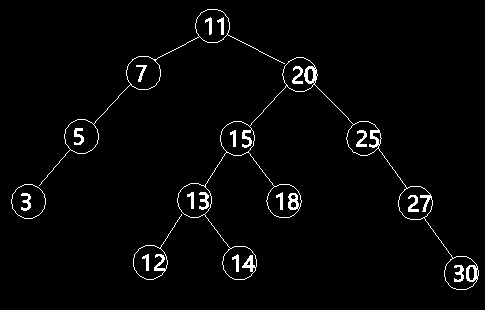
For a node B (Fig. 2), the process is equivalent to disconnecting the connection between B and parent A, connecting the right child node D of B with A, using B as the left child node of D, and E as the right child node of B. Taking the binary tree of Figure 1 as an example, the node with the key value of 15 is left-rotated. First, the connection between 15 and 11 is disconnected, then 20 and 11 are connected, 15 is the left sub-node of 20, and finally 18 is the right sub-node of 15. It can be imagined that a certain counter-clockwise rotation is made with 15 as the center. The results are shown in Figure 3.

Figure 2

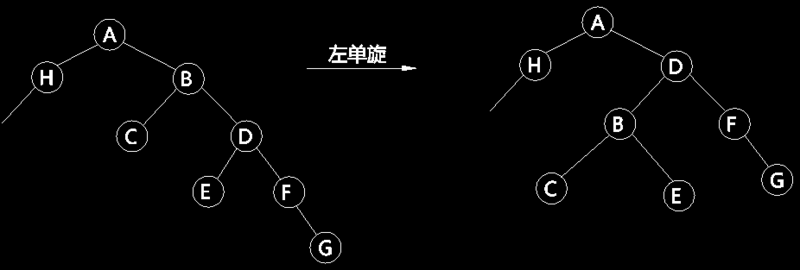
Figure 3

Looking at Figure 2 again, according to the nature of the search Binary tree, there must be D > B > A, E > B, so after rotation, it can ensure that the right child node > the parent node > the left child node, without destroying the structure of the tree.
It can be seen that a single left rotation reduces the height of the right subtree by 1, while the height of the left subtree increases by 1. The implementation code is as follows:

function roateLeft(AvlNode) {
        var node = AvlNode.right; // Save the right child node
        AvlNode.right = node.left; // The left child node of node connects to AvlNode and becomes its right child node
        node.left = AvlNode; // AvlNode connects to node to become its left child node
        return node; // Return to node and connect to the original parent of AvlNode
}

Right single rotation

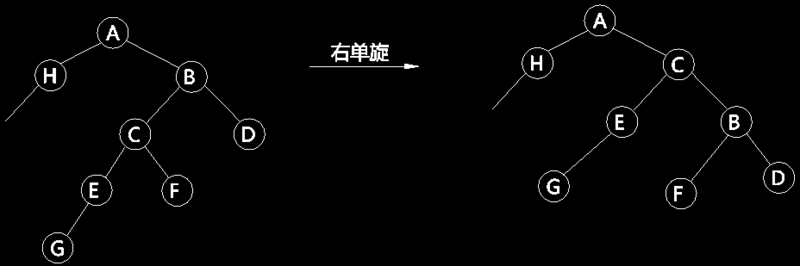
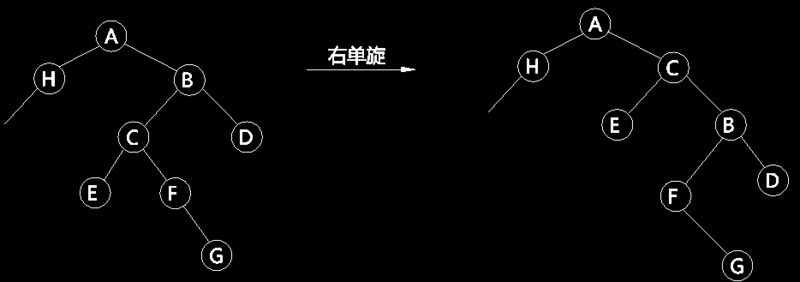
Right-handed and left-handed are similar. A node B (fig. 4) is used as right-handed. First, the connection between B and its parent A is disconnected. The left child node C and A of B are connected. The right child node F of C is regarded as the left child node of B. Similarly, because C > A, B > C > F, the tree structure will not be destroyed after rotation. It can be seen that a single right-handed rotation reduces the height of the left subtree of the node by 1, while the height of the right subtree increases by 1.

Figure 4

The implementation code is as follows:

function roateRight(AvlNode) {
        var node = AvlNode.left; // Save the left child node
        AvlNode.left = node.right; // Connect the right child node of node to AvlNode as its left child node
        node.right = AvlNode; // AvlNode connects to the node and becomes its right child
        return node; // Return node to connect to the original parent node of AvlNode
}

Left-right double rotation

In some cases, left-handed and right-handed can not achieve the goal of balanced tree. As shown in Figure 4, if B is right-handed, the height of the right subtree F of the left subtree C is less than or equal to the height of the left subtree E. Otherwise, the balance effect can not be achieved, but the imbalance is transferred from the left to the right. Figure 5 illustrates this situation. Similarly, left-handed spin has this problem.

Figure 5

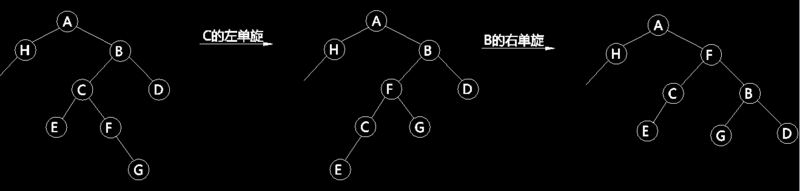
Therefore, in order to achieve this goal, it is necessary to do left single-rotation for the left sub-node of the rotating node, and then right single-rotation for the rotating node. As shown in Fig. 6, first left-handed operation is performed on the left sub-node C of node B. It can be seen that this operation is equivalent to shifting the imbalance of node C from the right to the left, thus satisfying the above conditions of right-handed rotation. Finally, right-handed operation is performed on node B to achieve the goal of balance.

Figure 6

The implementation code is as follows:

function roateLeftRight(AvlNode) {
        AvlNode.right = roateLeft(AvlNode.right); // Left single-rotation for right child node
        return roateRight(AvlNode); // Do right single spin.
}

Right-left double rotation

Similarly, as shown in Figure 2, when doing left-handed rotation for B, the height of the right subtree F of the right subtree D is greater than or equal to the height of the left subtree E, otherwise double-handed rotation is needed; that is, right-handed rotation for the right subtree D of B is done first, and then left-handed rotation for B. The implementation code is as follows:

function roateRightLeft(AvlNode) {
        AvlNode.left = roateRight(AvlNode.left); // Right-handed single-handed for left subnodes
        return roateLeft(AvlNode); // Left single rotation
}

Realizing Tree Balance

Firstly, the function of obtaining tree height is realized.

function getAvlTreeHeight(node) {
        if (node == null) {
            // node does not return 0
            return 0;
        } else {
            var leftHeight = getAvlTreeHeight(node.left);
            var rightHeight = getAvlTreeHeight(node.right);
            // Returns the maximum height in the left subtree and the right subtree
            return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
        }
}

Functions that implement a balanced tree:

function balance(node) {
    if (node == null) {
        return node;
    }
    // The height of left subtree is more than 1 higher than that of right subtree.
    if (getAvlTreeHeight(node.left) - getAvlTreeHeight(node.right) > 1) {
        if (getAvlTreeHeight(node.left.left) >= getAvlTreeHeight(node.left.right)) {
            // If the left subtree height of the left subtree is greater than or equal to the right subtree height of the left subtree
            // Direct right-handed monorotation
            node = roateRight(node);
        } else {
            // Otherwise, right-left double-turn is needed.
            node = roateRightLeft(node);
        }
        // The height of right subtree is more than 1 higher than that of left subtree.
    } else if (getAvlTreeHeight(node.right) - getAvlTreeHeight(node.left) > 1) {
        if (getAvlTreeHeight(node.right.right) >= getAvlTreeHeight(node.right.left)) {
            // If the right subtree height of the right subtree is greater than or equal to the left subtree height of the right subtree
            // Direct left monorotation
            node = roateLeft(node);
        } else {
            // Otherwise, left-right double-turn is needed.
            node = roateLeftRight(node);
        }
    }
    return node;
}

stay Binary Search Tree On the basis of this, every insertion of a node requires a tree balancing process:

var insertNode = function(node, newNode){
    if (newNode.key < node.key){
        if (node.left === null){
            node.left = newNode;
            // After inserting a node, balance the tree
            node.left = balance(node.left);
        } else {
            insertNode(node.left, newNode);
        }
    } else {
        if (node.right === null){
            node.right = newNode;
            // After inserting a node, balance the tree
            node.right = balance(node.right);
        } else {
            insertNode(node.right, newNode);
        }
    }
}

In conclusion, the principle and implementation of a self-balancing AVL tree are completed.