[introduction to GiantPandaCV] this article has been studied for a long time, and then summarized according to their own understanding steps, mainly the contents of Articles 3 and 4 of MLIR Toy Tutorials. Here we mainly explain how to customize Pass in MLIR. Here we mainly introduce various skills of defining Pass in MLIR with four examples: eliminating continuous transfer operation and Reshape operation, inline optimization Pass and shape derivation Pass. In fact, it is not difficult to understand. However, it is necessary to master these Pass implementation skills to get started with MLIR. "I maintained a project in the process of learning the compiler from scratch: https://github.com/BBuf/tvm_mlir_learn , it mainly records learning notes and some experimental codes. At present, it has obtained 150+ star. If you are interested in deep learning compiler, you can have a look. You will be more flattered if you can click star. "
preface
We have a preliminary understanding of what MLIR is, and talked about the specific process of generating MLIR from source files by Toy language, as well as the core components of MLIR, such as MLIRGen, Dialect, Operation and TableGen, and how they interact.
This note will summarize how expression morphing in MLIR is implemented based on Toy Tutorials.
Chapter3: expression deformation in MLIR (how to write Pass)
In Chapter 2, we have generated primary legal MLIR expressions, but generally, MLIR expressions can be further processed and simplified, which can be similar to the optimization of Relay IR by TVM's Pass. Here, let's take a look at how to deform the primary MLIR expression? In MLIR, expression deformation is completed based on expression matching and rewriting. This tutorial introduces the use of C + + template matching and rewriting and DRR based framework( https://mlir.llvm.org/docs/DeclarativeRewrites/ )To define expression rewriting rules, and then use the ODS framework to automatically generate code.
Optimize the Transpose operation using C + + pattern matching and rewriting
The goal here is to eliminate two Transpose sequences with mutual cancellation effect: transfer (transfer (x)) - > x, that is, there must be redundant operations for continuous transfer operations on the same input. The source code corresponding to this operation is as follows (in MLIR / test / examples / toy / CH3 / transfer_transfer. Toy):
def transpose_transpose(x) {
return transpose(transpose(x));
}
If we don't use any optimized Pass, let's see what the MLIR expression generated by the Toy source program looks like. Use the following command to generate MLIR:. / toyc-ch3.. /.. / MLIR / test / examples / Toy / CH3 / transfer_ transpose.Toy -emit=mlir.
func @transpose_transpose(%arg0: tensor<*xf64>) -> tensor<*xf64> {
%0 = toy.transpose(%arg0 : tensor<*xf64>) to tensor<*xf64>
%1 = toy.transpose(%0 : tensor<*xf64>) to tensor<*xf64>
toy.return %1 : tensor<*xf64>
}
You can see that the generated MLIR expression performs two real transfers on x and returns the Tensor after two transfers. But in fact, these two transfers are unnecessary, because the output result is actually the incoming x. Therefore, in order to optimize this situation, we first use C + + to write the code for expression matching and rewriting (in mlir/examples/toy/Ch3/mlir/ToyCombine.cpp):
/// This is an example of a c++ rewrite pattern for the TransposeOp. It
/// optimizes the following scenario: transpose(transpose(x)) -> x
struct SimplifyRedundantTranspose : public mlir::OpRewritePattern<TransposeOp> {
/// We register this pattern to match every toy.transpose in the IR.
/// The "benefit" is used by the framework to order the patterns and process
/// them in order of profitability.
SimplifyRedundantTranspose(mlir::MLIRContext *context)
: OpRewritePattern<TransposeOp>(context, /*benefit=*/1) {}
/// This method attempts to match a pattern and rewrite it. The rewriter
/// argument is the orchestrator of the sequence of rewrites. The pattern is
/// expected to interact with it to perform any changes to the IR from here.
mlir::LogicalResult
matchAndRewrite(TransposeOp op,
mlir::PatternRewriter &rewriter) const override {
// Look through the input of the current transpose.
mlir::Value transposeInput = op.getOperand();
TransposeOp transposeInputOp = transposeInput.getDefiningOp<TransposeOp>();
// Input defined by another transpose? If not, no match.
if (!transposeInputOp)
return failure();
// Otherwise, we have a redundant transpose. Use the rewriter.
rewriter.replaceOp(op, {transposeInputOp.getOperand()});
return success();
}
};
You can see that in the matchAndRewrite function, first obtain the operands of the current operation, and then judge whether the operation corresponding to the operands of the current position is transpose. If so, rewrite the expression to the operands of the inner transpose operation, otherwise there is no need to optimize and maintain the status quo.
Next, you need to register the matching rewrite pattern just created in the normalization framework so that the framework can call it. For more information on canonicalization, please see https://mlir.llvm.org/docs/Canonicalization/ , the registered code is as follows (the code is still: mlir/examples/toy/Ch3/mlir/ToyCombine.cpp):
/// Register our patterns as "canonicalization" patterns on the TransposeOp so
/// that they can be picked up by the Canonicalization framework.
void TransposeOp::getCanonicalizationPatterns(RewritePatternSet &results,
MLIRContext *context) {
results.add<SimplifyRedundantTranspose>(context);
}
After adding the expression rewriting rule to the normalization framework, we also need to modify the td file defining the Operator, enable the normalization framework, and add a new "nosideeffect" feature in defining the Operator. Now, the definition of the transfer operation is as follows:
def TransposeOp : Toy_Op<"transpose", [NoSideEffect]> {
let summary = "transpose operation";
let arguments = (ins F64Tensor:$input);
let results = (outs F64Tensor);
let assemblyFormat = [{
`(` $input `:` type($input) `)` attr-dict `to` type(results)
}];
// Enable registering canonicalization patterns with this operation.
let hasCanonicalizer = 1;
// Allow building a TransposeOp with from the input operand.
let builders = [
OpBuilder<(ins "Value":$input)>
];
// Invoke a static verify method to verify this transpose operation.
let verifier = [{ return ::verify(*this); }];
}
Finally, we need to add the optimization based on the normalization framework to the running process in the main program. This part of the code is in the dumpMLIR function in mlir/examples/toy/Ch3/toyc.cpp. As shown in the red box below:
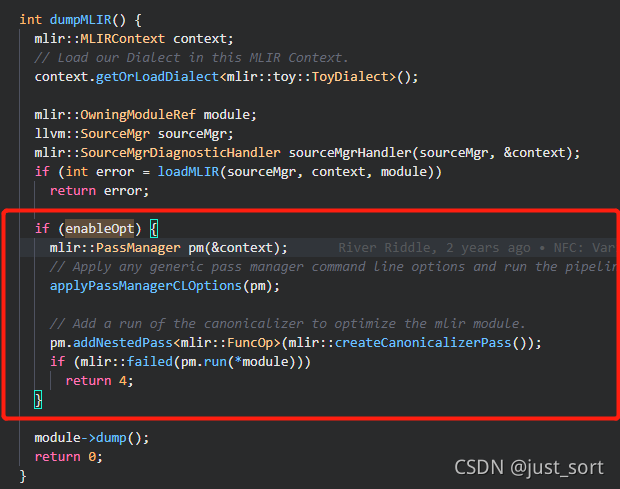
Enable optimized Pass when descending MLIR
So far, we have completed the matching and rewriting of MLIR expression based on C + +. We can use the following command to see whether the MLIR expression generated after rewriting the above transfer expression has removed the transfer. The command is:. / toyc-ch3.. /.. / MLIR / test / examples / toy / CH3 / transfer_ transpose.toy -emit=mlir -opt. The result is:
func @transpose_transpose(%arg0: tensor<*xf64>) -> tensor<*xf64> {
toy.return %arg0 : tensor<*xf64>
}
It can be seen that the optimized MLIR expression has removed the transfer operation and achieved the optimization effect.
Use DRR to optimize the tensor deformation (Reshape) operation
MLIR also provides an expression rewriting method, which automatically generates expression matching and rewriting functions based on DDR rules. The code generation part is still implemented based on ODS framework. DRR (declarative, rule-based pattern match and rewrite): declarative, rule-based pattern matching and rewriting methods. It is a DAG based declarative rewriter that provides table based pattern matching and syntax of rewriting rules.
Here, take the tensor reshape operation to eliminate redundancy in the MLIR expression as an example. The corresponding toy source file is as follows (in mlir/test/Examples/Toy/Ch3/trivial_reshape.toy):
def main() {
var a<2,1> = [1, 2];
var b<2,1> = a;
var c<2,1> = b;
print(c);
}
Use the following command to generate the corresponding MLIR expression first. See:. / toyc-ch3.. /.. / MLIR / test / examples / toy / CH3 / trial_ reshape.toy -emit=mlir
module {
func @main() {
%0 = toy.constant dense<[1.000000e+00, 2.000000e+00]> : tensor<2xf64>
%1 = toy.reshape(%0 : tensor<2xf64>) to tensor<2x1xf64>
%2 = toy.reshape(%1 : tensor<2x1xf64>) to tensor<2x1xf64>
%3 = toy.reshape(%2 : tensor<2x1xf64>) to tensor<2x1xf64>
toy.print %3 : tensor<2x1xf64>
toy.return
}
}
Obviously, the shapes and values of a, b and c are the same, and these reshape operations are redundant. Next, we will define expression matching and rewriting rules based on the DDR framework. There are several situations to consider here (the code implementation here is in mlir/examples/toy/Ch3/mlir/ToyCombine.td).
- Resolve redundant code generated by Reshape(Reshape(x)) = Reshape(x).
// Reshape(Reshape(x)) = Reshape(x)
def ReshapeReshapeOptPattern : Pat<(ReshapeOp(ReshapeOp $arg)),
(ReshapeOp $arg)>;
Replace ReshapeOp(ReshapeOp arg) with ReshapeOp arg. For many times of the same tensor deformation operation, you can perform it once.
- When the parameter of reshape and the type of the result are the same, it means that this integer operation is useless. Therefore, you can directly return the input parameter, that is, Reshape(x) = x.
// Reshape(x) = x, where input and output shapes are identical def TypesAreIdentical : Constraint<CPred<"$0.getType() == $1.getType()">>; def RedundantReshapeOptPattern : Pat< (ReshapeOp:$res $arg), (replaceWithValue $arg), [(TypesAreIdentical $res, $arg)]>;
That is, when 0.getType() is the same as 1.getType(), it is redundant, and the operand $arg is used instead.
Next, we can use the ODS framework and the defined ToyCombine.td file to automatically generate the code file ToyCombine.inc. Use the following command:
$ cd llvm-project/build
$ ./bin/mlir-tblgen --gen-rewriters ${mlir_src_root}/examples/toy/Ch3/mlir/ToyCombine.td -I ${mlir_src_root}/include/
Of course, when building a project, you can also configure the generation process in cmakelists.txt: mlir/examples/toy/Ch3/CMakeLists.txt. As follows:
set(LLVM_TARGET_DEFINITIONS mlir/ToyCombine.td) mlir_tablegen(ToyCombine.inc -gen-rewriters) add_public_tablegen_target(ToyCh3CombineIncGen)
Finally, we can execute. / toyc-ch3.. /.. / MLIR / test / examples / toy / CH3 / trial_ Reshape.toy - emit = MLIR - opt generate these Pass optimized MLIR expressions:
module {
func @main() {
%0 = toy.constant dense<[[1.000000e+00], [2.000000e+00]]> : tensor<2x1xf64>
toy.print %0 : tensor<2x1xf64>
toy.return
}
}
Chapter4: implement generalized expression conversion
In Chapter 3, we learned how to implement expression rewriting in MLIR, but there is also a very obvious problem: the Pass we implemented for Toy language can not be reused in other dialog abstractions, because here are only specific operations for some operations of Toy language. If each conversion is implemented for each dialog, it will lead to a large amount of duplicate code. Therefore, this section takes two examples to explain how to implement generalized expressions in MLIR.
This article uses the following examples (in mlir/test/Examples/Toy/Ch5/codegen.toy):
def multiply_transpose(a, b) {
return transpose(a) * transpose(b);
}
def main() {
var a<2, 3> = [[1, 2, 3], [4, 5, 6]];
var b<2, 3> = [1, 2, 3, 4, 5, 6];
var c = multiply_transpose(a, b);
var d = multiply_transpose(b, a);
print(d);
}
Let's take a look at its corresponding MLIR expression. / toyc-ch4.. /.. / MLIR / test / examples / toy / CH4 / CodeGen. Toy - emit = MLIR:
module {
func private @multiply_transpose(%arg0: tensor<*xf64>, %arg1: tensor<*xf64>) -> tensor<*xf64> {
%0 = toy.transpose(%arg0 : tensor<*xf64>) to tensor<*xf64>
%1 = toy.transpose(%arg1 : tensor<*xf64>) to tensor<*xf64>
%2 = toy.mul %0, %1 : tensor<*xf64>
toy.return %2 : tensor<*xf64>
}
func @main() {
%0 = toy.constant dense<[[1.000000e+00, 2.000000e+00, 3.000000e+00], [4.000000e+00, 5.000000e+00, 6.000000e+00]]> : tensor<2x3xf64>
%1 = toy.reshape(%0 : tensor<2x3xf64>) to tensor<2x3xf64>
%2 = toy.constant dense<[1.000000e+00, 2.000000e+00, 3.000000e+00, 4.000000e+00, 5.000000e+00, 6.000000e+00]> : tensor<6xf64>
%3 = toy.reshape(%2 : tensor<6xf64>) to tensor<2x3xf64>
%4 = toy.generic_call @multiply_transpose(%1, %3) : (tensor<2x3xf64>, tensor<2x3xf64>) -> tensor<*xf64>
%5 = toy.generic_call @multiply_transpose(%3, %1) : (tensor<2x3xf64>, tensor<2x3xf64>) -> tensor<*xf64>
toy.print %5 : tensor<*xf64>
toy.return
}
}
This is an MLIR expression without optimization. We can see that the Shape of Tensor is unknown before instantiating Tensor, that is, Tensor < * xf64 > in the expression. This will affect subsequent passes, such as Shape related passes defined in Chapter 3, resulting in inadequate optimization. Therefore, we hope to know the Shape of each Tensor before executing the Pass related to Reshape, so here we will introduce the implementation of a Shape inference Pass. In addition, an inline Pass is introduced to reduce the cost of function calls.
Inline Pass
Looking at the code above, we can find that multiply_ Small functions such as transfer are called frequently. At this time, the cost of function call itself can not be ignored. Therefore, an inline Pass is defined here, hoping to multiply_ Transfer this function becomes an inline function to improve operation efficiency.
First step
MLIR provides a general interface DialectInlinerInterface for inline processing, which contains a set of virtual hooks that can be overridden by Dialect. We need to define the inline interface and expression rewriting rules for Toy Operation based on this class. The code is implemented in: mlir/examples/toy/Ch5/mlir/Dialect.cpp:
/// This class defines the interface for handling inlining with Toy operations.
/// We simplify inherit from the base interface class and override
/// the necessary methods.
struct ToyInlinerInterface : public DialectInlinerInterface {
using DialectInlinerInterface::DialectInlinerInterface;
/// This hook checks to see if the given callable operation is legal to inline
/// into the given call. For Toy this hook can simply return true, as the Toy
/// Call operation is always inlinable.
bool isLegalToInline(Operation *call, Operation *callable,
bool wouldBeCloned) const final {
return true;
}
/// This hook checks to see if the given operation is legal to inline into the
/// given region. For Toy this hook can simply return true, as all Toy
/// operations are inlinable.
bool isLegalToInline(Operation *, Region *, bool,
BlockAndValueMapping &) const final {
return true;
}
/// This hook is called when a terminator operation has been inlined. The only
/// terminator that we have in the Toy dialect is the return
/// operation(toy.return). We handle the return by replacing the values
/// previously returned by the call operation with the operands of the
/// return.
void handleTerminator(Operation *op,
ArrayRef<Value> valuesToRepl) const final {
// Only "toy.return" needs to be handled here.
auto returnOp = cast<ReturnOp>(op);
// Replace the values directly with the return operands.
assert(returnOp.getNumOperands() == valuesToRepl.size());
for (const auto &it : llvm::enumerate(returnOp.getOperands()))
valuesToRepl[it.index()].replaceAllUsesWith(it.value());
}
};
This part of the code defines the inline interface and expression deformation rules for Toy Operation. The two isLegalToInline overloaded functions are two hooks. The first hook is used to check whether the given callable operation can be inlined into the given call is legal and whether it can be inlined. The second hook is used to check whether a given operation is legally inline to a given region. The handleTerminator function only handles toy.return, replacing the operand it.index() of the return operation with the return value it.value() (I don't know much about QAQ here).
Step 2
Next, you need to add the above expression deformation rule in the definition of Toy Dialect, which is located in mlir/examples/toy/Ch5/mlir/Dialect.cpp.
/// Dialect initialization, the instance will be owned by the context. This is
/// the point of registration of types and operations for the dialect.
void ToyDialect::initialize() {
addOperations<
#define GET_OP_LIST
#include "toy/Ops.cpp.inc"
>();
addInterfaces<ToyInlinerInterface>();
}
Addinterfaces < ToyInlinerInterface > () here is the process of registering inline Pass, where ToyInlinerInterface is the expression deformation rule defined by us.
Step 3
Next, we need to let the inline know toy.generic in IR_ Call means to call a function. MLIR provides an Operation interface CallOpInterface, which can mark an Operation as a call. To add the above operations, you need to add the line "MLIR / interfaces / callinterfaces. TD" in the definition (mlir/examples/toy/Ch5/include/toy/Ops.td) file of toy dialog.
Then add a new Operation in the dialog definition section. The code is as follows:
def GenericCallOp : Toy_Op<"generic_call",
[DeclareOpInterfaceMethods<CallOpInterface>]> {
let summary = "generic call operation";
let description = [{
Generic calls represent calls to a user defined function that needs to
be specialized for the shape of its arguments. The callee name is attached
as a symbol reference via an attribute. The arguments list must match the
arguments expected by the callee. For example:
```mlir
%4 = toy.generic_call @my_func(%1, %3)
: (tensor<2x3xf64>, tensor<2x3xf64>) -> tensor<*xf64>
```
This is only valid if a function named "my_func" exists and takes two
arguments.
}];
// The generic call operation takes a symbol reference attribute as the
// callee, and inputs for the call.
let arguments = (ins FlatSymbolRefAttr:$callee, Variadic<F64Tensor>:$inputs);
// The generic call operation returns a single value of TensorType.
let results = (outs F64Tensor);
// Specialize assembly printing and parsing using a declarative format.
let assemblyFormat = [{
$callee `(` $inputs `)` attr-dict `:` functional-type($inputs, results)
}];
// Add custom build methods for the generic call operation.
let builders = [
OpBuilder<(ins "StringRef":$callee, "ArrayRef<Value>":$arguments)>
];
}
Explanation: we use DeclareOpInterfaceMethods to declare the interface methods used in the declaration of CallOpInterface. DeclareOpInterfaceMethods this feature indicates that the program will recognize generic_ Call operation (corresponding to toy.generic_call in the original MLIR expression), and call the interface function at this location.
Then the GenericCallOp function is implemented in mlir/examples/toy/Ch5/mlir/Dialect.cpp. The code is as follows:
/// Return the callee of the generic call operation, this is required by the
/// call interface.
CallInterfaceCallable GenericCallOp::getCallableForCallee() {
return getAttrOfType<SymbolRefAttr>("callee");
}
/// Get the argument operands to the called function, this is required by the
/// call interface.
Operation::operand_range GenericCallOp::getArgOperands() { return inputs(); }
The above GenericCallOp::getCallableForCallee() {...} returns the callee of the generalized Operation. GenericCallOp::getArgOperands() {...} is used to obtain the parameter operands of the called function.
Step 4
Next, you need to add the cast operation in the dialog definition and set the interface to call. Why do I need to add a cast operation? This is because the type of input tensor is determined at the time of function call. However, when defining a function, the type of input tensor is uncertain (generalized type, which can be seen from the original version of MLIR expression above). Therefore, a hidden data type conversion is required when calling, otherwise the inline operation cannot be performed. Therefore, a cast is introduced here. The cast operation can convert the determined data type to the data type expected by the function. Next, add the cast operation in mlir/examples/toy/Ch5/include/toy/Ops.td:
def CastOp : Toy_Op<"cast", [
DeclareOpInterfaceMethods<CastOpInterface>,
DeclareOpInterfaceMethods<ShapeInferenceOpInterface>,
NoSideEffect,
SameOperandsAndResultShape
]> {
let summary = "shape cast operation";
let description = [{
The "cast" operation converts a tensor from one type to an equivalent type
without changing any data elements. The source and destination types must
both be tensor types with the same element type. If both are ranked, then
shape is required to match. The operation is invalid if converting to a
mismatching constant dimension.
}];
let arguments = (ins F64Tensor:$input);
let results = (outs F64Tensor:$output);
let assemblyFormat = "$input attr-dict `:` type($input) `to` type($output)";
}
We use DeclareOpInterfaceMethods to declare the interface methods used in the declaration of CallOpInterface. The feature DeclareOpInterfaceMethods indicates that the program will recognize the cast operation.
Next, you need to rewrite the areCastCompatible method of cast op (in mlir/examples/toy/Ch5/mlir/Dialect.cpp):
/// Returns true if the given set of input and result types are compatible with
/// this cast operation. This is required by the `CastOpInterface` to verify
/// this operation and provide other additional utilities.
bool CastOp::areCastCompatible(TypeRange inputs, TypeRange outputs) {
if (inputs.size() != 1 || outputs.size() != 1)
return false;
// The inputs must be Tensors with the same element type.
TensorType input = inputs.front().dyn_cast<TensorType>();
TensorType output = outputs.front().dyn_cast<TensorType>();
if (!input || !output || input.getElementType() != output.getElementType())
return false;
// The shape is required to match if both types are ranked.
return !input.hasRank() || !output.hasRank() || input == output;
}
This method is used to determine whether type conversion is required. If the types of inputs and outputs are compatible, return true; otherwise, type conversion (cast) is required to return false.
In addition, we also need to rewrite the hook on the ToyInlinerInterface, that is, the materializeCallConversion function:
struct ToyInlinerInterface : public DialectInlinerInterface {
....
/// Attempts to materialize a conversion for a type mismatch between a call
/// from this dialect, and a callable region. This method should generate an
/// operation that takes 'input' as the only operand, and produces a single
/// result of 'resultType'. If a conversion can not be generated, nullptr
/// should be returned.
Operation *materializeCallConversion(OpBuilder &builder, Value input,
Type resultType,
Location conversionLoc) const final {
return builder.create<CastOp>(conversionLoc, resultType, input);
}
};
This function is the entry to inline Pass.
Step 5
Add the inline Pass to the optimized pipline. In mlir/examples/toy/Ch5/toyc.cpp:
if (enableOpt) {
mlir::PassManager pm(&context);
// Apply any generic pass manager command line options and run the pipeline.
applyPassManagerCLOptions(pm);
// Inline all functions into main and then delete them.
pm.addPass(mlir::createInlinerPass());
...
}
After pm.addPass(mlir::createInlinerPass()); In this line, there is an inline Pass in the optimized pipline.
Let's see what the original MLIR expression looks like after inline optimization of Pass:
func @main() {
%0 = "toy.constant"() {value = dense<[[1.000000e+00, 2.000000e+00, 3.000000e+00], [4.000000e+00, 5.000000e+00, 6.000000e+00]]> : tensor<2x3xf64>} : () -> tensor<2x3xf64>
%1 = "toy.constant"() {value = dense<[[1.000000e+00, 2.000000e+00, 3.000000e+00], [4.000000e+00, 5.000000e+00, 6.000000e+00]]> : tensor<2x3xf64>} : () -> tensor<2x3xf64>
%2 = "toy.cast"(%1) : (tensor<2x3xf64>) -> tensor<*xf64>
%3 = "toy.cast"(%0) : (tensor<2x3xf64>) -> tensor<*xf64>
%4 = "toy.transpose"(%2) : (tensor<*xf64>) -> tensor<*xf64>
%5 = "toy.transpose"(%3) : (tensor<*xf64>) -> tensor<*xf64>
%6 = "toy.mul"(%4, %5) : (tensor<*xf64>, tensor<*xf64>) -> tensor<*xf64>
toy.print %6 : tensor<*xf64>
toy.return
}
Now the MLIR expression has only one main function, the previous transfer function has been inlined, and you can see the functions implemented by toy.cast.
Shape infer Pass
The above inline Pass implements the conversion of Tensor of determined type into Tensor of generalized type, so that the inline Operation can be completed. Next, we need to deduce the generalized Tensor shapes according to the Tensor determined by the Shape. Here, you need to use the ODS framework to generate a custom Operation interface to derive the Shape of the generalized Tensor. The whole Shape inference process will also be abstracted into a Pass like inline, acting on the MLIR expression.
Step 1: use the ODS framework to define the Shape inference Operation interface
The code is implemented in mlir/examples/toy/Ch5/include/toy/ShapeInferenceInterface.td
def ShapeInferenceOpInterface : OpInterface<"ShapeInference"> {
let description = [{
Interface to access a registered method to infer the return types for an
operation that can be used during type inference.
}];
let methods = [
InterfaceMethod<"Infer and set the output shape for the current operation.",
"void", "inferShapes">
];
}
ShapeInferenceOpInterface interface inherits OpInterface, which receives the name "ShapeInference" to be given to the generated C + + interface class as a template parameter. The description field provides a brief description of the Operation, while the methods field defines the interface method that the Operation will need to provide.
Step 2: add the feature to the necessary Toy Operation definition
Take the Mul Operation of Toy language as an example, which is implemented in mlir/examples/toy/Ch5/include/toy/Ops.td:
def MulOp : Toy_Op<"mul",
[NoSideEffect, DeclareOpInterfaceMethods<ShapeInferenceOpInterface>]> {
let summary = "element-wise multiplication operation";
let description = [{
The "mul" operation performs element-wise multiplication between two
tensors. The shapes of the tensor operands are expected to match.
}];
let arguments = (ins F64Tensor:$lhs, F64Tensor:$rhs);
let results = (outs F64Tensor);
// Specify a parser and printer method.
let parser = [{ return ::parseBinaryOp(parser, result); }];
let printer = [{ return ::printBinaryOp(p, *this); }];
// Allow building a MulOp with from the two input operands.
let builders = [
OpBuilder<(ins "Value":$lhs, "Value":$rhs)>
];
}
In the above code, declareopinterfacemethods < shapeinferenceopinterface > adds the feature of shape derivation to Mul Operation, which is similar to adding the feature of CallOpInterface to cast Operation in inline Pass.
Step 3: define the shape derivation function of the corresponding Operation
For each Operation requiring shape derivation, the corresponding inferShapes() function needs to be defined, such as Mul Operation. The resulting shape is the input shape (because it is an elementwise Operation). The code is implemented in mlir/examples/toy/Ch5/mlir/Dialect.cpp:
/// Infer the output shape of the MulOp, this is required by the shape inference
/// interface.
void MulOp::inferShapes() { getResult().setType(getOperand(0).getType()); }
Step 4: realize shape derivation Pass
This step is to introduce the specific implementation of Shape derivation Pass. The previous steps are the preconditions of this step. In this step, a Shape derivation Pass class is defined to implement the Shape inference algorithm, and a Shape inference Pass will be created based on this Pass class. The code is implemented in mlir/examples/toy/Ch5/mlir/ShapeInferencePass.cpp.
class ShapeInferencePass
: public mlir::PassWrapper<ShapeInferencePass, FunctionPass> {
public:
void runOnFunction() override {
auto f = getFunction();
// Populate the worklist with the operations that need shape inference:
// these are operations that return a dynamic shape.
llvm::SmallPtrSet<mlir::Operation *, 16> opWorklist;
f.walk([&](mlir::Operation *op) {
if (returnsDynamicShape(op))
opWorklist.insert(op);
});
// Iterate on the operations in the worklist until all operations have been
// inferred or no change happened (fix point).
while (!opWorklist.empty()) {
// Find the next operation ready for inference, that is an operation
// with all operands already resolved (non-generic).
auto nextop = llvm::find_if(opWorklist, allOperandsInferred);
if (nextop == opWorklist.end())
break;
Operation *op = *nextop;
opWorklist.erase(op);
// Ask the operation to infer its output shapes.
LLVM_DEBUG(llvm::dbgs() << "Inferring shape for: " << *op << "\n");
if (auto shapeOp = dyn_cast<ShapeInference>(op)) {
shapeOp.inferShapes();
} else {
op->emitError("unable to infer shape of operation without shape "
"inference interface");
return signalPassFailure();
}
}
// If the operation worklist isn't empty, this indicates a failure.
if (!opWorklist.empty()) {
f.emitError("Shape inference failed, ")
<< opWorklist.size() << " operations couldn't be inferred\n";
signalPassFailure();
}
}
/// A utility method that returns if the given operation has all of its
/// operands inferred.
static bool allOperandsInferred(Operation *op) {
return llvm::all_of(op->getOperandTypes(), [](Type operandType) {
return operandType.isa<RankedTensorType>();
});
}
/// A utility method that returns if the given operation has a dynamically
/// shaped result.
static bool returnsDynamicShape(Operation *op) {
return llvm::any_of(op->getResultTypes(), [](Type resultType) {
return !resultType.isa<RankedTensorType>();
});
}
};
} // end anonymous namespace
/// Create a Shape Inference pass.
std::unique_ptr<mlir::Pass> mlir::toy::createShapeInferencePass() {
return std::make_unique<ShapeInferencePass>();
}
ShapeInferencePass inherits FunctionPass and rewrites its runOnFunction() interface to implement shape inference algorithm. First, a list of operations whose output return value is generalized tensor will be created, and then the operator of tensor whose type is determined when traversing the list to find the input operand. If the exit loop is not found, otherwise, the Operation will be deleted from the loop and the corresponding inferShape() function will be called to infer that the output of the Operation will return to Tensor's shape. If the Operation list is empty, the algorithm ends.
Step 5: add the shape derivation Pass to the optimized pipline
Similar to inline Pass, you need to add the shape derivation Pass to the optimized pipline. The above inline Pass has been shown, and the code will not be pasted again.
So far, we have completed the implementation of inline Pass and shape derivation Pass. Let's see what the MLIR expression looks like after these two Pass optimizations. Execute. / toyc-ch4.. /.. / MLIR / test / examples / toy / CH4 / CodeGen. Toy - emit = MLIR - opt to obtain the optimized MLIR expression:
module {
func @main() {
%0 = toy.constant dense<[[1.000000e+00, 2.000000e+00, 3.000000e+00], [4.000000e+00, 5.000000e+00, 6.000000e+00]]> : tensor<2x3xf64>
%1 = toy.transpose(%0 : tensor<2x3xf64>) to tensor<3x2xf64>
%2 = toy.mul %1, %1 : tensor<3x2xf64>
toy.print %2 : tensor<3x2xf64>
toy.return
}
}
Reference articles
- https://zhuanlan.zhihu.com/p/106472878
- https://www.zhihu.com/people/CHUNerr/posts
- https://mlir.llvm.org/docs/Tutorials/Toy/Ch-4/