Polynomial evaluation
For polynomials f ( x ) = a 0 + a 1 ∗ x 1 + a 2 ∗ x 2 + . . . + a n − 1 ∗ x n − 1 f(x)=a_{0}+a_{1}*x^{1}+a_{2}*x^{2}+...+a_{n-1}*x^{n-1} f(x)=a0 + a1 * x1+a2 * x2+...+an − 1 * xn − 1 we usually spend O ( n 2 ) O(n^2) O(n2) n n Value at n points. The FFT proposed by Cooley and Tukey in 1965 can be used in O ( n l o g n ) O(nlogn) The time of O(nlogn) is obtained n n Value at n points. Its essence is to eliminate the computational redundancy by using the periodicity of complex numbers and divide and conquer algorithm. Therefore, when accelerating FFT evaluation, only the value at special points can be calculated, such as 1 , w , w 2 , . . . , w n − 1 1,w,w^2,...,w^{n-1} 1,w,w2,...,wn − 1, where w = e 2 π ∗ i / n w=e^{2\pi*i/n} w=e2π∗i/n
The specific process is not deduced here. The pseudo code for calculating polynomial value by FFT is given directly.

– PPT with reference to divination

Find polynomial
So if you know n n How to find the value of n points f ( x ) f(x) What about f(x)? Firstly, the matrix form of finding the value of polynomial is given. (originally, I wanted to write in Latex. I was lazy and just took a screenshot)

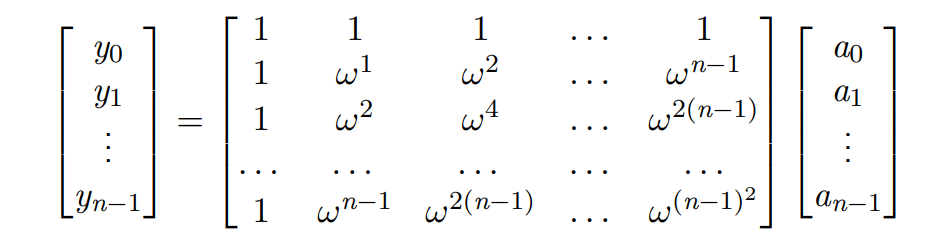
Through the matrix form, it is obvious that we know n n When the values of n points are, the coefficients of the polynomial can be obtained by calculating the inverse left multiplication of the matrix by the value of the polynomial. Usually, Gauss elimination is used to solve the inverse of the matrix O ( n 3 ) O(n^3) Time of O(n3). However, if it is a finger at a specific point, the inverse matrix can be obtained directly through the properties of the complex number. At the same time, using the periodicity of the complex number and the divide and conquer algorithm, similar to FFT, it can O ( n l o g n ) O(nlogn) The coefficients of polynomials are obtained in the time of O(nlogn).

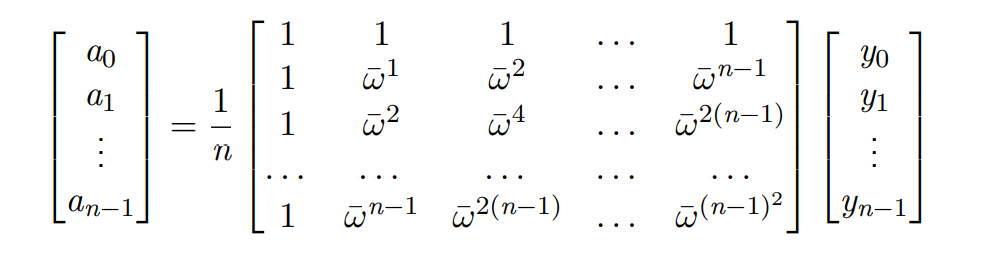
Therefore, you only need to modify the FFT code slightly.

Polynomial multiplication
For polynomials A ( x ) A(x) A(x) and B ( x ) B(x) B(x) C ( x ) C(x) C(x)
A ( x ) = a 0 + a 1 ∗ x 1 + a 2 ∗ x 2 + . . . + a n − 1 ∗ x n − 1 B ( x ) = b 0 + b 1 ∗ x 1 + b 2 ∗ x 2 + . . . + b n − 1 ∗ x n − 1 C ( x ) = A ( x ) ∗ B ( x ) = c 0 + c 1 ∗ c 1 + c 2 ∗ x 2 + . . . + c 2 n − 2 ∗ x 2 n − 2 A(x)=a_{0}+a_{1}*x^{1}+a_{2}*x^{2}+...+a_{n-1}*x^{n-1} \\ B(x)=b_{0}+b_{1}*x^{1}+b_{2}*x^{2}+...+b_{n-1}*x^{n-1} \\ C(x)=A(x)*B(x)=c_{0}+c_{1}*c^{1}+c_{2}*x^{2}+...+c_{2n-2}*x^{2n-2} A(x)=a0​+a1​∗x1+a2​∗x2+...+an−1​∗xn−1B(x)=b0​+b1​∗x1+b2​∗x2+...+bn−1​∗xn−1C(x)=A(x)∗B(x)=c0​+c1​∗c1+c2​∗x2+...+c2n−2​∗x2n−2
c k = c_{k}= Each term of ck = is actually calculating convolution, and the time required to find C is O ( n 2 ) O(n^2) O(n2). At this time, a classic picture will be put on.

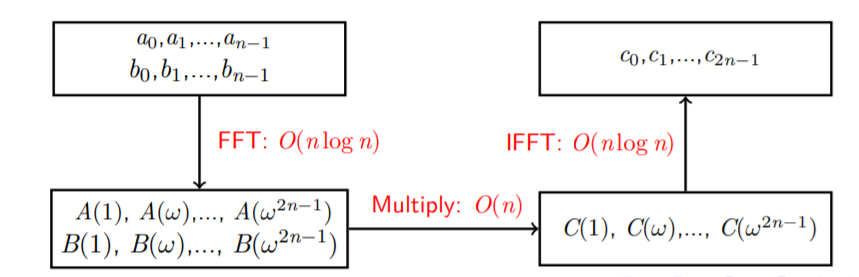
From the above logic, we first calculate the value at the specific point through FFT to obtain the value of polynomial C at the specific point, and then obtain the coefficient of C through IFFT. In fact, in essence, the process of finding C from A*B is the process of convolution, and we can accelerate the process of convolution through FFT. The process on the figure is actually converted to the frequency domain for calculation through FFT. In fact, FFT is to find the value in the frequency domain in the signal field, but in the current algorithm, it is not necessary to think about the time domain and frequency domain for the time being.
Give a problem of finding polynomial product with FFT. Luogu P3803, FFT template question. Portal

#include <bits/stdc++.h>
using namespace std;
const double PI = acos(-1);
const int MAX = 4e6 + 10;
struct Complex{
    double x, y;
    Complex(){x=y=0;}
    Complex(double x,double y){
        this->x = x;
        this->y = y;
    }
}a[MAX], b[MAX];
Complex operator+(Complex a, Complex b) { return Complex(a.x + b.x, a.y + b.y); }
Complex operator-(Complex a, Complex b) { return Complex(a.x - b.x, a.y - b.y); }
Complex operator*(Complex a, Complex b) { return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }

void fft(int n,Complex * a){
    if(n<=1)
        return ;
    int mid = n >> 1;
    Complex a1[mid], a2[mid];
    for (int i = 0; i < mid;i++){
        a1[i] = a[i << 1];
        a2[i] = a[(i << 1) + 1];
    }
    fft(mid, a1);
    fft(mid, a2);
    Complex w1(cos(PI/mid),sin(PI/mid)),w(1,0),x;
    for (int i = 0; i < mid;i++){
        x = w * a2[i];
        a[i] = a1[i] + x;
        a[i + mid] = a1[i] - x;
        w =w* w1;
    }
}
void ifft(int n,Complex * a){
    if(n<=1)
        return ;
    int mid = n >> 1;
    Complex a1[mid], a2[mid];
    for (int i = 0; i < mid;i++){
        a1[i] = a[i << 1];
        a2[i] = a[(i<<1) + 1];
    }
    ifft(mid, a1);
    ifft(mid, a2);
    Complex w1(cos(PI/mid),-sin(PI/mid)),w(1,0),x;
    for (int i = 0; i < mid;i++){
        x = w * a2[i];
        a[i] = a1[i] + x;
        a[i + mid] = a1[i] -x;
        w =w*w1;
    }
    
}
int main(){
    int n, m;
    cin >> n >> m;
    for (int i = 0; i <=n;i++){
        cin >> a[i].x;
    }
    for (int i = 0; i <=m;i++){
        cin >> b[i].x;
    }
    int k = 1;
    while(k<=n+m)
        k <<= 1;
    fft(k, a);
    fft(k, b);
    for (int i = 0; i <= k; i++){
        a[i] = a[i] * b[i];
    }
    ifft(k, a);
    for (int i = 0; i <=(n+m);i++){
        cout << int(a[i].x / k + 0.5) <<" ";
    }
    //system("pause");
    return 0;
}

To give my solution is actually to write it according to the pseudo code given above.

Large integer multiplication
How to use FFT to calculate the multiplication of large integers? In fact, a polynomial can be regarded as a long integer when x = 10 x=10 x=10 is brought into the polynomial, and the coefficient of the polynomial is the digit of the long integer, so it can be calculated and solved by using the multiplication of the polynomial and FFT. A picture posted here can quickly understand the process. The content of the picture is quoted from - dada

Here is an example of Leetcode: Portal , use FFT to calculate the multiplication of large integers. The following is the solution to the problem.

class Solution {
    struct Complex{
    double x, y;
    Complex(){x=y=0;}
    Complex(double x,double y){
        this->x = x;
        this->y = y;
    }
}a[1000], b[1000];
public:
    const double PI = acos(-1);
friend Complex operator+(Complex a, Complex b) { return Complex(a.x + b.x, a.y + b.y); }
friend Complex operator-(Complex a, Complex b) { return Complex(a.x - b.x, a.y - b.y); }
friend Complex operator*(Complex a, Complex b) { return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }
    void fft(int n,Complex * a){
    if(n<=1)
        return ;
    int mid = n >> 1;
    Complex a1[mid], a2[mid];
    for (int i = 0; i < mid;i++){
        a1[i] = a[i << 1];
        a2[i] = a[(i << 1) + 1];
    }
    fft(mid, a1);
    fft(mid, a2);
    Complex w1(cos(PI/mid),sin(PI/mid)),w(1,0),x;
    for (int i = 0; i < mid;i++){
        x = w * a2[i];
        a[i] = a1[i] + x;
        a[i + mid] = a1[i] - x;
        w =w* w1;
    }
}
    void ifft(int n,Complex * a){
    if(n<=1)
        return ;
    int mid = n >> 1;
    Complex a1[mid], a2[mid];
    for (int i = 0; i < mid;i++){
        a1[i] = a[i << 1];
        a2[i] = a[(i<<1) + 1];
    }
    ifft(mid, a1);
    ifft(mid, a2);
    Complex w1(cos(PI/mid),-sin(PI/mid)),w(1,0),x;
    for (int i = 0; i < mid;i++){
        x = w * a2[i];
        a[i] = a1[i] + x;
        a[i + mid] = a1[i] -x;
        w =w*w1;
    } 
    }
    string multiply(string num1, string num2) {
        if(num1=="0"||num2=="0") return "0";
        int n =num1.size();int m = num2.size();
        for(int i=0;i<n;i++){
            a[i].x=num1[i]-'0';
        }
        for(int i=0;i<m;i++){
            b[i].x=num2[i]-'0';
        }
        int k=1;
        while(k<=(n+m)) k<<=1;
        fft(k,a);
        fft(k,b);
        for(int i=0;i<=k;i++){
            a[i]=a[i]*b[i];
        }
        ifft(k,a);
        //Handle carry
        string ans="";
        int flag=0;
        vector<int>as;
        n--,m--;
        for(int i=(n+m);i>=0;i--){
        as.push_back(int(a[i].x/k+0.5));
        }
        for(auto x :as){
            ans+=to_string((x+flag)%10);
            flag=(x+flag)/10;
        }
        if(flag){
            ans+=to_string(flag);
        }
        //Remove leading 0
        /*for(int i=0;i<ans.size();i++){
            if(ans[i]=='0'){
                ans=ans.substr(0,i)+ans.substr(i+1);
                i--;
            }
            else break;
        }*/
        reverse(ans.begin(),ans.end());
        
        return ans;
    }
};

In fact, you can directly use the FFT template for polynomial above, but you still encounter many pits when writing this question. Pay attention to details!

In fact, the essence of FFT acceleration is the use of divide and conquer algorithm. You can refer to Mr. Bu Dongbo's explanation, which is easy to understand and refreshing. The recording and broadcasting class can be found on station b.

As a digression, the divination operator class is really good. There are some points I didn't understand before, which suddenly impressed me. If only I could hear his algorithm class in my undergraduate course. At the same time, I recalled the last question of the freshman ACM school competition, that is, using FFT to calculate the multiplication of large integers. At the same time, I remembered an FFT template question of the ACM provincial competition that year, and the days when I was abused by communication principle and digital signal processing. I was really filled with emotion.