L2 - Fundamentals of data structures - Lesson 07 - Dynamic Arrays
Original gourd teacher Yunfan youpei 2020-12-19 13:34
L2 - Fundamentals of data structures - Lesson 07 - Dynamic Arrays
Variable length array
cin >> n; int a[n];
Strictly speaking, the above code is not supported by c + + standard, although most compilers can compile it
c + + is a superset of c, but it does not support variable length arrays because c + + provides a more powerful dynamic array vector
In the information science competition, some topics need to define large arrays, which will lead to the error of "exceeding the memory limit". For example, if there are too many vertices in a graph, the use of adjacency matrix will exceed the memory limit. It is easy to make mistakes when using pointers to implement adjacency table, and the use of vector is concise and convenient, which can also save storage space.
vector
vector is a dynamic array that can hold many types of data, so it is also called a container
vector header file
#include <vector>
vector initialization
template <class T>
The angle brackets here are not the greater than sign or the less than sign. The "type formal parameters" are placed inside. Pay special attention to adding spaces in this angle bracket, otherwise it may become > > or < <
For example:
vector <vector<int> > mp // There must be a space between two > > vector <int> a; //Generate a vector named a that holds an int object vector <string> b; //Generate a vector named b that holds the string object vector <vector<int> > mp; //Generate a vector that holds vector type variables
Mode 1 given size
vector<int> a(10); //Defines a vector with 10 integer elements (angle brackets are the element type name, which can be any legal data type), does not have an initial value, and its value is uncertain
Mode 2 given size and initial value
vector<int> a(10, 1); //Define a vector with 10 integer elements, and the given initial value of each element is 1
Mode 3 initialization with vector / array
vector<int> a(b);
//Assign a value to vector a with vector b, and the value of a is completely equivalent to the value of b
vector<int> a(b.begin(), b.begin+3);
//Assign the element from 0-2 (of three) in vector b to a, and the type of a is int
int b[7]={1,2,3,4,5,6,7};
vector<int> a(b, b+7);
//Get initial value from array
The differences and similarities between arrays and vectors are shown in the following table
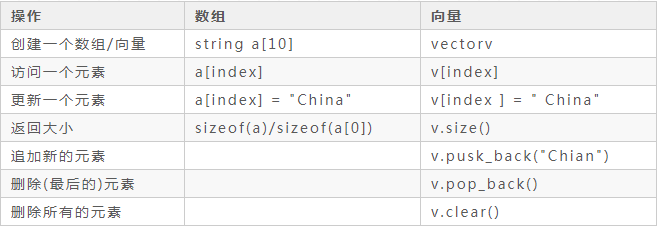
vector is a dynamic array that allocates memory in the heap
Like an array, a vector is a continuous memory space allocated, and the starting address is unchanged, so it can well support random access, with a complexity of O(1). However, when inserting and deleting in the head or in the middle, it will involve the movement of elements, that is, the copy of memory blocks, so the complexity of inserting or deleting elements in the middle is O(n) The operation on the last element is the fastest (adding and deleting elements later is the fastest), and there is generally no need to move memory at this time.
Several important operations of vector object
#include<vector> vector<int> a, b; //b is a vector, and 0-2 elements of b are assigned to vector a a.assign(b.begin(), b.begin() + 3); //A contains four elements with a value of 2 a.assign(4, 2); //Returns the last element of a a.back(); //Returns the first element of a a.front(); //Returns the ith element of a if and only if a exists a[i]; //Empty elements in a a.clear(); //Judge whether a is empty. If it is empty, it returns true. If it is not empty, it returns false a.empty(); //Deletes the last element of the a vector a.pop_back(); //Delete the first (from the 0) to the second element in a, that is, the deleted element starts from a.begin()+1 (including it) to a.begin()+3 (excluding it) a.erase(a.begin()+1, a.begin()+3); //Insert an element after the last vector of a with a value of 5 a.push_back(5); //Insert the value 5 at the position of the first element of a (calculated from the 0th), a.insert(a.begin()+1, 5); //Insert 3 numbers at the position of the first element of a (calculated from the 0), and their values are all 5 a.insert(a.begin()+1, 3, 5); //b is an array. Insert the third element of b to the fifth element (excluding b+6) at the position of the first element of a (calculated from the 0th element) a.insert(a.begin()+1, b+3, b+6); //Returns the number of elements in a a.size(); //Returns the total number of elements a can hold in memory a.capacity(); //Adjust the number of existing elements of a to 10, delete more and supplement less, and its value is random a.resize(10); //Adjust the number of existing elements of a to 10, delete more and supplement less, and its value is 2 a.resize(10, 2); //Expand the capacity of a to 100, a.reserve(100); //b is a vector, and the elements in a and b are exchanged as a whole a.swap(b); //b is the vector, and the vector comparison operation is also! = > = > < =< a==b;
Several ways to access vector sequentially
Add an element to vector a
vector<int> a;
for(int i = 0; i < 10; i++) {
a.push_back(i);
}
Obtained by subscript
int a[6]={1,2,3,4,5,6};
vector<int> b(a,a+4);
for(int i = 0; i <= b.size() - 1; i++) {
cout << b[i] << endl;
}
Read by iterator
int a[6] = {1, 2, 3, 4, 5, 6};
vector<int> b(a, a+4);
vector<int>::iterator it;
for( it = b.begin(); it != b.end(); it++) {
cout<< *it << " ";
}
Several important algorithms
#include <algorithm> //Arrange the elements in a from a.begin() (including it) to a.end() (excluding it) from small to large sort(a.begin(), a.end()); //Invert the elements from a.begin() (including it) to a.end() (excluding it) in a, but do not arrange them. For example, the elements in a are 1,3,2,4, and the inverted elements are 4,2,3,1 reverse(a.begin(), a.end()); //Copy the elements from a.begin() (including it) to a.end() (excluding it) in a to B, copy from the position of b.begin()+1 (including it), and overwrite the original elements copy(a.begin(), a.end(), b.begin()+1); //Find 10 in the elements from a.begin() (including it) to a.end() (excluding it) in a, and return its position in the vector if it exists find(a.begin(), a.end(), 10);
Initialize 2D vector
// Initialize a two-dimensional matrix, row M, column N, and the value is 0
vector<vector<int> > matrix(M, vector<int>(N));
//Equivalent to the following
vector<vector<int> > matrix(M);
for(int i=0;i<M;i++) {
matrix[i].resize(N);
}
//Equivalent to the following
vector< vector<int> > matrix;
matrix.resize(M);//Line M
for(int i=0;i<matrix.size();i++){
matrix[i].resize(N);//Each row is an N column
}
// Initialize a two-dimensional matrix with row M and column N, and the value is customized as data;
vector<vector<int>> matrix(M, vector<int>(N,data));
Learn to initialize a two-dimensional array with braces
vector<vector<int>> matrix1{};
vector<vector<int>> matrix2{ {1}, {1, 1} };//Learn to initialize a two-dimensional array with braces
matrix1.push_back({ 1, 2, 1 });//insert
Initialize a two-dimensional vector with row M and column unfixed
vector<vector> matrix(M); //M rows, the number of columns is not fixed
int col;
vector<int> temp;
for(int i = 0; i < M; i++){
cout << "please input the col of "<<i<<" row" << endl;
cin >> col;//Determine the number of columns in row i
cout << i << " row has "<< col << " col " << " please input these " << endl;
for(int j = 0; j < col; j++{
int data;
cin >> data;
temp.push_back(data);
}
matrix[i] = temp;
temp.clear();
}
Initialize a two-dimensional vector. The rows and columns are not fixed
#include <iostream>
#include<vector>
using namespace std;
int main()
{
vector<vector<int>> matrix;//The number of rows and columns is not fixed
cout << "please input rows of matrix: " << endl;
int rows;
cin >> rows;
matrix.resize(rows);
int col;
vector<int> temp;
for (int i = 0; i < rows; i++) {
cout << "please input the cols of " << i << "th row" << endl;
cin >> col;//Determine the number of columns in row i
cout << i << "th row has " << col << " cols," << "please input these" << endl;
for (int j = 0; j < col; j++){
int data;
cin >> data;
temp.push_back(data);
}
matrix[i] = temp;
temp.clear();
}
cout << "output matrix:" << endl;
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[i].size(); j++) {
cout << matrix[i][j] << " ";
}
cout << endl;
}
cout << endl;
return 0;
}
Example parcel cabinet
P3613 [deep foundation 15. Example 2] parcel cabinet
Title Description
There is a parcel cabinet in the supermarket. Each parcel cabinet has a different number of grids. The i-th parcel cabinet has a grid, but we don't know the value of each grid. For each parcel cabinet, the grid number starts from 1 to. Now there are operations:
1 i j k: store items in the j-th grid of the i-th cabinet. When k=0, it means to empty the grid.
2 i j: query the items in the j-th grid of the i-th cabinet to ensure that there are things stored in the queried cabinet.
It is known that there will be no more than bag sending grids in the supermarket. It is certain but unknown, but it must not be less than the maximum grid number requested for storing items in this cabinet. Of course, there may be no grid in some bag sending cabinets.
Input format
The first line contains two integers n and q, the number of parcel cabinets and the number of inquiries.
The next q integers represent an operation.
Output format
For query operations, the answer is output.
Input and output samples
input
5 4 1 3 10000 114514 1 1 1 1 2 3 10000 2 1 1
output
114514 1
analysis
The memory limit is 125M. The number of int types that can be stored is 125 * 1024 * 1024 / 4 = 32768000. Therefore, a grid can be stored
However, there are two parcel lockers, each with a grid. If you define a two-dimensional array, you will need an int, so MLE
Then use vector
We still don't know how many grids there are in each cabinet, so we need to record two quantities, one is the grid number, and the other is the items in the grid. First find the number, and then find the items under the number
Reference answer
#include <iostream>
#include <vector>
using namespace std;
const int N = 100005;
vector <int> a[N];
vector <int> idx[N];
int n, q;
int main()
{
cin >> n >> q;
while(q--) {
int opt, i, j, k;
cin>>opt;
if(opt == 1) {
cin >> i >> j >> k;
idx[i].push_back(j);
a[i].push_back(k);
}
else {
cin >> i >> j;
for(int id = a[i].size() - 1; i >= 0; id--) {
if(idx[i][id] == j) {
cout<<a[i][id]<<endl;
break;
}
}
}
}
return 0;
}
Example chores
P1113 miscellaneous
Title Description
John's farm has a lot of chores to complete before milking the cows. Each chore takes a certain amount of time to complete it. For example, they have to gather the cows, drive them into the barn, wash their breasts and do some other work. It is necessary to finish all the chores as soon as possible, because there is more time to squeeze out more milk. Of course, some chores can only be carried out when others are completed. For example, only when the cow is driven into the cowshed can it start to wash its breasts, and the cow can't be milked before washing its breasts. We call these work preparations for completing this work. At least one chore does not require preparation. The work that can be completed as early as possible is marked as chore 1. John has a list of n chores to be completed, and this list is in a certain order. The preparation of chores K (k > 1) can only be in chores 1 to K − 1.
Write a program to read the job description of each chore from 1 to n. Calculate the shortest time for all chores to be completed. Of course, unrelated chores can work at the same time, and you can assume that John's farm has enough workers to complete any number of tasks at the same time.
Input format
Line 1: an integer n, the number of chores that must be completed (3 ≤ n ≤ 10000);
Lines 2 to (n+1): there are n lines in total, and each line has some integers separated by 1 space, which respectively represent:
Work serial number (1 to n, orderly in the input file);
Time required to complete the work len(1 ≤ len ≤ 100);
Some preparations that must be completed, with a total of no more than 100, are ended by a number of 0. Some chores have no work to prepare, only describe a separate 0, and there will be no redundant spaces in the whole input file.
Output format
An integer representing the minimum time required to complete all chores.
Input and output samples
Enter #1 copy
7 1 5 0 2 2 1 0 3 3 2 0 4 6 1 0 5 1 2 4 0 6 8 2 4 0 7 4 3 5 6 0
Output #1 copy
23
analysis
This problem is a little more complicated. For modeling, each task has several prerequisite tasks. After these tasks are completed, the task can be completed. We can use vector
Reference code
#include <bits/stdc++.h>
using namespace std;
int n;
struct task {
int len;
vector<int> kl;
};
task k[10001];
int maxlen, len;
int main()
{
int i, p;
scanf("%d", &n);
for(i = 1; i <= n; i++) {
scanf("%d %d", &p, &k[i].len);
while(true) {
scanf("%d",&p);
if(p == 0)
break;
k[i].kl.push_back(p);
}
}
for(i = 1; i <= n; i++) {
len = 0;
for(int j = 0; j < k[i].kl.size(); j++) {
len = max(len, k[k[i].kl[j]].len);
}
k[i].len += len;
maxlen = max(k[i].len, maxlen);
}
printf("%d", maxlen);
return 0;
}