
Introduction
It's a headache to have lunch in the canteen at noon. The way to the canteen is always in a hurry. Why? It's worth saying that if you go later, you'll know what it's called a sea of people. When you line up in the canteen, compared with the students, there are only a few aunts playing rice. When there are people at each window, we have to wait until the front. One of our students left after dinner. The people in the line behind could go on until it was their turn. It's not hard. But the order and rules should be obeyed by all of us. We can only complain about our late arrival.
This "first in, first out" example is one of the basic data structures we call "queues."“
When using the computer, sometimes the machine will be in the state of suspected crash, the mouse point seems to be useless, double clicking any shortcut does not move, just when you lose patience and plan to reset, suddenly it is like waking up after drinking, and all the operations you just clicked are executed in order, which is actually because there are many operations in the operating system Program hidden needs to be output through a channel, and it is caused by queuing in order -- datastructure of Dahua
Basic definition of queue
Definition: a queue is a linear table that only allows deletion on one segment and insertion on the other.
The segment allowed to be inserted is called rear, and the one allowed to be deleted is called front.
The data element of a queue is also called queue element. Inserting a queue element into a queue is called queue in, and deleting a queue element from a queue is called queue out. That's because the queue can only be inserted in one segment and deleted at the other end, so this is the concept of FIFO first in first out shown in our previous example.
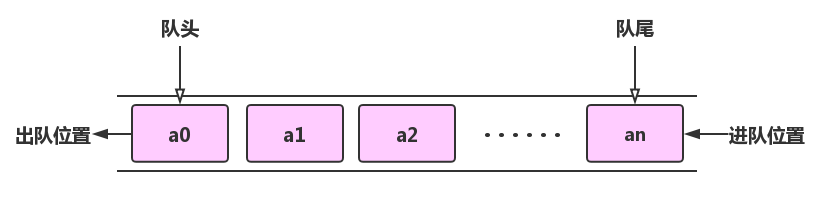
Add: in addition, there are also queues called double end queues, that is, linear tables that can insert and delete operations on both sides of the table
Two terminal queue classification:
-
Output limited two terminal queue: delete operation is limited to one segment of the table, while insert operation is allowed to both ends of the early table
-
Insert operations are limited to one segment of the table, while delete operations are allowed to occur at both ends of the table
Abstract data type of the queue
#ifndef _QUEUE_H_ #define _QUEUE_H_ #include <exception> using namespace std; // Used to check the validity of the scope class outOfRange:public exception { public: const char* what()const throw() { return "ERROR! OUT OF RANGE.\n"; } }; // Used to check the validity of the length class badSize:public exception { public: const char* what()const throw() { return "ERROR! BAD SIZE.\n"; } }; template <class T> class Queue { public: //Judge team empty virtual bool empty() const = 0; //Clear queue virtual void clear() = 0; //Find queue length virtual int size() const = 0; //Join the team virtual void enQueue(const T &x) = 0; //Team out virtual T deQueue() = 0; //Reading team leader element virtual T getHead() const = 0; //virtual destructor virtual ~Queue(){} }; #endif
Circular queue
As a special linear table, queues naturally have two ways: sequential storage and chained storage. Let's take a look at its sequential storage -- circular queue.
In the sequential storage of queues, in addition to creating an array space with a certain space, we also need two pointers, pointing to the front end and the micro end of the queue. In the following code, we choose to point the queue head pointer to the previous position of the head element, and the queue tail pointer to the queue tail element (of course, this is not the only way, we can also point the head pointer to the head element, the queue The tail pointer points to the next position of the tail element, and the principle is basically the same.)
Why do we do this, and why is this storage called circular queues?
Let's analyze step by step:
First, we draw the process of queue elements entering and leaving the team according to our general idea, for example, queue elements leaving the team.
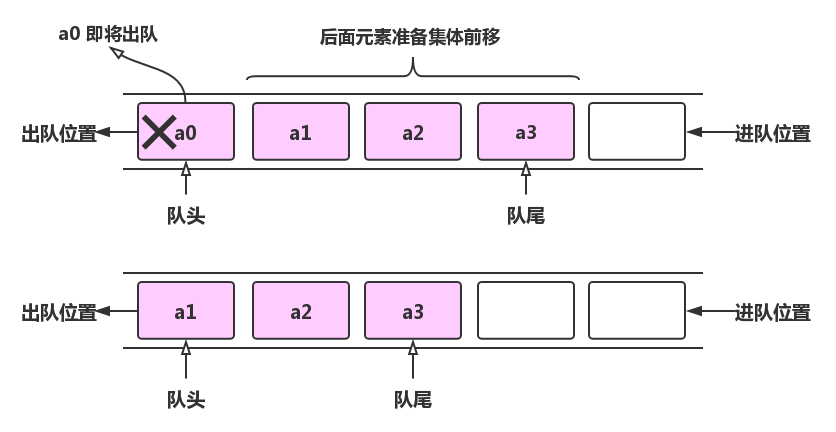
Such an assumption is drawn according to the example of canteen queuing in front of us, but we can clearly see that when a0 is out of the queue, all elements after a0 need to move forward and fill in the vacancy, but we pay attention to the word "performance" in the computer, how can we improve the performance of the queue?
So the circular queue is designed. If we don't restrict the queue head to the front of the whole space, our elements won't need to move collectively.

Question 1
At this time, we need to consider such issues:
(1) how to solve the problem of overlapping team head and team tail when there is only one element?
- At this time, the two pointers we mentioned above are useful (the team head pointer points to the previous position of the head element, and the team tail pointer points to the team tail element). When the head tail pointers are equal, it means the empty queue.
Question two
But there is a big problem!
If there is free space in front of us, we can say that once there is no space in front of the head element, our team head pointer will point out of the array, and the array will cross the boundary. What should we do?
We can see that although there is no space in our meter head, there is still free space in the second half of the meter. This phenomenon is called false overflow. For example, when approaching the class, you walk into the classroom slowly and see that there are only two positions left in the front row. You will not turn around and go. Of course, you can go to the front row to sit. Only when there are no seats, you can consider leaving.
We can make such a feasible plan
- We just need to connect the end of this queue. When the space behind is full, then we can enter the queue from the space out of the front. Similarly, our header pointer also finds the position to point to.
- The specific connection method is to consider unit 0 of date[0...maxSize] as maxSize - 1.
Question three
We just mentioned that when the header pointer and the footer pointer are equal, the empty queue is solved. But when the table is full, you will find that the header and footer pointer are equal, too. So how to solve this problem? (we offer three possible solutions)
- A: set a flag variable flag. When front = rear, and flag = 0, it is empty. If flag = 1, it means the queue is full.
- B: design a counter count to count the number of elements in the current queue, count == 0 the queue is empty, count = = maxsize the queue is full
- C: reserve a storage space to distinguish whether the queue is full, that is to say, when a cell is still idle, we think the table is full.
Let's focus on the methods in C
According to this method, we can sum up the expressions of several conditions.
-
Conditions for full queue: (rear + 1)% maxsize = = front
-
The condition that the queue is empty: front == rear
-
Number of elements in the queue: (Rear - front + maxsize)% maxsize
-
Team entry: rear = (rear + 1)% maxsize
-
Outbound: front = (front + 1)% maxsize
(I) type definition of sequence queue
#ifndef _SEQQUEUE_H_ #define _SEQQUEUE_H_ #include "Queue.h" template <class T> class seqQueue:public Queue<T> { private: //Array to hold elements T &data; //Size of the queue int maxSize; //Define team head and tail pointers int front, rear; //Expand queue space void resize(); public: seqQueue(int initSize = 100); ~seqQueue() {delete []data;} //Clear queue void clear() {front = rear = -1;} //Sentence blank bool empty() const {return front == rear;} //Sentence full bool full() const {return (rear + 1) % maxSize == front;} //queue length int size() const {(rear- front + maxSize) % maxSize;} //Join the team void enQueue(const T &x); //Team out T deQueue(); //Team leader element T getHead() const; }; #endif
(II) initialize an empty queue
template <class T> seqQueue<T>::seqQueue(int initSize) { if (initSize <= 0) throw badSize(); data = new T[initSize]; maxSize = initSize; front = rear = -1; }
(three) join the team
template <class T> void seqQueue<T>::enQueue(const T &x) { //Capacity expansion when the team is full if ((rear + 1) % maxSize == front) resize(); //Move tail pointer rear = (rear + 1) % maxSize; //x team entry data[rear] = x; }
(four) out of team
template <class T> T seqQueue<T>::deQueue() { //Throw an exception if the queue is empty if (empty()) throw outOfRange(); //Move tail pointer front = (front + 1) % maxSize; //x team entry return data[front]; }
(V) team leader
template <class T> T seqQueue<T>::getHead() const { if (empty()) throw outOfRange(); //Returns the team head element without moving the team head pointer return data[(front + 1) % maxSize]; }
(VI) expand the queue space
template <class T> void seqQueue<T>::resize() { T *p = data; data = new T[2 *maxSize]; for(int i = 1; i < size(); ++i) //Duplicate elements data[i] = p[(front + i) % maxSize]; //Set team head and tail pointer front = 0; rear = size(); maxSize *= 2; delete p; }
Chain queue
Using chain storage structure to represent queue is called chain queue. Using single chain table without head node to represent queue. The header is the queue head and the tail is the queue tail. Two pointers are needed to point to the queue head element and the queue tail element respectively. One of the advantages of this storage structure is that the queue will not be full.

(I) type definition of sequence queue
#ifndef _LINKQUEUE_H_ #define _LINKQUEUE_H_ #include <iostream> #include "Queue.h" template <class T> class linkQueue:public Queue<T> { private: struct node { T data; node *next; node (const T &x, node *N = NULL) { data = x; next = N; } node ():next(NULL){} ~node () {} }; node *front, *rear; public: linkQueue(){front = rear = NULL;}; ~linkQueue() {clear();} //Clear queue void clear(); //Sentence blank bool empty() const {return front == NULL;} //queue length int size() const; //Join the team void enQueue(const T &x); //Team out T deQueue(); //Team leader element T getHead() const; }; #endif
(II) clear the queue
template <class T> void linkQueue<T>::clear() { node *p; //Release all nodes in the queue while(front != NULL) { p = front; front = front -> next; delete p; } //Modify tail pointer rear = NULL; }
(III) find the queue length
template <class T> int linkQueue<T>::size() const { node *p = front; int count = 0; while(p) { count++; p = p -> next; } return count; }
(four) join the team
template <class T> void linkQueue<T>::enQueue(const T &x) { if(rear == NULL) front = rear = new node(x); else { rear -> next = new node(x); rear = rear -> next; } }
(five) out of team
template <class T> T linkQueue<T>::deQueue() { //Throw an exception if the queue is empty if (empty()) throw outOfRange(); node *p = front; //Save team leader element T value = front -> data; front = front -> next; if (front == NULL) rear = NULL; delete p; return value; }
(VI) team leader
template <class T> T linkQueue<T>::getHead() const { if (empty()) throw outOfRange(); return front -> data; }
Ending:
If there are any shortcomings or mistakes in the article, please leave a message and share your ideas. Thank you for your support!
If you can help, then pay attention to me! If you prefer the way of reading WeChat articles, you can pay attention to my public number.
We don't know each other here, but we are working hard for our dreams.
A public figure that persists in pushing original development technology articles: ideal two days
