Tip: After the article is written, the catalog can be generated automatically, how to generate the help document to the right

Preface

This experiment uses KNN algorithm to recognize handwritten digits. For simplicity, only the digits 0 to 9 need to be recognized have been processed into the same color and size using graphics processing software: black and white image with 32 pixels wide and 32 pixels high, and converted into text format.

Tip: The following is the main body of this article. The following cases can be used as reference.

1. EXPERIMENTAL STEPS

(1) Collect data: provide text files;

(2) Preparing data: Write the function classify0() to convert the image format to the List format used by the classifier;

(3) Test algorithm: Write function to use some of the provided datasets as test samples, test samples and areas of non-test samples

The difference is that the test sample is data that has been classified, and if the predicted classification is different from the actual category, it is marked as one

Error.

2. Process of Use

1. Collect data: provide text files

The dataset consists of two parts, one is a training dataset with a total of 1934 data, the other is a test dataset with a total of 946 data. All the naming formats in the two datasets are uniform, such as "3_12.txt", which represents the twelfth sample of number 5, in order to extract the true label of the sample.

 

2. Preparing data: converting images to test vectors

Format the image as a vector to convert each 32x32 binary image matrix to a vector of 1x1024. Write the function img2vector to convert the image to a vector: the function creates a Numpy array of 1X1024, opens the given file, reads out the first 32 lines of the file, stores the first 32 character values of each line in the Numpy array, and returns the data.

The code is as follows:

#Preparing data: Converting images to data vectors
def img2vector(filename):
    '''
    Convert Image to Vector
    :param filename: File directory name
    :return: Vector Array
    '''
    #Create Vector
    returnVect = zeros((1,1024))
    #Open the data file and read each line
    fr = open(filename)
    for i in range(32):
        #Loop through each line
        lineStr = fr.readline()
        for j in range(32):
            #Converts the first 32 characters of each line to int and stores them in a vector
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

Testing the img2vector function:

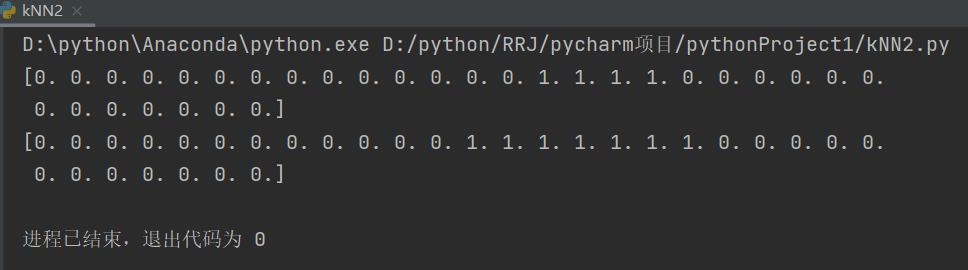
testVector = img2vector("digits/testDigits/0_13.txt")
    print(testVector[0,0:31])
    print(testVector[0, 32:63])

3. Test algorithm: Recognize handwritten numbers using k-nearest neighbor algorithm

Write the handwritingClassTest() function.

The code is as follows:

#Handwritten Digital Recognition System Test Code
def handwritingClassTest():
    #List of class labels for sample data
    hwLabels = []
    #List of sample data files
    trainingFileList = os.listdir("digits/trainingDigits")
    #Get Lines of File
    m = len(trainingFileList)
    #Initialize Sample Data Matrix
    trainingMat = zeros((m,1024))
    #Read all sample data sequentially to the data matrix
    for i in range(m):
        #Extracting numbers from file names
        fileNameStr = trainingFileList[i]
        #Remove.txt
        fileStr = fileNameStr.split('.')[0]
        #Gets the first character, which number it is
        classNumStr = int(fileStr.split('_')[0])
        #Save label
        hwLabels.append(classNumStr)
        #Sample data into a matrix
        trainingMat[i,:] = img2vector('digits/trainingDigits/%s' %(fileNameStr))
    #Read test data
    testFileList = os.listdir('digits/testDigits')
    #Initialization error rate
    errorCount = 0.0
    mTest = len(testFileList)
    errfile = []
    #Loop through each test data file
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]
        classNumStr = int(fileStr.split('_')[0])
        #Extracting data vectors
        vectorUnderTest = img2vector('digits/testDigits/%s' %(fileNameStr))
        #Classify data files
        classifierResult = classify0(vectorUnderTest,trainingMat,hwLabels ,3)    #Pass-by k=3
        #Output k-Nearest Neighbor algorithm classification results and true classification
        print('the classifier came back with: %d,the real answer is: %d' %(classifierResult,classNumStr))
        #Determining whether the k-nearest neighbor algorithm is accurate
        if(classifierResult != classNumStr):
            errorCount +=1.0
            errfile.append(fileNameStr)
    print('\n the total number of errors is: %d' %(errorCount))          #Total number of errors
    print('Wrong is:%s ;' %[i for i in errfile])
    print('\n the total error rate is: %f' %(errorCount/float(mTest)))   #Total error rate

Store the contents of the files in the trainingDigits directory in a list, and you can get how many files are in the directory and store them in the variable m. Next, create a training matrix with 1024 columns in m rows, where each row of data stores an image. We can parse the classification number from the file name. For example, 9_45.txt has a classification of 9, which is a number 9.The 45th instance. Then we can store the class code in the hwLabels vector and use the img2vector function to load the image. Then we do a similar operation on the files in the testDigits directory, except that instead of loading the files in this directory into the matrix, we use the classify0() function to test each file in that directory.

Test the handwritingClassTest() function:

    #start time
    start = time.perf_counter()
    #Test the output of handwritingClassTest()
    handwritingClassTest()
    end = time.perf_counter()
    print("Running time:%ds" %(end-start))

Test results:

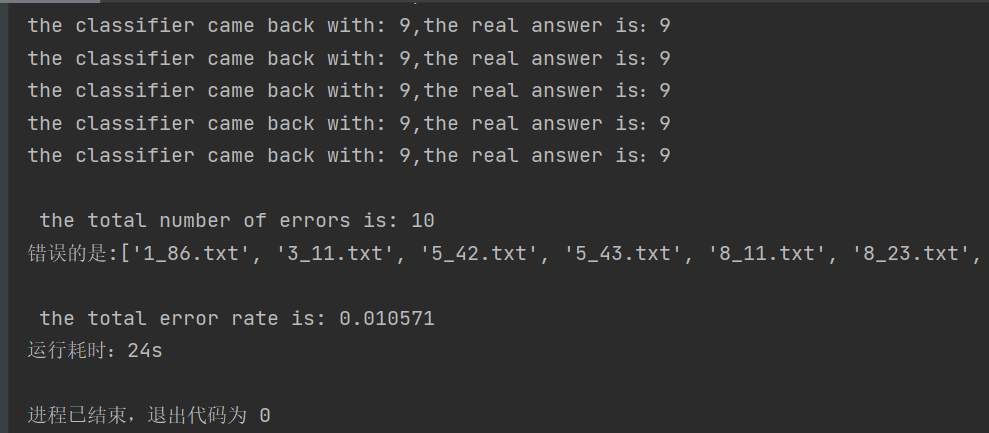
When K=3, the accuracy rate of 946 numbers tested was 98.94%, only 10 numbers predicted incorrectly and the accuracy rate was high, but the running efficiency was low, reaching 24 seconds. Because each test data had to be calculated from 1934 training data, and each calculation contained 1024 dimension floating point operations, the main reason for the inefficiency of this experiment was the high number of multidimensional calculations..

Change K=3 to K=5 to verify accuracy:

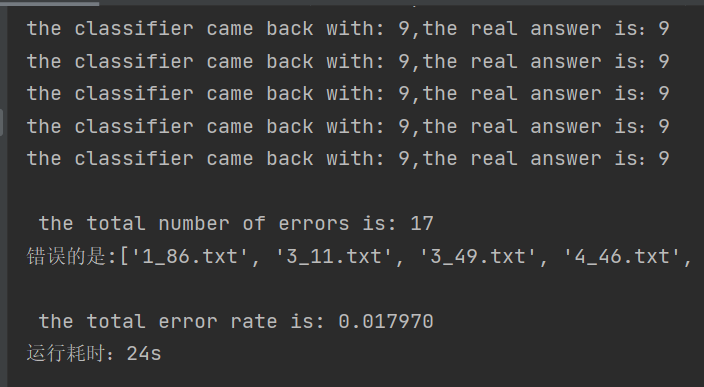
The error rate rises to 1.8% when K becomes 5, so a relative K=3 is appropriate.

Selecting a smaller K value is equivalent to predicting with training instances in a smaller field, and the approximation error is reduced. Only training instances that are close to or similar to the input instances will play a role in predicting the results. A smaller K value means that the overall model becomes complex and easy to fit. Selecting a larger K value is equivalent to predicting with training instances in a larger field.At this time, training instances that are far from (not similar to) the input instances will also work on the predictor, making the prediction error, and the increase of K value means that the overall model becomes simple and easy to underfit.

In practice, the K value usually takes a smaller value, such as choosing the optimal K value by using cross-validation (simply, dividing the training data into two groups: training set and validation set).

Ten data were extracted from the test sample set and validated:

The results are as follows:

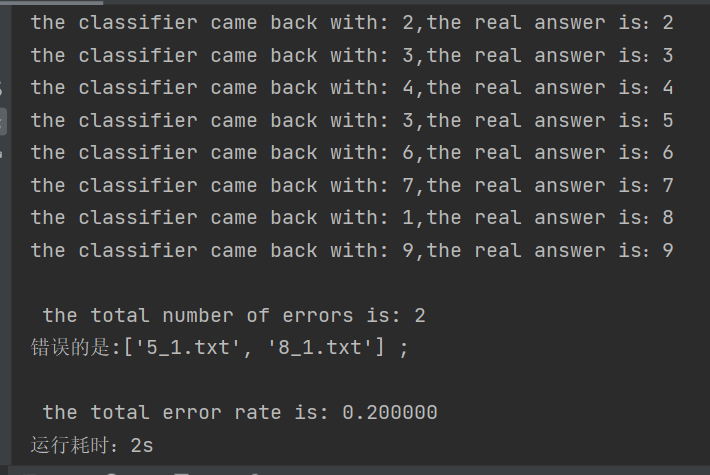
Two out of 10 test results are wrong. The text file for observing prediction errors is as follows:

5_1.txt predicts 3 and the actual result is 5.

The preparation of data is therefore considered important, as is the accuracy of functions that convert image data to text data for handwritten number recognition using the K-Nearest Neighbor algorithm.

The url network requested data used here.

summary

K-Nearest neighbor algorithm:

Advantages: 1. Simple and effective classification algorithm, a lazy-learningsuanfa;

2. No training required, the training time complexity is 0;

3. Insensitive to outliers (individual noise data has little effect on the results).

Disadvantages: 1. High computational complexity, high spatial complexity, KNN algorithm computational complexity is proportional to the number of documents in the training set, if

If the total number is N, the classification time complexity is O(N).

2. Memory consumption: All datasets must be saved;

3. Time-consuming and inefficient operation;

4. No intrinsic meaning of any data can be given.