After installing Tensorflow, install keras to use TF as the back-end by default. The code of keras to realize convolution network is very simple, and the callback class in keras provides a method to detect variables in the model training process, which can adjust the learning efficiency and some parameters of the model in time according to the situation of detecting variables. In the following example, MNIST data is used as the test
import pandas as pd import numpy as np import matplotlib.pyplot as plt import matplotlib.image as pimg import seaborn as sb # A painting module based on matplotlib, supporting numpy,pandas and other data structures %matplotlib inline from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix # Confusion matrix import itertools # keras from keras.utils import to_categorical #Digital tag transformed into one-hot code from keras.models import Sequential from keras.layers import Dense,Dropout,Flatten,Conv2D,MaxPool2D from keras.optimizers import RMSprop from keras.preprocessing.image import ImageDataGenerator from keras.callbacks import ReduceLROnPlateau
Using TensorFlow backend.
# Set painting style sb.set(style='white', context='notebook', palette='deep')
# Loading data
train_data = pd.read_csv('data/train.csv')
test_data = pd.read_csv('data/test.csv')
#train_x = train_data.drop(labels=['label'],axis=1) # Remove label column
train_x = train_data.iloc[:,1:]
train_y = train_data.iloc[:,0]
del train_data # Free up some memory
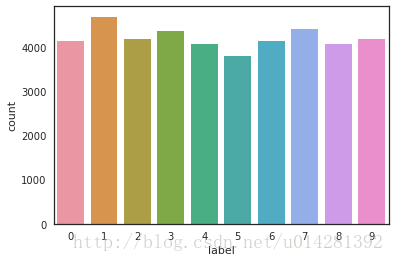
# Observe the distribution of training data g = sb.countplot(train_y) train_y.value_counts()
1 4684 7 4401 3 4351 9 4188 2 4177 6 4137 0 4132 4 4072 8 4063 5 3795 Name: label, dtype: int64
train_x.isnull().describe() # Check for a true value
train_x.isnull().any().describe()
count 784 unique 1 top False freq 784 dtype: object
test_data.isnull().any().describe()
count 784 unique 1 top False freq 784 dtype: object
# normalization train_x = train_x/255.0 test_x = test_data/255.0
del test_data
Transform the shape of data
# reshape trian_x, test_x #train_x = train_x.values.reshape(-1, 28, 28, 1) #test_x = test_x.values.reshape(-1, 28, 28, 1) train_x = train_x.as_matrix().reshape(-1, 28, 28, 1) test_x = test_x.as_matrix().reshape(-1, 28, 28, 1)
# Convert the label column to one hot encoding format train_y = to_categorical(train_y, num_classes = 10)
Separate validation data from data
#One tenth of training data is used as verification data random_seed = 3 train_x , val_x , train_y, val_y = train_test_split(train_x, train_y, test_size=0.1, random_state=random_seed)
A training sample
plt.imshow(train_x[0][:,:,0])
Building CNN with Keras
model = Sequential() # First convolution layer, 32 convolution kernels, size 5x5, convolution mode save, activation function relu, input tensor size model.add(Conv2D(filters= 32, kernel_size=(5,5), padding='Same', activation='relu',input_shape=(28,28,1))) model.add(Conv2D(filters= 32, kernel_size=(5,5), padding='Same', activation='relu')) # Pool layer, pool core size 2x2 model.add(MaxPool2D(pool_size=(2,2))) # Randomly discard one quarter of network connections to prevent over fitting model.add(Dropout(0.25)) model.add(Conv2D(filters= 64, kernel_size=(3,3), padding='Same', activation='relu')) model.add(Conv2D(filters= 64, kernel_size=(3,3), padding='Same', activation='relu')) model.add(MaxPool2D(pool_size=(2,2), strides=(2,2))) model.add(Dropout(0.25)) # Full connection layer, expand operation, model.add(Flatten()) # Add the number of hidden layer neurons and activation function model.add(Dense(256, activation='relu')) model.add(Dropout(0.25)) # Output layer model.add(Dense(10, activation='softmax'))
# Set optimizer # lr: learning efficiency, decay: attenuation value of lr optimizer = RMSprop(lr = 0.001, decay=0.0)
# Compilation model # Loss: loss function, metrics: corresponding performance evaluation function model.compile(optimizer=optimizer, loss = 'categorical_crossentropy',metrics=['accuracy'])
Create an instance of the callback class
# The callback class of keras provides the ability to track target values and dynamically adjust learning efficiency
# Monitor: the quantity to be monitored, here is the verification accuracy rate
# Animation: after three rounds of iterations, the target amount of monitoring is still unchanged, and the learning efficiency will be adjusted
# verbose: information display mode, to 0 or 1
# Factor: each time the learning rate is reduced, the learning rate will be reduced in the form of lr = lr*factor
# Mode: "auto", "min", "max". In min mode, if the detection value triggers the decrease of learning rate. In max mode, when the detection value no longer increases, the learning rate decreases.
# epsilon: threshold value used to determine whether to enter the "plain area" of the detection value
# Cooldown: after the learning rate is reduced, normal operation will be resumed after cooldown epoch s
# Min? LR: the lower limit of learning rate
learning_rate_reduction = ReduceLROnPlateau(monitor = 'val_acc', patience = 3,
verbose = 1, factor=0.5, min_lr = 0.00001)
epochs = 40 batch_size = 100
Data enhancement processing
# Data enhancement processing can improve the generalization ability of the model, and also can effectively avoid the over fitting of the model
# Rotation? Range: angle of rotation
# Zoom range: randomly scale an image
# Width? Shift? Range: ratio of horizontal movement to image width
# height_shift_range
# Horizontal inverted
# Vertical? FILP: reverse in the vertical direction
data_augment = ImageDataGenerator(rotation_range= 10,zoom_range= 0.1,
width_shift_range = 0.1,height_shift_range = 0.1,
horizontal_flip = False, vertical_flip = False)
Training model
history = model.fit_generator(data_augment.flow(train_x, train_y, batch_size=batch_size),
epochs= epochs, validation_data = (val_x,val_y),
verbose =2, steps_per_epoch=train_x.shape[0]//batch_size,
callbacks=[learning_rate_reduction])
Epoch 1/40 359s - loss: 0.4529 - acc: 0.8498 - val_loss: 0.0658 - val_acc: 0.9793 Epoch 2/40 375s - loss: 0.1188 - acc: 0.9637 - val_loss: 0.0456 - val_acc: 0.9848 Epoch 3/40 374s - loss: 0.0880 - acc: 0.9734 - val_loss: 0.0502 - val_acc: 0.9845 Epoch 4/40 375s - loss: 0.0750 - acc: 0.9767 - val_loss: 0.0318 - val_acc: 0.9902 Epoch 5/40 374s - loss: 0.0680 - acc: 0.9800 - val_loss: 0.0379 - val_acc: 0.9888 Epoch 6/40 369s - loss: 0.0584 - acc: 0.9823 - val_loss: 0.0267 - val_acc: 0.9910 Epoch 7/40 381s - loss: 0.0556 - acc: 0.9832 - val_loss: 0.0505 - val_acc: 0.9824 Epoch 8/40 381s - loss: 0.0531 - acc: 0.9842 - val_loss: 0.0236 - val_acc: 0.9912 Epoch 9/40 376s - loss: 0.0534 - acc: 0.9839 - val_loss: 0.0310 - val_acc: 0.9910 Epoch 10/40 379s - loss: 0.0537 - acc: 0.9848 - val_loss: 0.0274 - val_acc: 0.9917 Epoch 11/40 375s - loss: 0.0501 - acc: 0.9856 - val_loss: 0.0254 - val_acc: 0.9931 Epoch 12/40 382s - loss: 0.0492 - acc: 0.9860 - val_loss: 0.0212 - val_acc: 0.9924 Epoch 13/40 380s - loss: 0.0482 - acc: 0.9864 - val_loss: 0.0259 - val_acc: 0.9919 Epoch 14/40 373s - loss: 0.0488 - acc: 0.9858 - val_loss: 0.0305 - val_acc: 0.9905 Epoch 15/40 Epoch 00014: reducing learning rate to 0.000500000023749. 370s - loss: 0.0493 - acc: 0.9853 - val_loss: 0.0259 - val_acc: 0.9919 Epoch 16/40 367s - loss: 0.0382 - acc: 0.9888 - val_loss: 0.0176 - val_acc: 0.9936 Epoch 17/40 376s - loss: 0.0376 - acc: 0.9891 - val_loss: 0.0187 - val_acc: 0.9945 Epoch 18/40 376s - loss: 0.0410 - acc: 0.9885 - val_loss: 0.0220 - val_acc: 0.9926 Epoch 19/40 371s - loss: 0.0385 - acc: 0.9886 - val_loss: 0.0194 - val_acc: 0.9933 Epoch 20/40 372s - loss: 0.0345 - acc: 0.9894 - val_loss: 0.0186 - val_acc: 0.9938 Epoch 21/40 Epoch 00020: reducing learning rate to 0.000250000011874. 375s - loss: 0.0395 - acc: 0.9888 - val_loss: 0.0233 - val_acc: 0.9945 Epoch 22/40 369s - loss: 0.0313 - acc: 0.9907 - val_loss: 0.0141 - val_acc: 0.9955 Epoch 23/40 376s - loss: 0.0308 - acc: 0.9910 - val_loss: 0.0187 - val_acc: 0.9945 Epoch 24/40 374s - loss: 0.0331 - acc: 0.9908 - val_loss: 0.0170 - val_acc: 0.9940 Epoch 25/40 372s - loss: 0.0325 - acc: 0.9904 - val_loss: 0.0166 - val_acc: 0.9948 Epoch 26/40 Epoch 00025: reducing learning rate to 0.000125000005937. 373s - loss: 0.0319 - acc: 0.9904 - val_loss: 0.0167 - val_acc: 0.9943 Epoch 27/40 372s - loss: 0.0285 - acc: 0.9915 - val_loss: 0.0138 - val_acc: 0.9950 Epoch 28/40 375s - loss: 0.0280 - acc: 0.9913 - val_loss: 0.0150 - val_acc: 0.9950 Epoch 29/40 Epoch 00028: reducing learning rate to 6.25000029686e-05. 377s - loss: 0.0281 - acc: 0.9924 - val_loss: 0.0158 - val_acc: 0.9948 Epoch 30/40 374s - loss: 0.0265 - acc: 0.9920 - val_loss: 0.0134 - val_acc: 0.9952 Epoch 31/40 378s - loss: 0.0270 - acc: 0.9922 - val_loss: 0.0128 - val_acc: 0.9957 Epoch 32/40 372s - loss: 0.0237 - acc: 0.9930 - val_loss: 0.0133 - val_acc: 0.9957 Epoch 33/40 375s - loss: 0.0237 - acc: 0.9931 - val_loss: 0.0138 - val_acc: 0.9955 Epoch 34/40 371s - loss: 0.0276 - acc: 0.9920 - val_loss: 0.0135 - val_acc: 0.9962 Epoch 35/40 373s - loss: 0.0259 - acc: 0.9920 - val_loss: 0.0136 - val_acc: 0.9952 Epoch 36/40 369s - loss: 0.0249 - acc: 0.9924 - val_loss: 0.0126 - val_acc: 0.9952 Epoch 37/40 370s - loss: 0.0257 - acc: 0.9923 - val_loss: 0.0130 - val_acc: 0.9960 Epoch 38/40 Epoch 00037: reducing learning rate to 3.12500014843e-05. 374s - loss: 0.0252 - acc: 0.9926 - val_loss: 0.0136 - val_acc: 0.9950 Epoch 39/40 372s - loss: 0.0246 - acc: 0.9927 - val_loss: 0.0134 - val_acc: 0.9957 Epoch 40/40 371s - loss: 0.0247 - acc: 0.9929 - val_loss: 0.0139 - val_acc: 0.9950
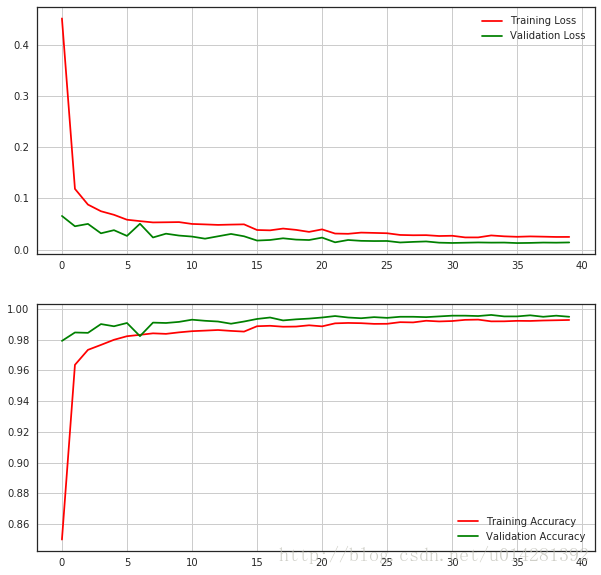
In the process of training, there are several conditions that trigger the learning efficiency decay. When val'acc does not increase for three consecutive rounds, it will adjust the learning efficiency to the current half. After the adjustment, val'acc has a significant increase, but in the last few rounds, the model may have converged
# learning curves fig,ax = plt.subplots(2,1,figsize=(10,10)) ax[0].plot(history.history['loss'], color='r', label='Training Loss') ax[0].plot(history.history['val_loss'], color='g', label='Validation Loss') ax[0].legend(loc='best',shadow=True) ax[0].grid(True) ax[1].plot(history.history['acc'], color='r', label='Training Accuracy') ax[1].plot(history.history['val_acc'], color='g', label='Validation Accuracy') ax[1].legend(loc='best',shadow=True) ax[1].grid(True)
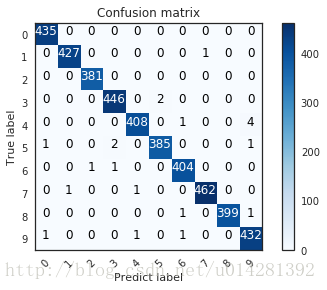
# Confusion matrix
def plot_sonfusion_matrix(cm, classes, normalize=False, title='Confusion matrix',cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float')/cm.sum(axis=1)[:,np.newaxis]
thresh = cm.max()/2.0
for i,j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j,i,cm[i,j], horizontalalignment='center',color='white' if cm[i,j] > thresh else 'black')
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predict label')
Confusing proof of validation data
pred_y = model.predict(val_x) pred_label = np.argmax(pred_y, axis=1) true_label = np.argmax(val_y, axis=1) confusion_mat = confusion_matrix(true_label, pred_label) plot_sonfusion_matrix(confusion_mat, classes = range(10))