Preface:
Learning is like cabbage, one layer by one gradually approaching the cabbage, but you can never dial the innermost layer, infinitely close, before I wrote an algorithm about KNN, using Python, I feel that recently there is a new understanding, understanding and a little deeper.
Introduce the algorithm
know
Programming is often said to learn three sentence structures, walk around the world without fear, think about the operation of people are basically three steps, recognition (perception), judgment (decision), operation (action), such as you write a word, first to identify the paper and pen, and then decide where to write, and then open. Start writing, but the three are nested. When you recognize paper and pen, you do these three steps. 1 recognizes and sees 2 to determine whether paper 3 is taken over and put on the table or not.
Then we often have the question of what this thing is, is this a pen? I'll just take it, or I'm not looking for it, so what's the identification of this thing? In fact, it is a problem of classification. If this is a pen, then I have used a pen before and know that it can write. If it is a pencil, it needs a pencil sharpener or knife to write for a period of time. If it is an automatic pen, it needs a pencil core for a period of time, and it is easy to break down if it is a pen. If it is an oil pen, we can change the pen core after classification. With the help of previous experience of this type of items, new judgment operations are carried out.
KNN algorithm is an algorithm for solving classification problems, and it is a kind of machine learning algorithm. k-Nearest Neighbor means the nearest neighbor to K.
How to Classify
1 Simple Understanding
As shown in the figure, this picture is classic. It has blue squares and red triangles, which represent two types of data. Now put an unknown type of data into a green circle. Is it a triangle or a square? If k=3, that is to find the nearest three data from the green. If there are more triangles, we can judge that it is a triangle class. If there are more squares, we can judge that it is a triangle class. If there are three squares and two triangles in Figure k=5, the K value has a great influence on classification.
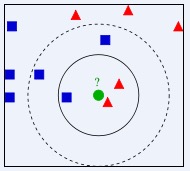
After a brief understanding, you will surely have doubts, do I put the green circles in one place to categorize them? Of course not. Let's continue with the following examples.
Category 2 Films
|
Film Name |
Fighting lens |
Kissing lens |
Film Types |
|
Film 1 |
10 |
101 |
Affectional film |
|
Movie 2 |
7 |
89 |
Affectional film |
|
Film 3 |
108 |
5 |
Action movie |
|
Film 4 |
115 |
8 |
Action movie |
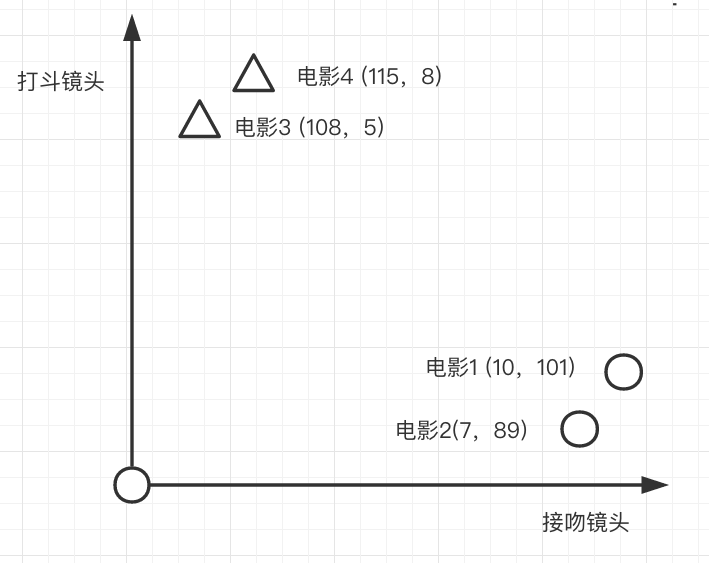
If there is now a movie 5 fighting lens 12 kissing lens 120, according to the knn algorithm if k=3 what kind of movie is it?
It's love movies, because the three closest movies to Movie 5 are Movie 4, Movie 3 and Movie 1, two of which are love movies, so we classify this unknown movie into love movies.
How to judge distance?
In the plane rectangular coordinate system, the distance calculation is

4 Why is the nearer the distance one kind?
Each point is an entity, each entity has multiple attributes, multiple attributes, according to multiple attributes to calculate the distance between two points, if closer, it shows that the two points are approximately similar, there are many formulas for calculating distance, the Euclidean distance will be used below.
Algorithmic Principle
In fact, the principle of KNN algorithm is very simple, that is, to find K neighbors, what type is the most near, to determine the current entity is what type, generally K is odd, if it is even, 2 A type and 2 B type, it can not be judged, right.
The problem is, if we draw a picture, we can easily distinguish the nearest K with our eyes, but in fact, there are more than two dimensions of data, such as movies and comedies, and laughing pictures to judge whether it is a comedy or not. At that time, it was three-dimensional and could not be painted on a plane. Entities have many dimensions, and there are special distance formulas for calculating distance in multi-dimensions.
Think about Realization
Consideration 1
1 Put all entities in an array
2 traverse the array to calculate the distance of each element to be added
3 Sort by distance
4. Take out the nearest K elements
Idea: Although this can be achieved, it's too expensive for every element to cycle once to calculate distance.
Thinking 2
In fact, I don't think much about reading books, which are implemented by kd tree.
1. Building kd tree
2. Use kd tree to find the nearest K
How to construct kd tree
First of all, the kd tree is a tree, which is a binary tree. Well, 0, because data generally has multiple dimensions. Here, take two dimensions for example. If you want to see two dimensions, you need to look at one dimension first. 1. 23. 4567 to build a tree.
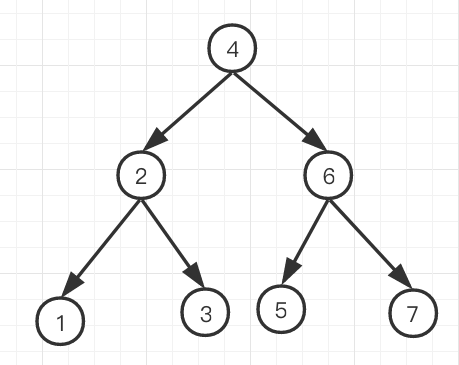
The first step is to find the median.
The second part is divided by median. The smaller part is on the left and the larger part is on the right.
The third step is to re-execute the first step according to the division into two groups 123 and 567, respectively, until indivisible
Is one dimension simple? Look at two dimensions.
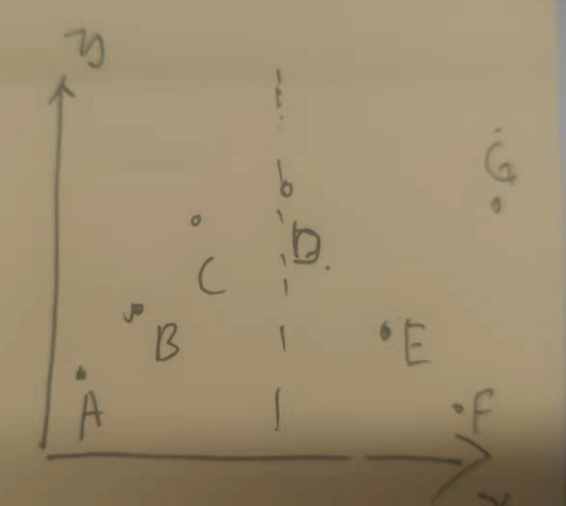
Data sets {A(1,3),B(12.4),C(3,9),D(31,22),E(,34,11),F(,100,3),G(123,22)}
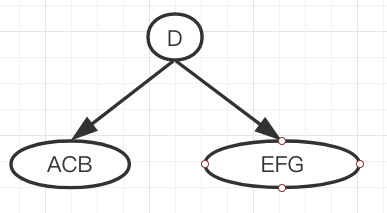
The first step is to find the median by x
List x A (1), B (12), C (3), D (31), E (34), F (100), G (123)
Sort x A (1), C (3), B (12), D (31), E (34), F (100), G (123)
Median division A(1),C(3),B(12), D(31), E (34), F (100), G (123)
Now the tree is like this.
The second step is to divide by y
List y sort
A(3),B(4),C(9)
F(3),E(11),G(22)
After partitioning, trees become like this.
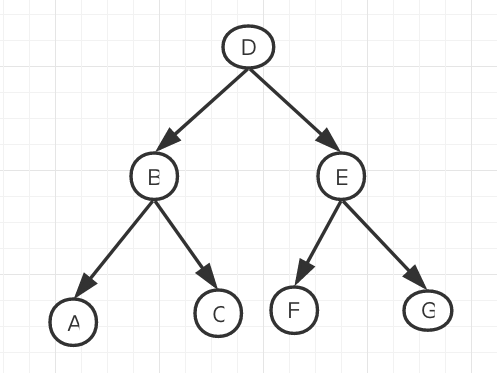
Step 3
If you haven't finished building, repeat the first and second steps, how many dimensions are there, and divide each layer of tree into circular dimensions.
How to build version of kd tree graph

java code
package KD tree;
public class Node implements Comparable<KD tree.Node> {
public double[] data;//The data of nodes on a tree is a multidimensional vector
public double distance;//The distance from the current query point is not initialized
public KD tree.Node left, right, parent;//Left and right child nodes and parent nodes
public int dim = -1;//Dimension of judgment when building a tree
public Node(double[] data) {
this.data = data;
}
/**
* Returns the value on the specified index
*
* @param index
* @return
*/
public double getData(int index) {
if (data == null || data.length <= index)
return Integer.MIN_VALUE;
return data[index];
}
@Override
public int compareTo(KD tree.Node o) {
if (this.distance > o.distance)
return 1;
else if (this.distance == o.distance)
return 0;
else return -1;
}
/**
* Calculate the distance back to Euclidean distance here
*
* @param that
* @return
*/
public double computeDistance(KD tree.Node that) {
if (this.data == null || that.data == null || this.data.length != that.data.length)
return Double.MAX_VALUE;//The farthest distance is when something goes wrong.
double d = 0;
for (int i = 0; i < this.data.length; i++) {
d += Math.pow(this.data[i] - that.data[i], 2);
}
return Math.sqrt(d);
}
public String toString() {
if (data == null || data.length == 0)
return null;
StringBuilder sb = new StringBuilder();
for (int i = 0; i < data.length; i++)
sb.append(data[i] + " ");
sb.append(" d:" + this.distance);
return sb.toString();
}
}
package KD tree;
public class BinaryTreeOrder {
public void preOrder(Node root) {
if (root != null) {
System.out.print(root.toString());
preOrder(root.left);
preOrder(root.right);
}
}
}
package KD tree;
import java.util.ArrayList;
import java.util.List;
public class kd_main {
public static void main(String[] args) {
List<Node> nodeList = new ArrayList<Node>();
nodeList.add(new Node(new double[]{5, 4}));
nodeList.add(new Node(new double[]{9, 6}));
nodeList.add(new Node(new double[]{8, 1}));
nodeList.add(new Node(new double[]{7, 2}));
nodeList.add(new Node(new double[]{2, 3}));
nodeList.add(new Node(new double[]{4, 7}));
nodeList.add(new Node(new double[]{4, 3}));
nodeList.add(new Node(new double[]{1, 3}));
kd_main kdTree = new kd_main();
//Constructing Binary Tree
Node root = kdTree.buildKDTree(nodeList, 0);
//Printing
new BinaryTreeOrder().preOrder(root);
for (Node node : nodeList) {
String left = "empty";
String right = "empty";
if (node.left != null) {
left = node.left.toString();
}
if (node.right != null) {
right = node.right.toString();
}
System.out.println(node.toString() + "-->" + left + "-->" + right);
}
System.out.println(root);
System.out.println(kdTree.searchKNN(root, new Node(new double[]{2.1, 3.1}), 2));
System.out.println(kdTree.searchKNN(root, new Node(new double[]{2, 4.5}), 1));
System.out.println(kdTree.searchKNN(root, new Node(new double[]{2, 4.5}), 3));
System.out.println(kdTree.searchKNN(root, new Node(new double[]{6, 1}), 5));
}
/**
* Constructing kd tree to return to root node
*
* @param nodeList
* @param index
* @return
*/
public Node buildKDTree(List<Node> nodeList, int index) {
if (nodeList == null || nodeList.size() == 0)
return null;
quickSortForMedian(nodeList, index, 0, nodeList.size() - 1);//Median ranking
Node root = nodeList.get(nodeList.size() / 2);//Median as root node
root.dim = index;
List<Node> leftNodeList = new ArrayList<Node>();//Nodes placed in the left area include nodes with median equivalents--
List<Node> rightNodeList = new ArrayList<Node>();
for (Node node : nodeList) {
if (root != node) {
if (node.getData(index) <= root.getData(index))
leftNodeList.add(node);//The left subregion contains nodes equal to the median
else
rightNodeList.add(node);
}
}
//From which dimension is the calculation segmented?
int newIndex = index + 1;//Enter the next dimension
if (newIndex >= root.data.length)
newIndex = 0;//Calculate from dimension 0
root.left = buildKDTree(leftNodeList, newIndex);//Add left and right subregions
root.right = buildKDTree(rightNodeList, newIndex);
if (root.left != null)
root.left.parent = root;//Add parent pointer
if (root.right != null)
root.right.parent = root;//Add parent pointer
return root;
}
/**
* Query the nearest neighbor
*
* @param root kd tree
* @param q Query Points
* @param k
* @return
*/
public List<Node> searchKNN(Node root, Node q, int k) {
List<Node> knnList = new ArrayList<Node>();
searchBrother(knnList, root, q, k);
return knnList;
}
/**
* searhchBrother
*
* @param knnList
* @param k
* @param q
*/
public void searchBrother(List<Node> knnList, Node root, Node q, int k) {
// Node almostNNode=root; // approximate nearest point
Node leafNNode = searchLeaf(root, q);
double curD = q.computeDistance(leafNNode);//The distance between the nearest approximation point and the query point is the radius of the sphere.
leafNNode.distance = curD;
maintainMaxHeap(knnList, leafNNode, k);
System.out.println("leaf1" + leafNNode.getData(leafNNode.parent.dim));
while (leafNNode != root) {
if (getBrother(leafNNode) != null) {
Node brother = getBrother(leafNNode);
System.out.println("brother1" + brother.getData(brother.parent.dim));
if (curD > Math.abs(q.getData(leafNNode.parent.dim) - leafNNode.parent.getData(leafNNode.parent.dim)) || knnList.size() < k) {
//It is possible to have more approximate points in another subregion.
searchBrother(knnList, brother, q, k);
}
}
System.out.println("leaf2" + leafNNode.getData(leafNNode.parent.dim));
leafNNode = leafNNode.parent;//Return to the previous level
double rootD = q.computeDistance(leafNNode);//The distance between the nearest approximation point and the query point is the radius of the sphere.
leafNNode.distance = rootD;
maintainMaxHeap(knnList, leafNNode, k);
}
}
/**
* Get sibling nodes
*
* @param node
* @return
*/
public Node getBrother(Node node) {
if (node == node.parent.left)
return node.parent.right;
else
return node.parent.left;
}
/**
* Query to leaf nodes
*
* @param root
* @param q
* @return
*/
public Node searchLeaf(Node root, Node q) {
Node leaf = root, next = null;
int index = 0;
while (leaf.left != null || leaf.right != null) {
if (q.getData(index) < leaf.getData(index)) {
next = leaf.left;//Enter the left side
} else if (q.getData(index) > leaf.getData(index)) {
next = leaf.right;
} else {
//Determine which sub-region is nearer to the left and right when the mid-range is taken
if (q.computeDistance(leaf.left) < q.computeDistance(leaf.right))
next = leaf.left;
else
next = leaf.right;
}
if (next == null)
break;//The next node is the end of space-time.
else {
leaf = next;
if (++index >= root.data.length)
index = 0;
}
}
return leaf;
}
/**
* Maintain a maximum k heap
*
* @param listNode
* @param newNode
* @param k
*/
public void maintainMaxHeap(List<Node> listNode, Node newNode, int k) {
if (listNode.size() < k) {
maxHeapFixUp(listNode, newNode);//Insufficient k heaps are repaired directly up
} else if (newNode.distance < listNode.get(0).distance) {
//It is smaller than the top of the heap and needs to be repaired downward to cover the top of the heap.
maxHeapFixDown(listNode, newNode);
}
}
/**
* Top-down repair will cover the first node
*
* @param listNode
* @param newNode
*/
private void maxHeapFixDown(List<Node> listNode, Node newNode) {
listNode.set(0, newNode);
int i = 0;
int j = i * 2 + 1;
while (j < listNode.size()) {
if (j + 1 < listNode.size() && listNode.get(j).distance < listNode.get(j + 1).distance)
j++;//The first condition is that the right subtree is not empty.
if (listNode.get(i).distance >= listNode.get(j).distance)
break;
Node t = listNode.get(i);
listNode.set(i, listNode.get(j));
listNode.set(j, t);
i = j;
j = i * 2 + 1;
}
}
private void maxHeapFixUp(List<Node> listNode, Node newNode) {
listNode.add(newNode);
int j = listNode.size() - 1;
int i = (j + 1) / 2 - 1;//i is the parent node of j
while (i >= 0) {
if (listNode.get(i).distance >= listNode.get(j).distance)
break;
Node t = listNode.get(i);
listNode.set(i, listNode.get(j));
listNode.set(j, t);
j = i;
i = (j + 1) / 2 - 1;
}
}
/**
* The array size/2 returned after searching for a median using fast-padding is the median
*
* @param nodeList
* @param index A certain dimension
* @param left
* @param right
*/
private void quickSortForMedian(List<Node> nodeList, int index, int left, int right) {
if (left >= right || nodeList.size() <= 0)
return;
Node kn = nodeList.get(left);//Take out a node at random
double k = kn.getData(index);//Gets the value of the vector specified index
int i = left, j = right;
//Controlling the end conditions of each traversal, i and j meet, in short, to put the left side smaller than kn and the right side larger than kn.
while (i < j) {
//Find a value less than i from right to left and fill in the position of i
while (nodeList.get(j).getData(index) >= k && i < j)
j--;
nodeList.set(i, nodeList.get(j));
//Find a value greater than the value at i from left to right and fill in the position of j
while (nodeList.get(i).getData(index) <= k && i < j)
i++;
nodeList.set(j, nodeList.get(i));
}
nodeList.set(i, kn);
if (i == nodeList.size() / 2)
return;//The order of medians is completed, but not all of them. This termination condition only ensures that the median is correct. Removing this condition guarantees that all trees will be recursive.
//Sort all the numbers
else if (i < nodeList.size() / 2) {
quickSortForMedian(nodeList, index, i + 1, right);//Just sort the right side.
} else {
quickSortForMedian(nodeList, index, left, i - 1);//Just sort the left side.
}
// for (Node node : nodeList) {
// System.out.println(node.getData(index));
// }
}
}
Epilogue
Do this first, come back and change it later.