KNN(K-Nearest Neighbors) generally refers to K-nearest neighbor algorithm, which is a common classification algorithm in machine learning
The purpose of this paper is to quickly teach you an intuitive understanding of KNN algorithm. At the same time, in order to facilitate you to implement the algorithm, the model involved in this paper is developed only using Python and Numpy library

1 Introduction

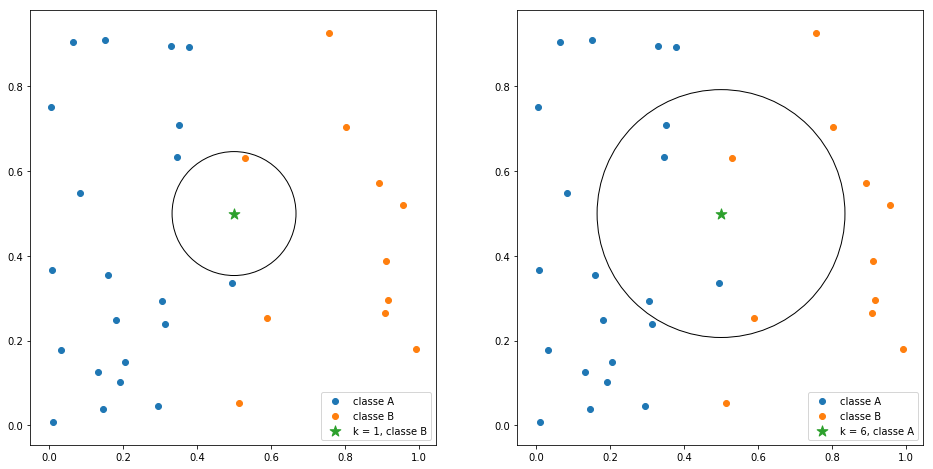
From the name of KNN, we can roughly understand the principle of the algorithm. The model uses the category of k neighbors to predict and classify the current sample. Here k represents the number of neighbor samples closest to the current sample in the feature space
If k=1, the category of the sample to be classified completely depends on the category of the nearest neighbor in the feature space
If k=n, the category of samples to be classified depends on the N nearest neighbors in the sample space. For the legend of the above two cases, please refer to the following figure:

2 distance measurement

By observing the above figure, some students will ask questions. How can we determine which points belong to the neighbors of the samples to be classified?
Here we introduce the dissimilarity measure of eigenvectors, which can refer to the previous Bowen.
In the above blog posts, many formulas for calculating the distance between eigenvectors are given, which will not be described here. I will use the simplest Euclidean distance for demonstration, and the calculation method is as follows:
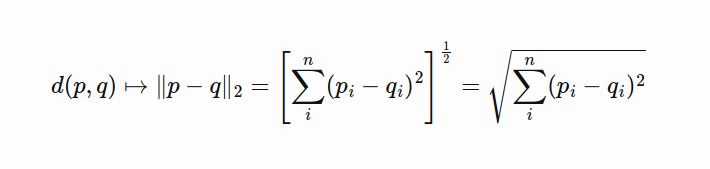The implementation code is as follows:

ldist = ['euclidian', 'manhattan', 'chebyshev', 'canberra', 'cosine']

class Distance(object):
  def __init__(self, metric='euclidian'):
    super(Distance, self).__init__()
    if metric not in ldist:
      raise ValueError('Metric does not exist! Choose between: {}'.format(ldist))
    self._metric = metric
  
  @property
  def metric(self):
    return self._metric
  
  @metric.setter
  def metric(self, m):
    if m not in ldist:
      raise ValueError('Metric does not exist! Choose between: {}'.format(ldist))
    self._metric = m
  
  def distance(self, p, q):
    return np.sum((p - q)**2, axis=1)**0.5

3 k-NN classification

KNN classification algorithm is very simple. The core idea of the algorithm is that if most of the k nearest samples in the feature space belong to a certain category, the sample also belongs to this category
In other words, the category of the sample to be classified is voted by the k nearest samples, and the category with the most votes is the category of the sample
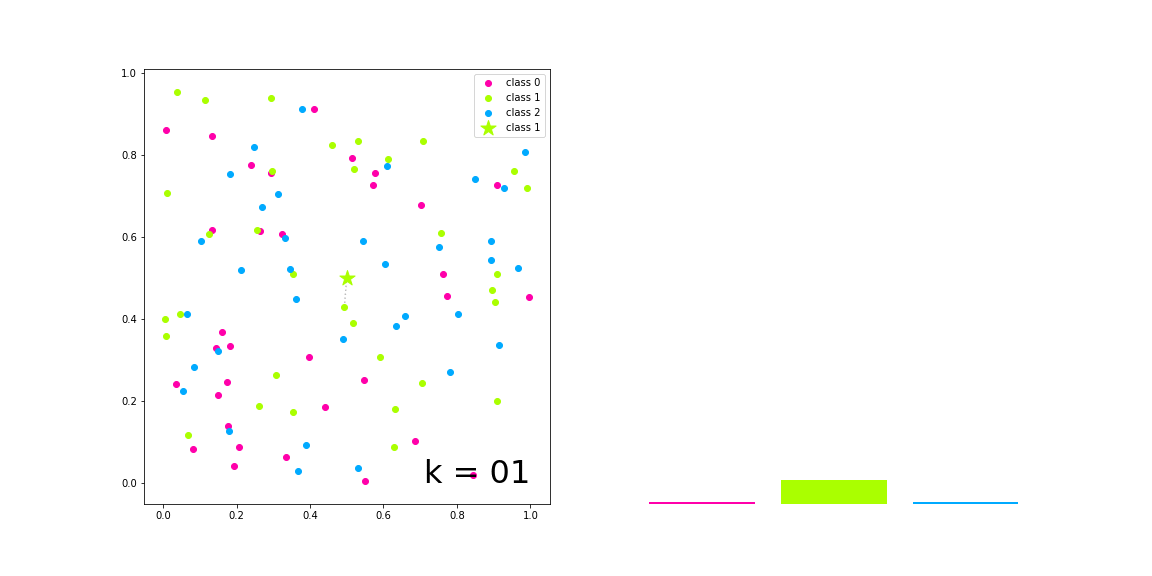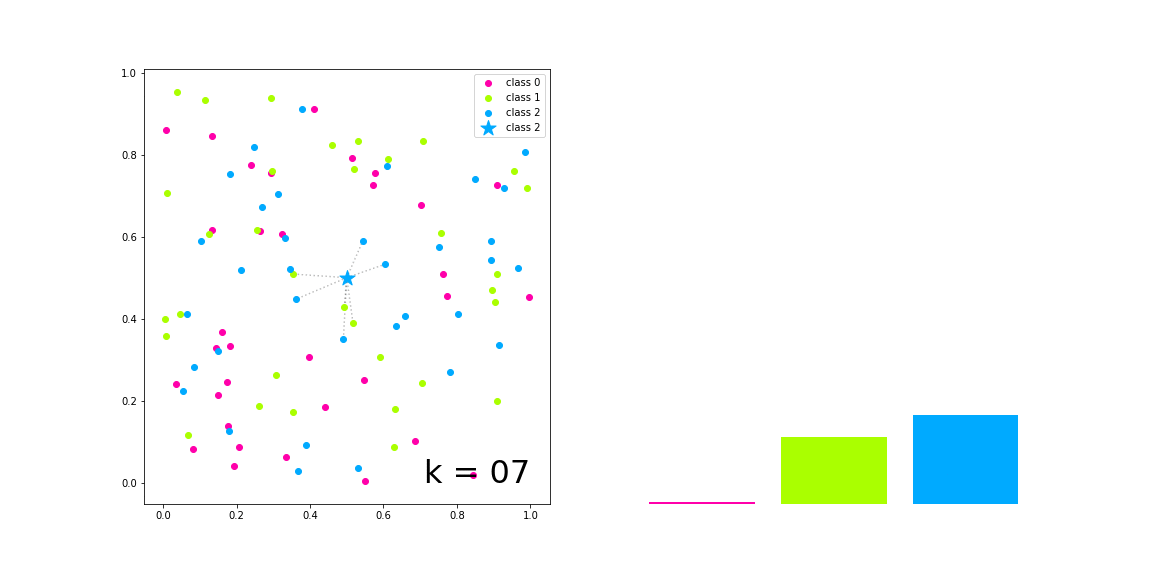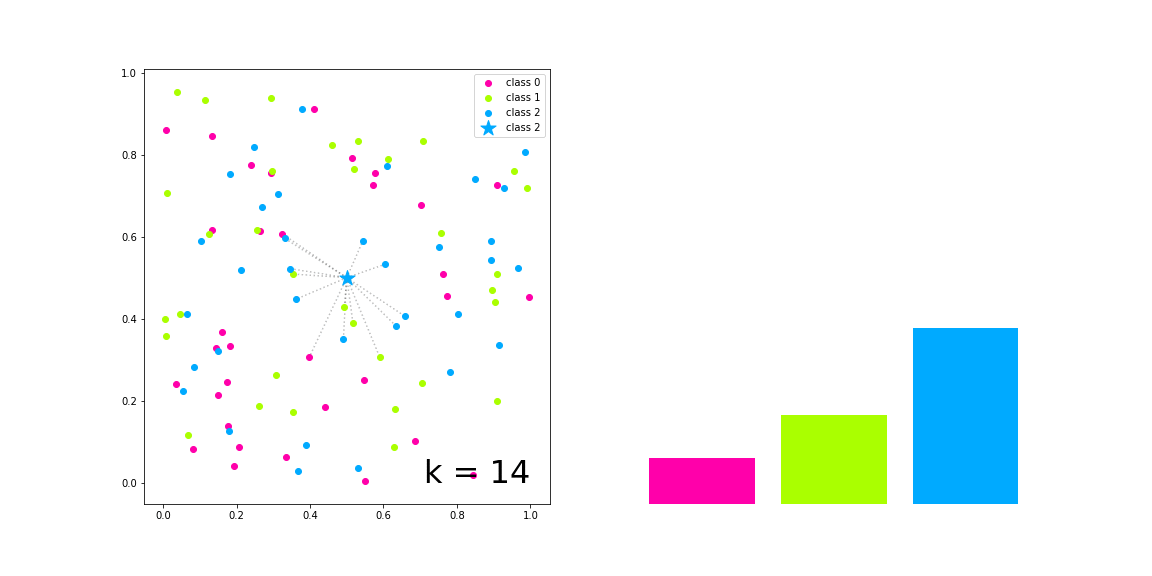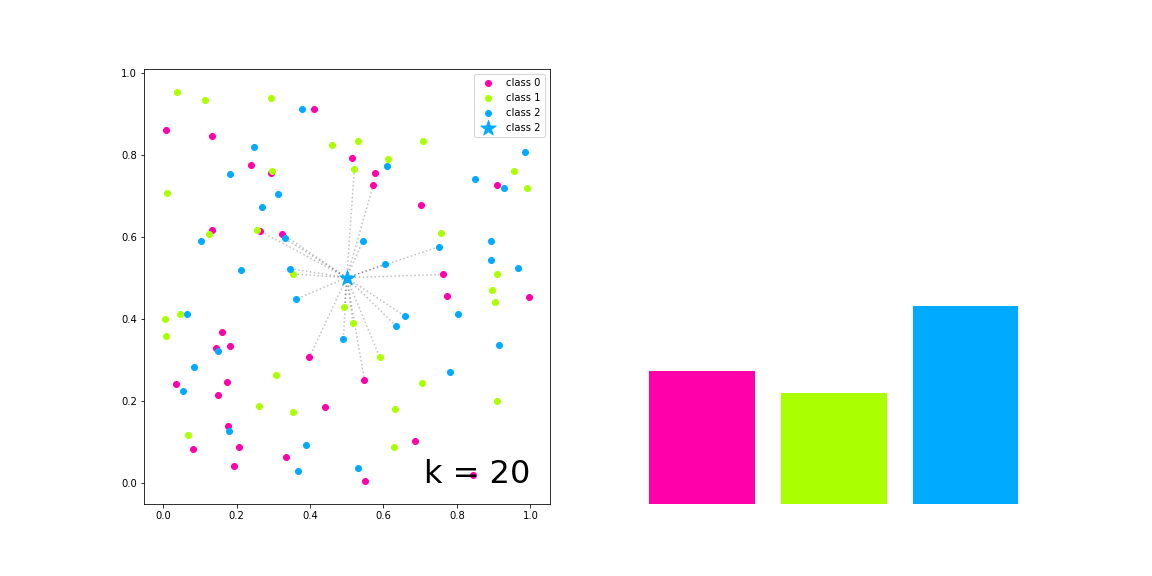In the figure on the left of the figure above, we have generated samples of three categories, which are represented by red, green and blue solid circles respectively, and the samples to be classified are represented by five pointed stars
With the increase of K value, the left side visualizes the k nearest neighbors of the sample to be classified and their voting results, and the right side represents the respective numbers of the three categories in the voting

The code implementation is as follows:

class kNNClass(Distance):
  def __init__(self, k=1):
    super(kNNClass, self).__init__()
    self._k = k
    self._q = None
    self._class = None
  
  def fit(self, X, y):
    self._q = X
    self._class = y
  
  def pred(self, P):
    y, NNs = [], []
    for i, p in enumerate(P):
      dist = self.distance(p, self._q)
      odist = np.argsort(dist)[:self._k]
      fdist = np.ravel(self._class[odist])
      hist = np.bincount(fdist)
      index = np.argmax(hist)
      y += [index]
      NNs += [odist]
    return np.array(y), np.array(NNs)

In the above code:

• The fit function is used to label the input x and assign it y
• The pred function uses KNN to predict the category of samples p to be classified

We use different k values to predict another set of data. The comparison diagram obtained by using different k values is as follows:
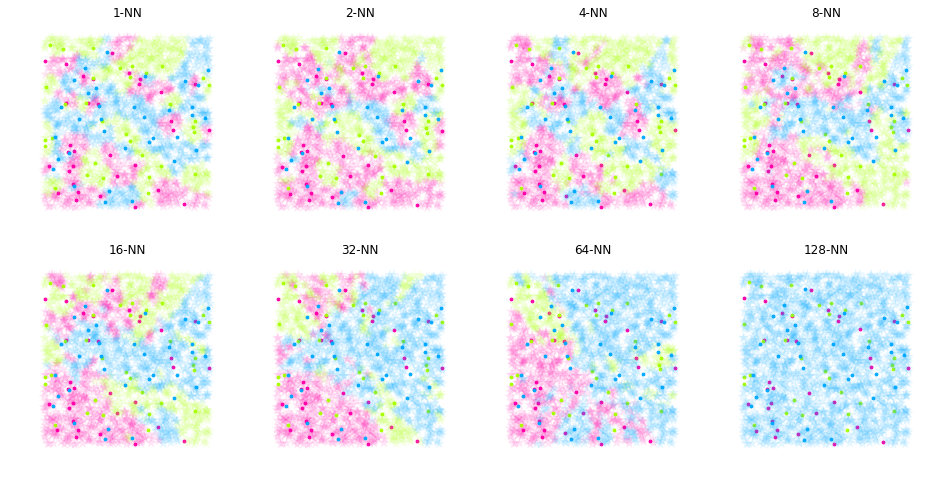The solid red, green and blue circles in the figure above represent the training samples we marked, and the five pointed stars represent the results of KNN voting

4 k-NN prediction

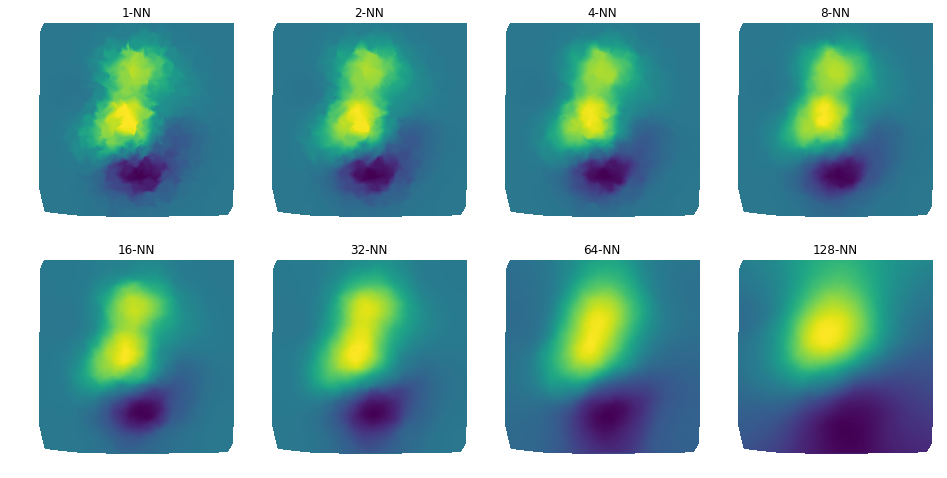
Similar to the classification algorithm, the KNN prediction process is to predict the value of the current sample according to the value of k neighbors. Here, similar to the general regression method, the distance weighted average of k neighbors is used to obtain the predicted value of the current sample
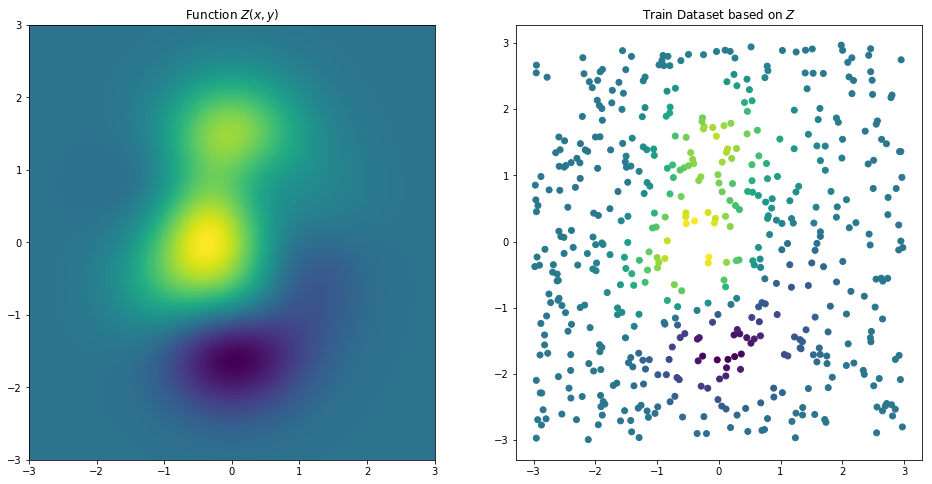Let's generate sample data. On the left is the thermodynamic diagram of the following binary function:
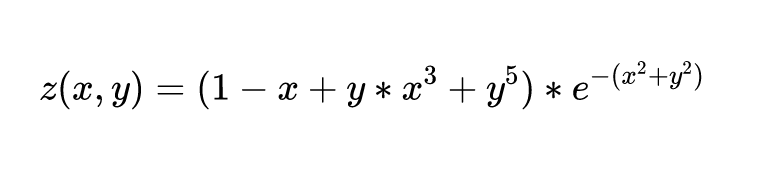We take uniform sampling points as our training samples, and the distribution of sampling points is shown on the right
We refer to the k-NN classification sample code to implement the prediction code, as shown below:

class kNNRegr(Distance):
  def __init__(self, k=1):
    super(kNNRegr, self).__init__()
    self._k = k
    self._q = None
    self._v = None
  
  def fit(self, X, y):
    self._q = X
    self._v = y
    
  def pred(self, P):
    y, NNs = [], []
    for i, p in enumerate(P):
      dist = self.distance(p, self._q)
      odist = np.argsort(dist)[:self._k]
      fdist = np.ravel(self._v[odist])
      ndist = dist[odist]
      ndist /= np.sum(ndist)
      y += [np.sum(fdist*np.flipud(ndist))]
      NNs += [odist]
    return np.array(y), np.array(NNs)

In the above code:

• The fit function is used to label the input x and assign it y
• The pred function uses KNN to predict the value of sample p to be predicted, where the calculation formula is distance weighting

The results are as follows:

5 Summary

This paper introduces the principle of k-NN classification and regression model in the field of machine learning and the corresponding code implementation, and gives a complete code example

Have you failed?

6 reference

reference resources Link one
Link 2

Pay attention to the official account of AI algorithm and get more AI algorithm information.

Note: complete code, official account, background reply KNN, you can get it.