k-free clustering method
Preface
It is well known that k-means clustering algorithm can only give unsupervised learning results under the given conditions of k. Simply speaking, it is necessary to know several categories in advance before clustering can be completed. Most of the time, we can not know or it is difficult to know how many classes there are in the specific data. Therefore, it is particularly important to find a clustering algorithm without given k conditions (i.e. without knowing how many classes there are).
Here I tentatively give a method that I think is feasible (I hope readers will discuss the correctness of this method with me).
Brief Analysis of Algorithms
First of all, we must give a restriction condition, which defines the maximum distance from the classification point in each group (in short, the mean point in k-mean s, or in a sense, the particle) to the group point.
With the above given premises, we can analyze the problem as follows:
Simple dichotomy:
1. First, consider whether the current data group can be used as a group, and if so, insert the group into the result group set. The criterion is to calculate the coordinates of the classification points first, then calculate the distances from each point to the classification points one by one, and compare whether the distances from all data points to the classification points are less than the given maximum distance, if so, it should be a feasible grouping, if not.
2. Dividing all data points by 2-means algorithm, two groups of data are obtained, and each group of data recursively calls this method (that is, iterating the two sets of data sets from step 1 respectively).
3. Output result grouping set.
Preliminary explanation:
Since any non-negative integer can be represented by binary, all possible groupings can be guaranteed. The above process is actually a binary representation process, we can pass it as a binary tree, and its classification is the number of leaf nodes, as shown in Figure 1.
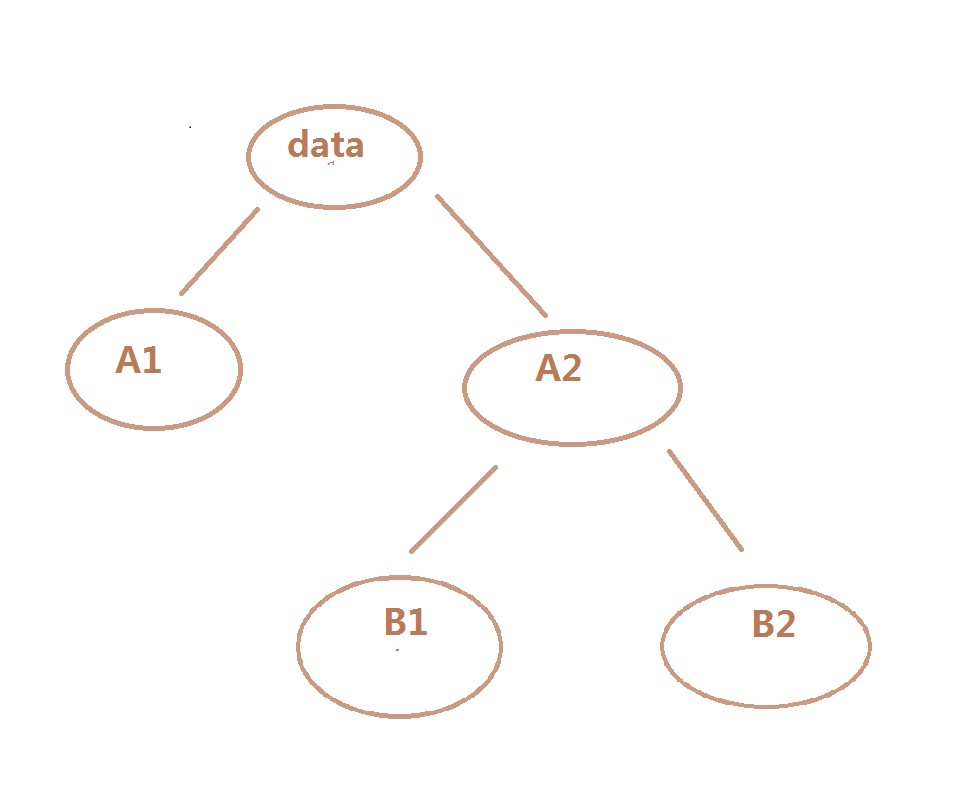
Figure 1
It is clear that the first iteration divides the data set into two groups, and then the former group (A1) is retained as one of the result sets because it has reached the standard, while the latter group (A2) still needs to be iterated because it still does not meet the requirements. The latter iteration divides the data set into two eligible feasible groups (B1,B2).
At the end of the iteration, the result set ({A1,B1,B2}) is output.
Parallel optimization:
After obtaining the above result set, we will find that some groups can be merged into one group, but because of the above, they correspond to two groups respectively, as shown in Figure 2 below.
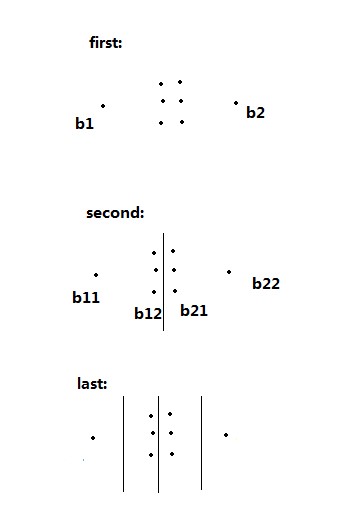
Figure 2
Here we should have put the middle two groups as a group, but because of the random selection of the initial iteration point, it will lead to the phenomenon of over-grouping as mentioned above. To solve the above phenomenon, I made an optimization, and its idea is waiting for me to speak slowly.
First, we try to merge the groupings in the above result sets. Arbitrarily take two result sets for the following operations.
1. To determine whether there are two groupings that can be merged in the result set (i.e., the two groupings can still meet the maximum distance requirement after merging into one), if there are, turn to 2, if not, output the result, and the algorithm terminates.
2. Combine the two groups S1. and S2 into one group S, replace S1 and S2 with S, and update the result set to 1.
After completing this task, we have solved the above problems. We are very happy to get the following results, as shown in Figure 3.
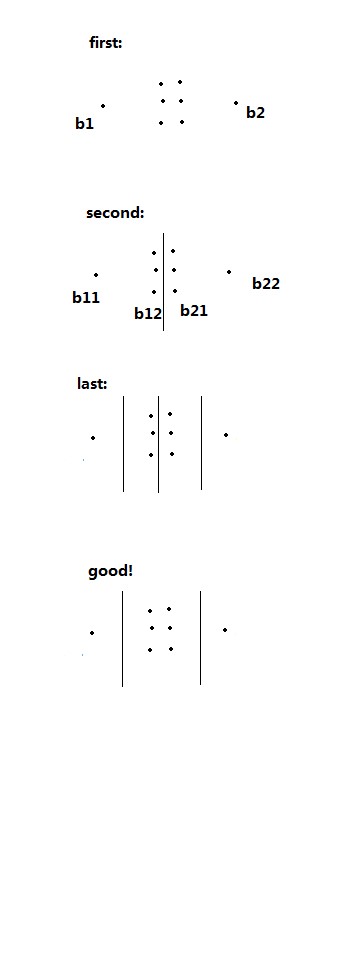
Figure 3
Ha ha ha! Not finished yet? Optimizing continues...
Group optimization:
Here's the question: Can some groups be disassembled as part of others? In this way, the group no longer exists as part of other groups, which can also reduce the number of groups.
Based on this idea, we derive such an algorithm:
1) Judging whether there is a grouping that can be completely disassembled as part of other groupings (this judgment is slightly complicated. What you need to do is not just to try to put every element into other groupings, but also to consider that the whole result set changes when an element is put into another grouping, and the grouping point that should be put into the grouping also changes. It is meaningless that each element of each group belongs to other groups independently. This is a dynamic problem, which can not be considered statically. If not, the result will be output. If there is a turn 2.
2) Unfold the group, place it in other groups of the result set in turn, and delete the group from the result set. Turn 1.
The phenomena are roughly as shown in Figure 4 below.
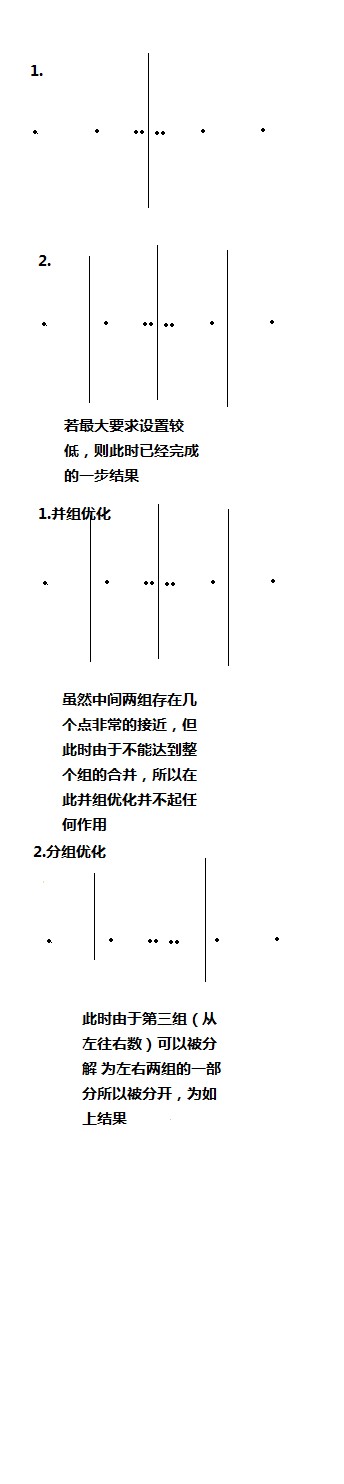
The experimental code and results are as follows:
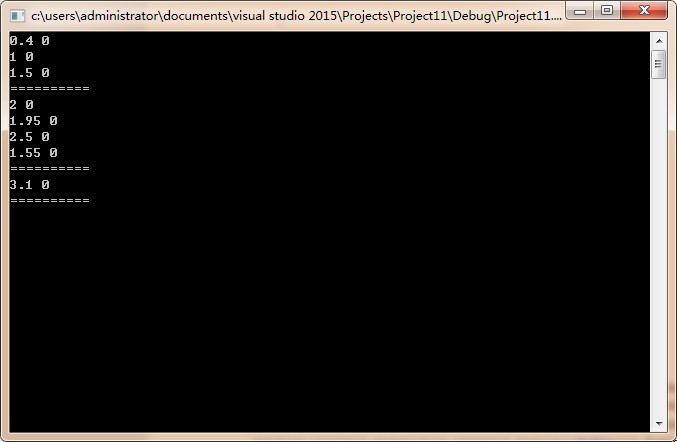
The experimental data are as follows:
{{0.4,0},{1,0},{2.5,0},{3.1,0},{1.5,0},{ 1.55,0 },{2,0},{1.95,0}}
#include <iostream>
#include <string>
#include <cstring>
#include <fstream>
#include <functional>
#include <algorithm>
#include <ctime>
#include <cmath>
#include <vector>
#include <limits>
#include <unordered_set>
#include <memory>
using namespace std;
const double eps = 0.00001;
unordered_set<shared_ptr<vector<double>>> tos;
unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>> midres;
unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>> realres;
unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>> nextres;
unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>> finalres;
double stddis;
double maxdis(const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &s, shared_ptr<vector<double>> &p1, shared_ptr<vector<double>> &p2);
double dis(const shared_ptr<vector<double>> &p1, const shared_ptr<vector<double>> &p2);
shared_ptr<vector<double>> getmid(shared_ptr<unordered_set<shared_ptr<vector<double>>>> s);
double nrom(const shared_ptr<vector<double>> &p);
shared_ptr<vector<double>> operator-(const shared_ptr<vector<double>> &p);
shared_ptr<vector<double>> operator+(const shared_ptr<vector<double>> &p1, const shared_ptr<vector<double>> &p2);
shared_ptr<vector<double>> operator-(const shared_ptr<vector<double>> &p1, const shared_ptr<vector<double>> &p2);
ostream& operator<<(ostream& o, const shared_ptr<vector<double>> &p);
void get2(const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &s);
bool getClass();
double dis(const shared_ptr<vector<double>> &p1, const shared_ptr<vector<double>> &p2) {
double res = 0;
for (int i = 0; i < p1->size(); ++i) {
res += ((*p1)[i] - (*p2)[i])*((*p1)[i] - (*p2)[i]);
}
return sqrt(res);
}
double maxdis(const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &s, shared_ptr<vector<double>> &p1, shared_ptr<vector<double>> &p2) {
double mmax = 0;
double res = 0;
shared_ptr<vector<double>> mid = getmid(s);
for (shared_ptr<vector<double>> pv : *s) {
for (shared_ptr<vector<double>> pn : *s) {
double tem = dis(pv, pn);
if (tem > mmax) {
mmax = tem;
p1 = pv;
p2 = pn;
}
}
res = max(res, dis(mid, pv));
}
return res;
}
shared_ptr<vector<double>> getmid(shared_ptr<unordered_set<shared_ptr<vector<double>>>> s) {
shared_ptr<vector<double>> res = shared_ptr<vector<double>>(new vector<double>((*(s->begin()))->size()));
for (const shared_ptr<vector<double>> &p : *s) {
for (int i = 0; i < p->size(); ++i) {
(*res)[i] += (*p)[i]/s->size();
}
}
return res;
}
double nrom(const shared_ptr<vector<double>> &p) {
double res = 0;
for (double td : *p) {
res += td*td;
}
return sqrt(res);
}
shared_ptr<vector<double>> operator-(const shared_ptr<vector<double>> &p) {
shared_ptr<vector<double>> res = shared_ptr<vector<double>>(new vector<double>(p->size()));
for (int i = 0; i < p->size(); ++i) {
(*res)[i] = -(*p)[i];
}
return res;
}
shared_ptr<vector<double>> operator+(const shared_ptr<vector<double>> &p1, const shared_ptr<vector<double>> &p2) {
if (p1->size() != p2->size())
return nullptr;
shared_ptr<vector<double>> res = shared_ptr<vector<double>>(new vector<double>(p1->size()));
for (int i = 0; i < p1->size(); ++i) {
(*res)[i] = (*p1)[i]+ (*p2)[i];
}
return res;
}
shared_ptr<vector<double>> operator-(const shared_ptr<vector<double>> &p1, const shared_ptr<vector<double>> &p2) {
return p1 + (-p2);
}
ostream& operator<<(ostream& o, const shared_ptr<vector<double>> &p) {
for (double td : *p) {
o << td << " ";
}
return o;
}
void get2(const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &s) {
shared_ptr<vector<double>> p1;
shared_ptr<vector<double>> p2;
if (maxdis(s,p1,p2) <= stddis) {
midres.insert(s);
return;
}
shared_ptr<unordered_set<shared_ptr<vector<double>>>> s1 = shared_ptr<unordered_set<shared_ptr<vector<double>>>>(new unordered_set<shared_ptr<vector<double>>>());
shared_ptr<unordered_set<shared_ptr<vector<double>>>> s2 = shared_ptr<unordered_set<shared_ptr<vector<double>>>>(new unordered_set<shared_ptr<vector<double>>>());
for (shared_ptr<vector<double>> p : *s) {
if (dis(p, p1) < dis(p, p2)) {
s1->insert(p);
}
else {
s2->insert(p);
}
}
shared_ptr<vector<double>> np1 = getmid(s1);
shared_ptr<vector<double>> np2 = getmid(s2);
while (nrom(np1 - p1) > eps || nrom(np2 - p2) > eps) {
s1->clear();
s2->clear();
for (shared_ptr<vector<double>> p : *s) {
if (dis(p, p1) < dis(p, p2)) {
s1->insert(p);
}
else {
s2->insert(p);
}
}
p1 = np1;
p2 = np2;
shared_ptr<vector<double>> np1 = getmid(s1);
shared_ptr<vector<double>> np2 = getmid(s2);
}
get2(s1);
get2(s2);
}
bool isSum(const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &ps, const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &psn, shared_ptr<unordered_set<shared_ptr<vector<double>>>> &outping, shared_ptr<unordered_set<shared_ptr<vector<double>>>> &outfloat) {
shared_ptr<unordered_set<shared_ptr<vector<double>>>> tempres = shared_ptr<unordered_set<shared_ptr<vector<double>>>>(new unordered_set<shared_ptr<vector<double>>>(*ps));
tempres->insert(psn->begin(), psn->end());
shared_ptr<vector<double>> mid = getmid(tempres);
bool flag = true;
for (shared_ptr<vector<double>> ptd : *tempres) {
if (dis(ptd, mid) > stddis) {
outfloat->insert(ptd);
flag = false;
}
else {
outping->insert(ptd);
}
}
return flag;
}
int pingClass(const shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>> &s) {
shared_ptr<unordered_set<shared_ptr<vector<double>>>> floatTemp = nullptr;
shared_ptr<unordered_set<shared_ptr<vector<double>>>> pingTemp = nullptr;
shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>> tempres = shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>>(new unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>(*s));
shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>> firstout = shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>>(new unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>());
while (!tempres->empty()) {
bool flag = false;
shared_ptr<unordered_set<shared_ptr<vector<double>>>> spt = *(tempres->begin());
for (const shared_ptr<unordered_set<shared_ptr<vector<double>>>> sptn : *tempres) {
if (spt == sptn)
continue;
floatTemp = shared_ptr<unordered_set<shared_ptr<vector<double>>>>(new unordered_set<shared_ptr<vector<double>>>());
pingTemp = shared_ptr<unordered_set<shared_ptr<vector<double>>>>(new unordered_set<shared_ptr<vector<double>>>());
if (isSum(spt, sptn, pingTemp, floatTemp)) {
spt->insert(sptn->begin(), sptn->end());
tempres->erase(sptn);
flag = true;
break;
}
}
if (!flag) {
tempres->erase(spt);
firstout->insert(spt);
}
}
nextres = *firstout;
return nextres.size();
}
bool add(const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &ps, const shared_ptr<vector<double>>& pd) {
ps->insert(pd);
shared_ptr<vector<double>> mid = getmid(ps);
for (shared_ptr<vector<double>> ptd : *ps) {
if (dis(ptd, mid) > stddis) {
ps->erase(pd);
return false;
}
}
return true;
}
bool openClass(shared_ptr<unordered_set<shared_ptr<vector<double>>>> pt,shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>> &s) {
shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>> b = shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>>(new unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>());
for (shared_ptr<unordered_set<shared_ptr<vector<double>>>> apt : *s) {
shared_ptr<unordered_set<shared_ptr<vector<double>>>> tpt(new unordered_set<shared_ptr<vector<double>>>(*apt));
if (apt == pt) {
pt = tpt;
}
b->insert(shared_ptr<unordered_set<shared_ptr<vector<double>>>>(tpt));
}
b->erase(pt);
while (!pt->empty()){
shared_ptr<vector<double>> nowpt = *(pt->begin());
bool flag = false;
for (const shared_ptr<unordered_set<shared_ptr<vector<double>>>> &ptd : *b) {
if (add(ptd,nowpt)) {
flag = true;
break;
}
}
if (flag) {
pt->erase(nowpt);
}
else {
return false;
}
}
s = b;
return true;
}
void deepPingClass(shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>> s) {
while (true) {
bool flag = false;
for (shared_ptr<unordered_set<shared_ptr<vector<double>>>> pt : *s) {
if (openClass(pt, s)) {
flag = true;
break;
}
}
if (!flag) {
break;
}
}
finalres = *s;
}
bool getClass() {
get2(shared_ptr<unordered_set<shared_ptr<vector<double>>>>(new unordered_set<shared_ptr<vector<double>>>(tos)));
pingClass(shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>>(new unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>(midres)));
deepPingClass(shared_ptr<unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>>(new unordered_set<shared_ptr<unordered_set<shared_ptr<vector<double>>>>>(nextres)));
return false;
}
int main() {
vector<vector<double>> solve = { {0.4,0},{1,0},{2.5,0},{3.1,0} ,{1.5,0},{ 1.55,0 },{2,0},{1.95,0} };
for (const vector<double> & v : solve) {
tos.insert(shared_ptr<vector<double>>(new vector<double>(v)));
}
stddis = 0.6;
getClass();
for (shared_ptr<unordered_set<shared_ptr<vector<double>>>> p : finalres) {
for(shared_ptr<vector<double>> pv:*p) {
for (double i : *pv) {
cout << i << " ";
}
cout << endl;
}
cout << "==========" <<endl;
}
cin >> stddis;
return 0;
}