Relevant introduction:
_The search efficiency of binary search tree is related to the shape of binary tree. If the left and right subtrees of a binary sort tree are evenly distributed, the search process is similar to the binary search of an ordered table, and the time complexity becomes O(log2n). If the given sequence is in order, the binary search tree will be transformed into a single linked list, and its search efficiency is the same as that of sequential search, and the time complexity is O (n). Therefore, in the process of constructing binary search tree, when the distribution of left and right subtrees is not uniform, if it can be adjusted to keep it uniform, it can effectively ensure that the binary search tree still has high search efficiency. The balanced binary tree is just such a tree.
Equilibrium binary tree, also known as AVL tree, is either an empty tree or a binary tree with the following properties: its left subtree and right subtree are balanced binary trees, and the absolute value of the difference between the depth of left subtree and right subtree does not exceed 1.
After inserting or deleting nodes in the balanced binary tree, the binary tree may lose its balance. Therefore, it is necessary to adjust the unbalanced binary tree to maintain the nature of the balanced binary tree. Following, we mainly introduce how to balance a binary search tree dynamically, that is, to balance the unbalanced binary search tree. The concept of equilibrium factor is introduced here.
The so-called balance factor refers to the difference between the left subtree depth and the right subtree depth of a node in a binary tree. The balance factor is also called the balance degree. Equilibrium binary tree is a binary tree whose absolute value of equilibrium factor of any node in the tree is less than or equal to 1. The equilibrium factor of nodes in AVL tree has three values: 1 (left subtree depth is greater than right subtree depth), 0 (left subtree depth is equal to right subtree depth), and - 1 (left subtree depth is less than right subtree depth).
In the example given below, for the sake of convenience, it is assumed that the root node of the smallest subtree which is out of balance due to inserting new nodes in the AVL tree is A, that is, A is the nearest node to the inserting node, and the equilibrium factor is not - 1, 0 and 1. The operation after losing balance can be summarized into the following four situations according to the reasons for losing balance (a key to the recipe for easy memory, such as "LL-type balanced rotation", which refers to the imbalance problem caused by inserting a new node into the left child node (L) of A's left child node (L):
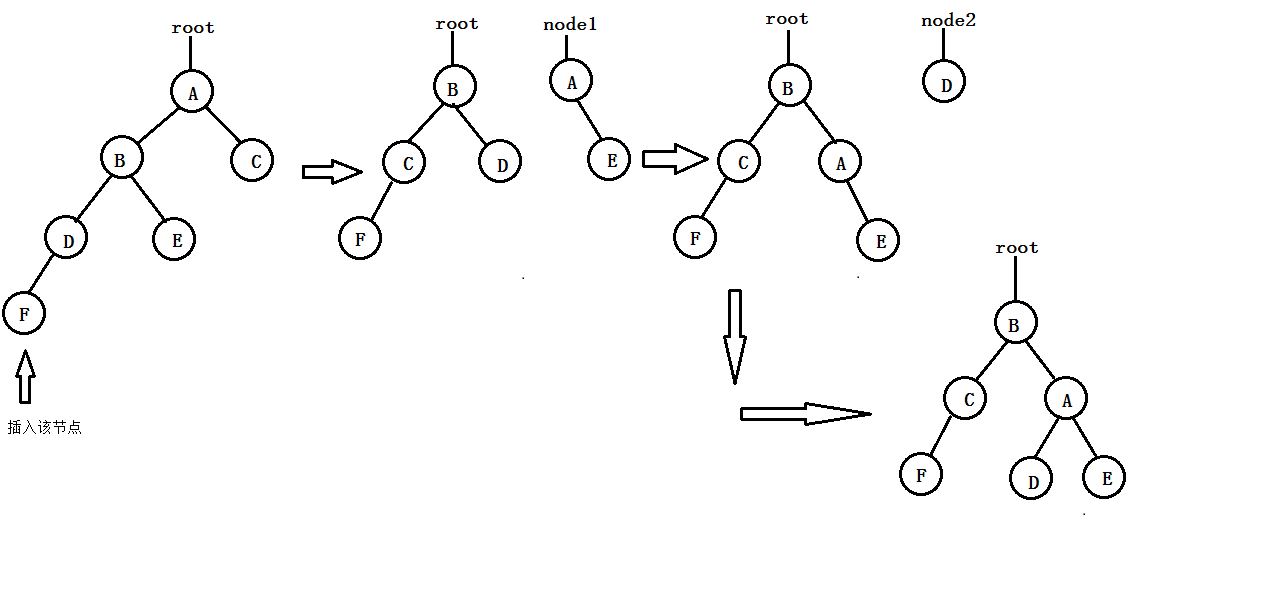
- LL-type balanced rotation (one-way right-handed): As a result of inserting new nodes into the left subtree of A's left child, the balance degree of A increases from 1 to 2, resulting in the unbalance of the subtree rooted in A. At this time, a clockwise rotation operation should be performed to the right, and "lifting" B (that is, the left child of A) is the root node of the new subtree, and A falls to the right child of B. At the same time, the original right subtree B-R of B is adjusted to the left subtree of A. The process is shown in the following figure:
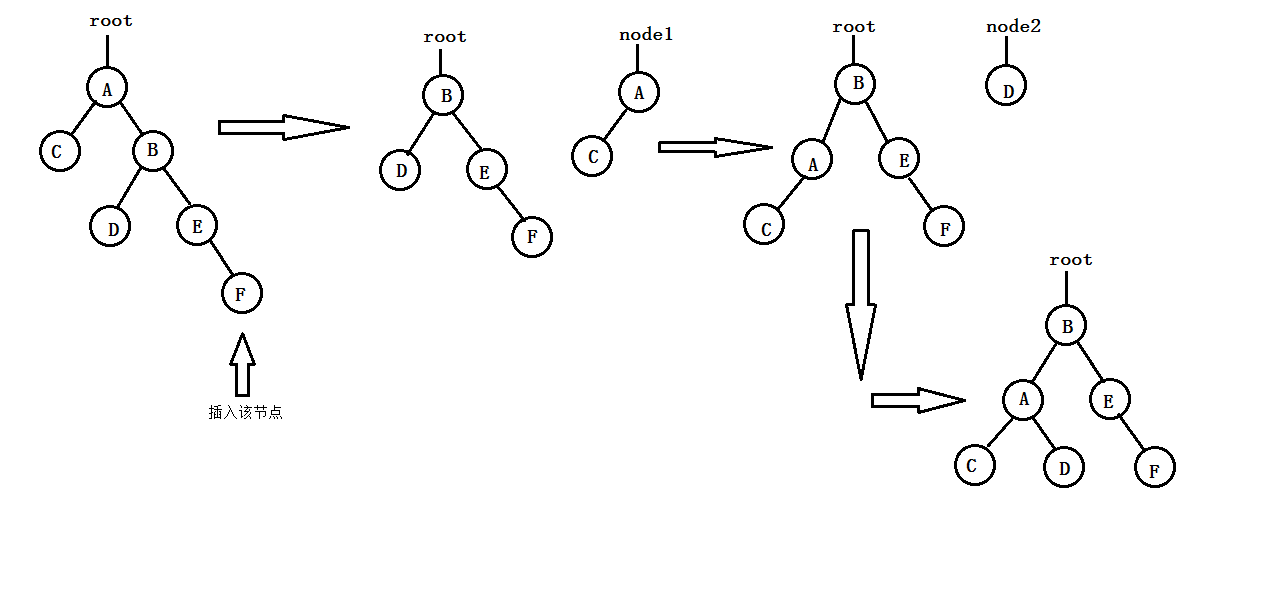
- RR-type balanced rotation (one-way left-handed): As a result of inserting new nodes into the right subtree of A's right child, the balance degree of A changes from - 1 to - 2, resulting in the unbalance of the subtree rooted in A. At this time, we should do a left counter-clockwise rotation operation, "lifting" B (that is, the right child of A) as the root node of the new subtree, A falling to the left subtree of B, and adjusting the original left subtree B-L of B to the right subtree of A. The process is shown in the following figure:
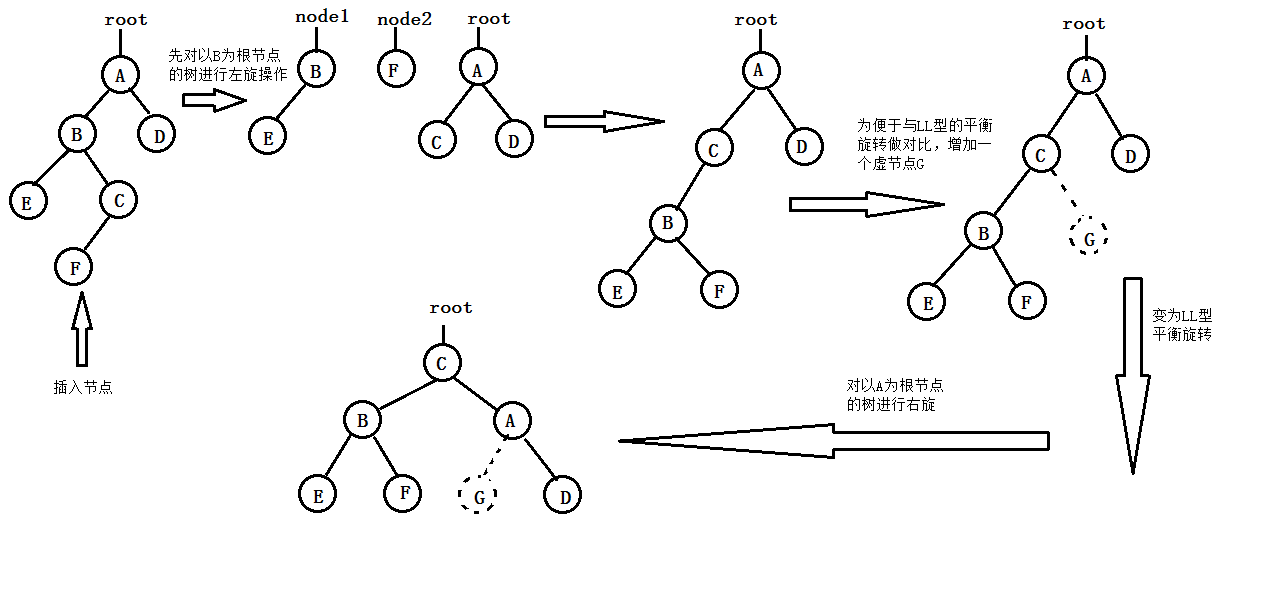
- LR-type balanced rotation (first left-handed and then right-handed): As a result of inserting new nodes into the right subtree of A's left child, the balance degree of A changes from 1 to 2, resulting in the unbalance of the subtree rooted in A. At this time, two selection operations (first counterclockwise, then clockwise) should be carried out to "elevate" C (that is, the right child of A's left child) to the root node of the new subtree; A to the right child of C; B to the left child of C; C to the right subtree of B; C to the left subtree of A. The process is shown in the following figure:
or
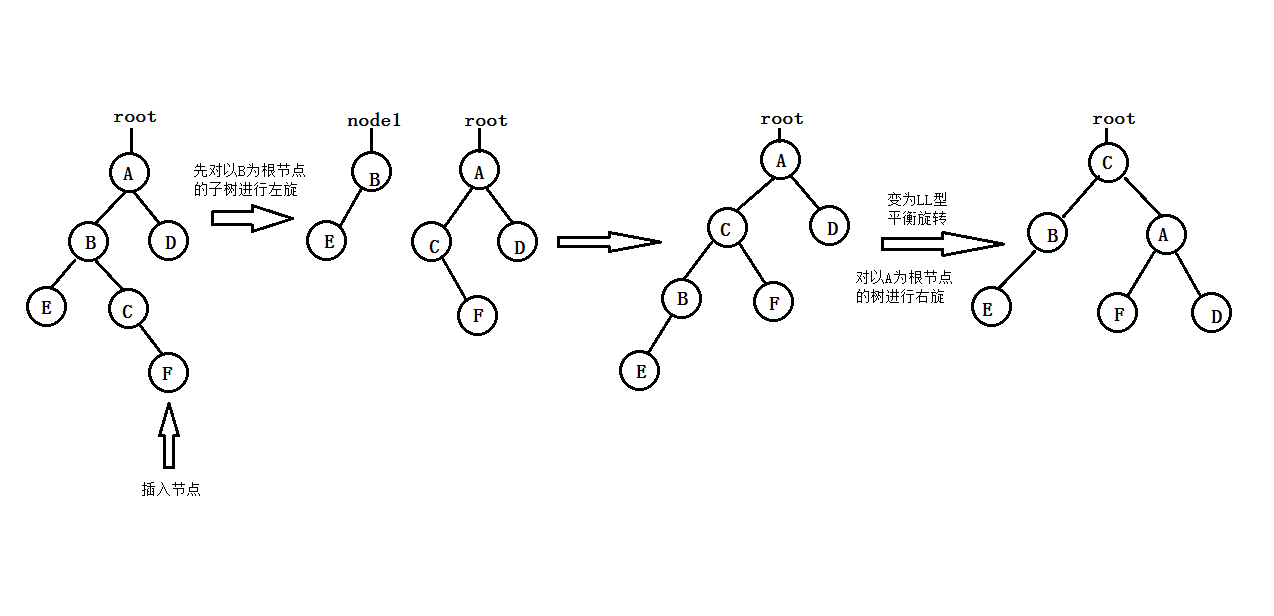
- RL-type balanced rotation (first right-handed and then left-handed): As a result of inserting new nodes into the left subtree of A's right child, the balance degree of A changes from - 1 to - 2, resulting in the unbalance of the subtree with A as its root. At this time, two rotation operations (first clockwise, then counterclockwise) should be carried out, and "elevation" C (that is, the left child of A's right child) is the root node of the new subtree; A decreases to the left child of C; It is the right child of C; the left subtree C-L of C is adjusted to the right subtree of A; the right subtree C-R of C is adjusted to the left subtree of B. The process is shown in the following figure:
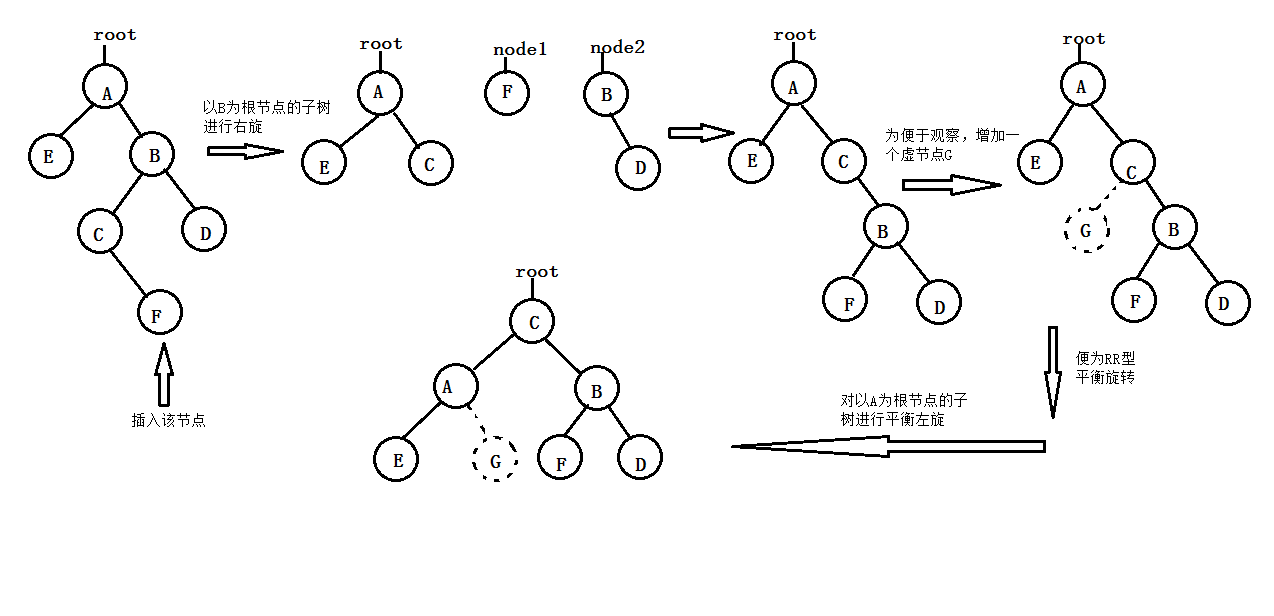
or
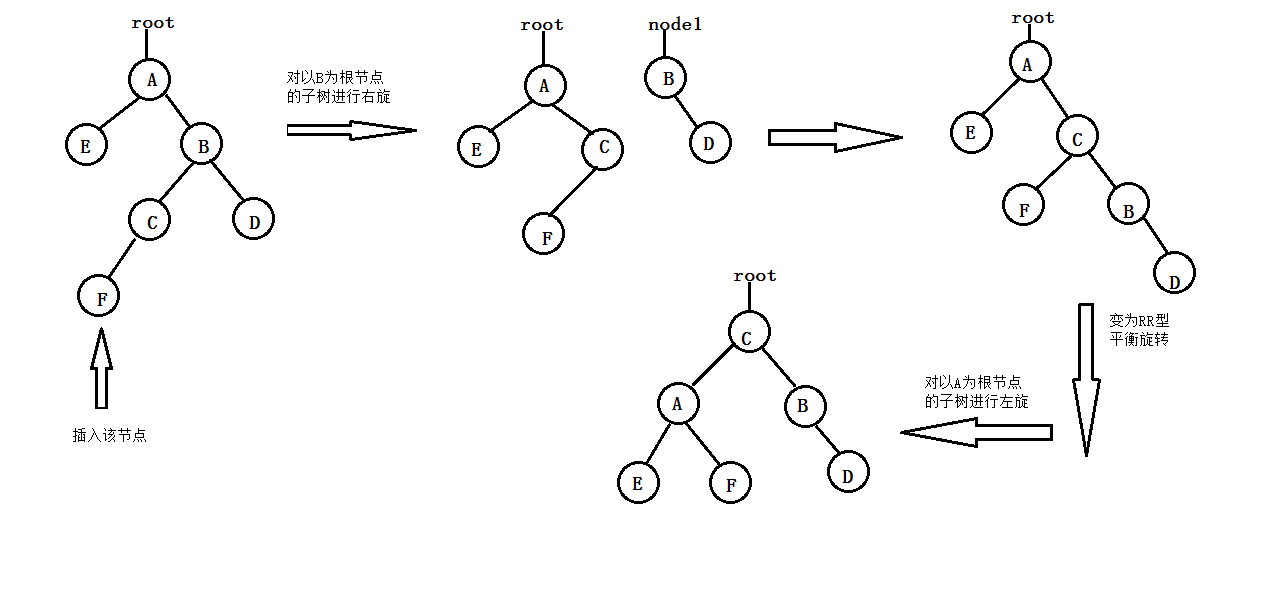
To sum up, the algorithm of inserting a new record x into the balanced binary search tree T is described as follows:
- If the AVL tree is empty, a new node recorded as x is inserted as the root node of T, and the depth of the tree is increased by 1.
- If the keyword value of x is equal to the keyword value of the root node of AVL tree T, the insertion operation is not performed.
-
If the key value of X is less than the key value of the root node of AVL tree, then x is inserted into the left subtree of AVL tree. When the depth of the left subtree increases by 1, the following different situations are dealt with respectively:
If the equilibrium factor of the root node of AVL tree is -1 (the depth of the right subtree is greater than that of the left subtree), then the equilibrium factor of the root node is adjusted to 0, and the depth of the tree remains unchanged.
If the equilibrium factor of the root node of the AVL tree is 0 (the depth of the left and right subtrees is equal). Then the equilibrium factor of the root node is adjusted to 1, and the depth of the tree is increased by 1 at the same time.
If the equilibrium factor of the root node of AVL tree is 1 (the depth of the left subtree is greater than the depth of the right subtree), LL-type equilibrium rotation is needed when the equilibrium factor of the root node of the left subtree is 1; LR-type equilibrium rotation is needed when the equilibrium factor of the root node of the left subtree of AVL tree is -1.
-
If the key value of X is greater than the key value of the root node of AVL tree, then x is inserted into the right subtree of AVL tree. When the depth of the right subtree increases by 1, the following different situations are dealt with respectively:
- If the equilibrium factor of the root node of AVL tree is -1 (the depth of the right subtree is greater than the depth of the left subtree), then RR-type equilibrium rotation is needed when the equilibrium factor of the root node of the right subtree is -1; RL-type equilibrium rotation is needed when the equilibrium factor of the root node of the right subtree of AVL tree is 1.
2. If the equilibrium factor of the root node of AVL tree is 0 (the depth of the left and right subtrees is equal), then the equilibrium factor of the root node is adjusted to -1, and the depth of the tree is increased by 1 at the same time.
- If the equilibrium factor of the root node of AVL tree is 1 (the depth of the left subtree is greater than that of the right subtree), then the equilibrium factor of the root node is adjusted to 0, and the depth of the tree remains unchanged.
Advantages and disadvantages of balanced binary tree:
Advantages: It makes the structure of binary tree better (that is, there will be no "deflection" serious situation), thus improving the speed of search operation.
Disadvantage: Complex insertion and deletion operations, thus reducing the speed of insertion and deletion operations.
Summary: Balanced binary tree is suitable for applications where binary search tree seldom inserts or deletes once it is established, but mainly searches. Because the number of keywords that are compared with a given value in the search process does not exceed the depth of the tree. Therefore, the time complexity of searching on the balanced binary tree is O (log2n).
Sample code for related operations:
For balanced binary tree, the common operations are insertion, deletion and search. When inserting and deleting a node, it is necessary to rotate the unbalanced balanced binary search tree to keep its structure stable.
The following code defines the nodes of the balanced binary lookup tree:
Related codes:
/**
* This class is used to define the relevant data of the nodes of the balanced binary tree.
* @author Apprentice
*
*/
class AVLTreeNode
{
//Key words of nodes
Comparable key;
//Node data
Object data;
//Left subtree pointer of node
AVLTreeNode left;
//Right subtree pointer of node
AVLTreeNode right;
public AVLTreeNode(Comparable key,Object data)
{
this(key,data,null,null);
}
public AVLTreeNode(Comparable key,Object data,AVLTreeNode left,AVLTreeNode right)
{
this.data=data;
this.key=key;
this.left=left;
this.right=right;
}
}_For the lookup operation, it first compares with the value of the keyword of the root node. According to the results of the comparison, it chooses to return its relevant data or to search recursively in the left and right subtrees of the node.
The following code demonstrates the operation of lookup:
Related codes:
/**
* Used to balance the search operation in the binary tree, and return the relevant data of the corresponding node, when not found, return null
* @param key Keyword for the node to be looked up
* @return Get the relevant data for the node to be looked up
*/
public Object search(Comparable key)
{
if(key==null)
return null;
return getSearchResult(root,key);
}
/**
* Used to assist the balanced binary tree lookup operation, and return the data of the relevant nodes, when not found, return null
* @param root The root node of the binary search tree for lookup
* @param key Keyword for the node to be looked up
* @return Get the relevant data for the node to be looked up
*/
private Object getSearchResult(AVLTreeNode root,Comparable key)
{
if(root==null)
return null;
int compare=key.compareTo(root.key);
if(compare==0)
return root.data;
else if(compare==1)
return getSearchResult(root.right,key);
else
return getSearchResult(root.left,key);
}_For the insertion operation, the corresponding nodes are inserted into the balanced binary tree according to the size of the key words. After that, we traverse the equilibrium factors of each root node in the path of the new insertion node, and selectively rotate it according to the value of the equilibrium factors. It should be noted that there is only one "imbalance" in the path at most. Therefore, after rotating the nodes on its path, the balanced binary tree is in a "balanced" state as a whole.
The following code demonstrates the insertion operation:
Related codes:
/**
* Used to insert new nodes into a binary tree
* @param key Key words of new nodes in binary tree
* @param data Data of New Nodes in Binary Tree
* @return The result of inserting a new node returns true if it succeeds in inserting a new node, false if it does not, and false if the new node exists in the tree.
*/
public boolean insert(Comparable key,Object data)
{
if(key==null)
return false;
else if(root!=null)
{
return insertAVLTreeNode(root,null,key,data);
}
else
{
root=new AVLTreeNode(key,data);
return true;
}
}
/**
* Assist in inserting new nodes into the binary tree
* @param node Nodes of binary trees to be compared
* @param parent The parent node of the node of the binary tree to be compared
* @param key Key Value of New Node
* @param data Data of new nodes
* @return Additional results
*/
private boolean insertAVLTreeNode(AVLTreeNode node,AVLTreeNode parent,Comparable key,Object data)
{
//When the current comparison node is not empty, the comparison operation is performed
if(node!=null)
{
int compare=key.compareTo(node.key);
if(compare==0)
return false;
else if(compare>0)
return insertAVLTreeNode(node.right,node,key,data);
else
return insertAVLTreeNode(node.left,node,key,data);
}
//When the current node is empty, insert the node from its parent node. At the same time, the rotation judgement and corresponding operation are carried out.
else
{
Comparable parentKey=parent.key;
AVLTreeNode newNode=new AVLTreeNode(key,data);
int comparable=parentKey.compareTo(key);
//Insert new nodes
if(comparable>0)
parent.left=newNode;
else
parent.right=newNode;
//The nodes after insertion are judged to see if they need to rotate. When necessary, the nodes of the balanced binary tree are rotated and adjusted.
rotate(root,null,newNode);
return true;
}
}
For deletion operations, only the parent node of the node to be deleted needs to be found in the binary tree. After that, the corresponding pointer can be moved to delete the node, and it can be supplemented by successor nodes ordered by keywords. Then, all the nodes on the path from the parent node to the parent node to delete the node are traversed. When the deletion of the node results in its unbalanced situation, the corresponding balanced rotation operation is carried out.
The following code demonstrates the deletion operation:
Related codes:
/**
* Used for deletion operations
* @param key Keyword values of nodes to be deleted
* @return Returns the data value of the deleted node and null when there is no associated deleted node
*/
public Object delete(Comparable key)
{
if(key==null)
return null;
else
return remove(root,key,null);
}
/**
* A method for assisting with deletion operations
* @param node Current comparison node
* @param parent Parent Node of Current Compare Node
* @param key Keyword values of nodes that need to be deleted
* @return Returns the keyword of the deleted node
*/
public Object remove(AVLTreeNode node,Comparable key,AVLTreeNode parent)
{
if (node != null)
{
int compare = key.compareTo(node.key);
// Delete from the left subtree
if (compare < 0)
{
return remove(node.left, key, node);
}
// Delete from the right subtree
else if (compare > 0)
{
return remove(node.right, key, node);
}
// The current node is the node to be deleted
else
{
// Data of the node currently to be deleted
Object result = node.data;
// The left and right subtrees of the node to be deleted currently exist
if (node.left != null && node.right != null)
{
// Find the replacement node to delete the node
AVLTreeNode innext = node.right;
//Parent nodes of nodes to be replaced
AVLTreeNode innextParent=node;
// Find the leftmost child node under the right subtree
while (innext.left != null)
{
innextParent=innext;
innext = innext.left;
}
// Changing Relevant Data of Deleted Nodes
node.data = innext.data;
node.key = innext.key;
//Recursively delete nodes to replace them
remove(node.right,innext.key,node);
//Determine whether the deleted node is "unbalanced" and rotate the path from the current deleted node to the parent node of the corresponding replacement node.
rotate(node,null,innextParent);
}
// The following considerations are all the cases where the deletion node currently lacks a left subtree or a right subtree
else
{
// When the node to be deleted is not the root node
if (parent != null)
{
// When the left subtree is not empty
if (node.left != null && node.right == null)
{
// When the current node is its left subtree node
if (node == parent.left)
{
parent.left = node.left;
}
// When the current node is its right subtree node
else
{
parent.right = node.left;
}
if(node.left!=null)
{
//Because the deletion node lacks the left subtree or the right subtree. Therefore, it only needs to judge the unbalance of the parent node of the deleted node and adjust it accordingly.
rotate(parent,null,node.left);
}
}
// When the right subtree is not empty or is a leaf node
else
{
// When the current node is its left subtree node
if (node == parent.left)
{
parent.left = node.right;
}
// When the current node is its right subtree node
else
{
parent.right = node.right;
}
if(node.right!=null)
{
//Because the deletion node lacks the left subtree or the right subtree. Therefore, it only needs to judge the unbalance of the parent node of the deleted node and adjust it accordingly.
rotate(parent,null,node.right);
}
}
}
// When the currently deleted node is the root node
else
{
if (node.left != null)
root = node.left;
else
root = node.right;
}
}
// Returns the value of the node it deletes
return result;
}
}
return null;
}The complete sample code is as follows:
Related codes:
package all_in_tree;
/**
* This class is used to demonstrate the operation of balanced binary tree
* @author Apprentice
*
*/
public class AVLTree
{
//The Root Node of the Equilibrium Binary Tree
private AVLTreeNode root;
/**
* Follow-up traversal of the balanced binary tree (the results of post-traversal are sorted in order) is performed to verify the results of its tests.
*/
public static void inTravel(AVLTreeNode root)
{
if(root!=null)
{
inTravel(root.left);
System.out.print(root.key+"-"+root.data+"\t");
inTravel(root.right);
}
}
/**
* To obtain the balanced binary tree
* @return The root node pointer of the balanced binary tree
*/
public AVLTreeNode getTree()
{
return this.root;
}
/**
* Used to get the depth of a tree with root as its root node
* @param root Root node pointer to the depth of the tree to be retrieved
* @return The depth of a tree with root as its root node
*/
private int getDepth(AVLTreeNode root)
{
if(root==null)
return 0;
return Math.max(getDepth(root.left),getDepth(root.right))+1;
}
/**
* Used to judge the balance of the binary tree with root node, true is balanced, false is not balanced.
* @param root The root node pointer of the subtree to determine its equilibrium factor
* @return Equilibrium of Equilibrium Binary Tree with root as root Node
*/
private boolean isBalance(AVLTreeNode root)
{
return Math.abs(getDepth(root.left)-getDepth(root.right))<=1;
}
/**
* Equilibrium Factor of Binary Tree with root as root Node
* @param root A pointer to the root node of a subtree for finding its equilibrium factor
* @return Equilibrium factor
*/
private int getBalance(AVLTreeNode root)
{
return getDepth(root.left)-getDepth(root.right);
}
/**
* Used to balance the search operation in the binary tree, and return the relevant data of the corresponding node, when not found, return null
* @param key Keyword for the node to be looked up
* @return Get the relevant data for the node to be looked up
*/
public Object search(Comparable key)
{
if(key==null)
return null;
return getSearchResult(root,key);
}
/**
* Used to assist the balanced binary tree lookup operation, and return the data of the relevant nodes, when not found, return null
* @param root The root node of the binary search tree for lookup
* @param key Keyword for the node to be looked up
* @return Get the relevant data for the node to be looked up
*/
private Object getSearchResult(AVLTreeNode root,Comparable key)
{
if(root==null)
return null;
int compare=key.compareTo(root.key);
if(compare==0)
return root.data;
else if(compare==1)
return getSearchResult(root.right,key);
else
return getSearchResult(root.left,key);
}
/**
* Right-handed operation with the pointer of the incoming node as the binary tree of the root node
* @param node The root node of a right-handed binary tree
* @return Pointer of the root node of the rotated binary tree
*/
private AVLTreeNode rightRotate(AVLTreeNode node)
{
//Used to record rotated results
AVLTreeNode result=node.left;
node.left=result.right;
result.right=node;
return result;
}
/**
* The binary tree with the pointer of the incoming node as the root node performs the left-handed operation
* @param node The root node of a left-handed binary tree
* @return Pointer of the root node of the rotated binary tree
*/
private AVLTreeNode leftRotate(AVLTreeNode node)
{
//Used to record rotated results
AVLTreeNode result=node.right;
node.right=result.left;
result.left=node;
return result;
}
/**
* Used to insert new nodes into a binary tree
* @param key Key words of new nodes in binary tree
* @param data Data of New Nodes in Binary Tree
* @return The result of inserting a new node returns true if it succeeds in inserting a new node, false if it does not, and false if the new node exists in the tree.
*/
public boolean insert(Comparable key,Object data)
{
if(key==null)
return false;
else if(root!=null)
{
return insertAVLTreeNode(root,null,key,data);
}
else
{
root=new AVLTreeNode(key,data);
return true;
}
}
/**
* Assist in inserting new nodes into the binary tree
* @param node Nodes of binary trees to be compared
* @param parent The parent node of the node of the binary tree to be compared
* @param key Key Value of New Node
* @param data Data of new nodes
* @return Additional results
*/
private boolean insertAVLTreeNode(AVLTreeNode node,AVLTreeNode parent,Comparable key,Object data)
{
//When the current comparison node is not empty, the comparison operation is performed
if(node!=null)
{
int compare=key.compareTo(node.key);
if(compare==0)
return false;
else if(compare>0)
return insertAVLTreeNode(node.right,node,key,data);
else
return insertAVLTreeNode(node.left,node,key,data);
}
//When the current node is empty, insert the node from its parent node. At the same time, the rotation judgement and corresponding operation are carried out.
else
{
Comparable parentKey=parent.key;
AVLTreeNode newNode=new AVLTreeNode(key,data);
int comparable=parentKey.compareTo(key);
//Insert new nodes
if(comparable>0)
parent.left=newNode;
else
parent.right=newNode;
//The nodes after insertion are judged to see if they need to rotate. When necessary, the nodes of the balanced binary tree are rotated and adjusted.
rotate(root,null,newNode);
return true;
}
}
/**
* It is used to assist the judgement of whether the newly inserted node rotates or not and to make corresponding operations.
* @param root Current node lookup
* @param parent Parent Node of Current Find Node
* @param node The termination node of the path for rotation
*/
private void rotate(AVLTreeNode root,AVLTreeNode parent,AVLTreeNode node)
{
//From this, we can get the direction of the current lookup node.
int compare=root.key.compareTo(node.key);
//When the new node is found, the equilibrium factor of each node on its path is not "unbalanced", and it returns directly without operation.
if(compare==0)
{
return;
}
//When balanced and the current node's keyword value is less than the new node's keyword value, look to the right.
else if(compare<0&&isBalance(root))
{
//When the root node on its path is balanced, look to the right.
rotate(root.right,root,node);
}
//When balanced and the current node's keyword value is greater than the new node's keyword value, look to the left.
else if(compare>0&&isBalance(root))
{
//When the root node of the subtree on its path is balanced, look to the left
rotate(root.left,root,node);
}
//When unbalanced, rotate it
else
{
//When its parent node is null, there is no need to rotate it, because the number of nodes in the tree does not exceed three, so there must be no imbalance.
if(parent!=null)
{
//When it is unbalanced, rotate it.
//Used to determine whether it is unbalanced from the left or right of its parent node
boolean isLeft=parent.left.key.compareTo(root.key)==0?true:false;
//Equilibrium Factor for Obtaining the Unbalanced Node
int balance=getBalance(root);
//When it is greater than 0, either LL-type rotation or LR-type rotation is performed.
if(balance>0)
{
//It is used to obtain the balance factor of its child node and rotate it accordingly according to its balance factor.
int childBalance=getBalance(root.left);
//Left-rotate the subtree whose corresponding child node is the root node
if(childBalance<0)
{
root.left=leftRotate(root.left);
}
//Right-handed operations on trees with unbalanced root nodes as subtrees
AVLTreeNode rotateNode=rightRotate(root);
if(isLeft)
parent.left=rotateNode;
else
parent.right=rotateNode;
}
//When less than 0, either RR-type rotation or RL-type rotation is performed.
else
{
//It is used to obtain the balance factor of its child node and rotate it accordingly according to its balance factor.
int childBalance=getBalance(root.right);
//Right-handed the tree whose corresponding child node is the root
if(childBalance>0)
{
root.right=rightRotate(root.right);
}
//Left-handed operations on trees with unbalanced root nodes as subtrees
AVLTreeNode rotateNode=leftRotate(root);
if(isLeft)
parent.left=rotateNode;
else
parent.right=rotateNode;
}
}
}
}
/**
* Used for deletion operations
* @param key Keyword values of nodes to be deleted
* @return Returns the data value of the deleted node and null when there is no associated deleted node
*/
public Object delete(Comparable key)
{
if(key==null)
return null;
else
return remove(root,key,null);
}
/**
* A method for assisting with deletion operations
* @param node Current comparison node
* @param parent Parent Node of Current Compare Node
* @param key Keyword values of nodes that need to be deleted
* @return Returns the keyword of the deleted node
*/
public Object remove(AVLTreeNode node,Comparable key,AVLTreeNode parent)
{
if (node != null)
{
int compare = key.compareTo(node.key);
// Delete from the left subtree
if (compare < 0)
{
return remove(node.left, key, node);
}
// Delete from the right subtree
else if (compare > 0)
{
return remove(node.right, key, node);
}
// The current node is the node to be deleted
else
{
// Data of the node currently to be deleted
Object result = node.data;
// The left and right subtrees of the node to be deleted currently exist
if (node.left != null && node.right != null)
{
// Find the replacement node to delete the node
AVLTreeNode innext = node.right;
//Parent nodes of nodes to be replaced
AVLTreeNode innextParent=node;
// Find the leftmost child node under the right subtree
while (innext.left != null)
{
innextParent=innext;
innext = innext.left;
}
// Changing Relevant Data of Deleted Nodes
node.data = innext.data;
node.key = innext.key;
//Recursively delete nodes to replace them
remove(node.right,innext.key,node);
//Determine whether the deleted node is "unbalanced" and rotate the path from the current deleted node to the parent node of the corresponding replacement node.
rotate(node,null,innextParent);
}
// The following considerations are all the cases where the deletion node currently lacks a left subtree or a right subtree
else
{
// When the node to be deleted is not the root node
if (parent != null)
{
// When the left subtree is not empty
if (node.left != null && node.right == null)
{
// When the current node is its left subtree node
if (node == parent.left)
{
parent.left = node.left;
}
// When the current node is its right subtree node
else
{
parent.right = node.left;
}
if(node.left!=null)
{
//Because the deletion node lacks the left subtree or the right subtree. Therefore, it only needs to judge the unbalance of the parent node of the deleted node and adjust it accordingly.
rotate(parent,null,node.left);
}
}
// When the right subtree is not empty or is a leaf node
else
{
// When the current node is its left subtree node
if (node == parent.left)
{
parent.left = node.right;
}
// When the current node is its right subtree node
else
{
parent.right = node.right;
}
if(node.right!=null)
{
//Because the deletion node lacks the left subtree or the right subtree. Therefore, it only needs to judge the unbalance of the parent node of the deleted node and adjust it accordingly.
rotate(parent,null,node.right);
}
}
}
// When the currently deleted node is the root node
else
{
if (node.left != null)
root = node.left;
else
root = node.right;
}
}
// Returns the value of the node it deletes
return result;
}
}
return null;
}
/**
* test case
* @param args Initialization parameter array
*/
public static void main(String[] args)
{
AVLTree tree=new AVLTree();
tree.insert(5,"A");
tree.insert(2,"B");
tree.insert(6,"D");
tree.insert(1,"E");
tree.insert(3,"C");
tree.insert(4,"F");
AVLTree.inTravel(tree.getTree());
System.out.println();
System.out.println(tree.delete(1));
AVLTree.inTravel(tree.getTree());
System.out.println();
System.out.println(tree.search(5));
}
}
//The results are as follows:
1-E 2-B 3-C 4-F 5-A 6-D
E
2-B 3-C 4-F 5-A 6-D
A
The diagrams used in the test cases are as follows: