task

solution

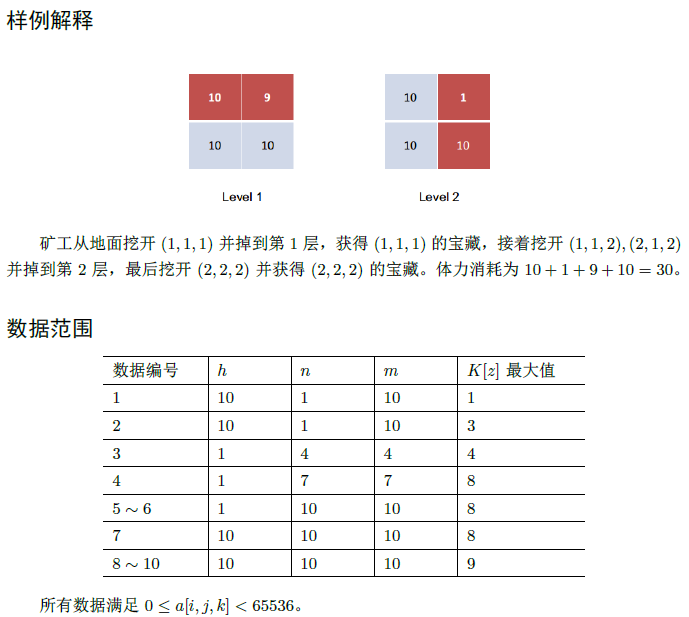
Considering the two-dimensional case,
It can be found that the smallest spanning tree for a given point is called a Steiner tree.
Notice that the number of points is very small.
We can use state compression Dp to solve the problem.
Let f[i][j][s] denote that (i,j) i s the root and the connected state i s the minimum cost of S.
Obviously, yes.

Be aware,
When transferring, because s'< s, f[][][s'] is already calculated, so it can be transferred directly.
However, we find that there is a clear possibility of circular updates when using transfer 2.
Ordinary recursion is obviously not applicable;
However, because it satisfies the triangular inequality relationship, it can be transformed into SPFA to transfer.

Generally speaking, we first transfer all the points that can be updated into the queue, and then unify SPFA.
The two-dimensional situation is solved.

Next, let's consider the three-dimensional situation.
We need a recursive method between layers.
We add a special treasure to each layer. Only when we pay the price of the front layer can we get the treasure.
Then we can deal with the three-dimensional situation.

Code

#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<math.h>
#define ll long long
using namespace std;
const char* fin="treasure.in";
const char* fout="treasure.out";
const ll inf=0x7fffffff;
const ll maxn=11,Maxn=107,maxm=Maxn*80,maxk=1<<10;
const ll w[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
ll N,n,m,i,j,k,x,y,l;
ll a[maxn][maxn][maxn],b[maxn][maxn*maxn][2],c[maxn];
ll f[maxn][maxn][maxn][maxk];
ll trea[maxn][maxn][maxn];
ll head,tail,B[maxn*maxn*800][2];
bool bz[maxn][maxn];
void add_tail(ll x,ll y){
    B[++tail][0]=x;
    B[tail][1]=y;
    bz[x][y]=true;
}
void add(ll z,ll x,ll y,ll st,ll d){
    if (f[z][x][y][st]>d){
        f[z][x][y][st]=d;
        if (!bz[x][y]) add_tail(x,y);
    }
}
void spfa(ll sz,ll st){
    ll i,j,k;
    while (head++<tail){
        for (i=0;i<4;i++){  
            j=B[head][0]+w[i][0];
            k=B[head][1]+w[i][1];
            if (j>0 && j<=n && k>0 && k<=m) add(sz,j,k,st,f[sz][B[head][0]][B[head][1]][st]+a[sz][j][k]);
        }
        bz[B[head][0]][B[head][1]]=false;
    }
    head=tail=0;
}
int main(){
    freopen(fin,"r",stdin);
    freopen(fout,"w",stdout);
    scanf("%lld%lld%lld",&N,&n,&m);
    for (i=1;i<=N;i++) for (j=1;j<=n;j++) for (k=1;k<=m;k++) scanf("%lld",&a[i][j][k]);
    for (i=1;i<=N;i++){
        scanf("%lld",&c[i]);
        for (j=1;j<=c[i];j++){
            scanf("%lld%lld",&b[i][j][0],&b[i][j][1]);
            trea[i][b[i][j][0]][b[i][j][1]]=j;
        }
        if (i>1) c[i]++;
    }
    ll ans=inf;
    memset(f,127,sizeof(f));
    for (i=1;i<=N;i++){
        for (j=1;j<=n;j++)
            for (k=1;k<=m;k++)
                if (trea[i][j][k]) f[i][j][k][1<<(trea[i][j][k]-1)]=a[i][j][k];
                else f[i][j][k][0]=a[i][j][k];
        for (l=0;l<1<<c[i];l++){
            for (j=1;j<=n;j++)
                for (k=1;k<=m;k++){
                    for (ll L=l&(l-1);L;L=l&(L-1)){
                        if (f[i][j][k][L]<2000000000 && f[i][j][k][l-L]<2000000000)
                            f[i][j][k][l]=min(f[i][j][k][l],f[i][j][k][L]+f[i][j][k][l-L]-a[i][j][k]);
                    }
                    if (f[i][j][k][l]<2000000000) add_tail(j,k);
                }
            spfa(i,l);
            if (l==(1<<c[i])-1)
                for (j=1;j<=n;j++) for (k=1;k<=m;k++){
                    if (f[i][j][k][l]>2000000000) continue;
                    if (i==N) ans=min(ans,f[i][j][k][l]);
                    else if (trea[i+1][j][k])
                        f[i+1][j][k][(1<<(c[i+1]-1))|(1<<(trea[i+1][j][k]-1))]=a[i+1][j][k]+f[i][j][k][l];
                    else f[i+1][j][k][(1<<(c[i+1]-1))]=a[i+1][j][k]+f[i][j][k][l];
                }
        }
    }
    printf("%lld",ans);
    return 0;
}

Warning

1. When moving to the next level, in fact, I mistakenly believed that the cost of the front layer must be included, so I could not deal with some situations.
2. When SPFA is used in the same layer, it is not necessary to avoid encountering black spots.
3. Tips.
Enumerate the true subset of a binary number:

for (i=j;i;i=j&(i-1))

The general idea is to delete the last one every time.
Then wait until it turns to 1000. After the form of 1000, it will be shortened by one and enumerated again.