subject

Given two linked lists, determine whether they intersect

Overview:

1. Find the entry points node 1 and node2 of the two linked lists
2. If one of the nodes 1 and 2 is empty and the other is not, the two linked lists cannot intersect.
3. If both node1 and node2 are empty, indicating that the two linked lists are not linked, then the first intersection point can be obtained by judging the two linked lists.
4. If node1 and node2 are not empty, it means that both lists have rings and need to be discussed separately.

• The same entry point and the first intersection point
• Nodes with the same entry point and not the first intersection
• The entry points are different. If one entry point encounters another entry point of the list in the process of returning to itself, it intersects, otherwise it does not want to intersect. In the case of intersection, any entry point can be returned as the first intersection point.

1. Two linked lists do not have rings, so we can judge the intersection (the intersection of linked lists refers to the same address, not the same object in the node).
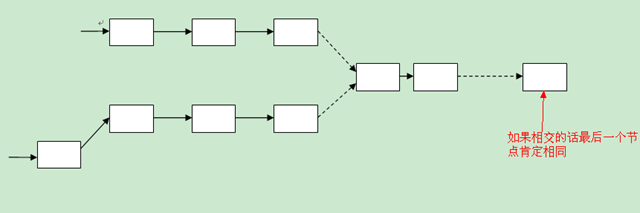
When two acyclic lists intersect, the last node of the two lists must be equal.

/**
 * Now there are two acyclic single-linked lists, if the length of the two lists is m and n, respectively.
 * Please design an algorithm with O(n + m) time complexity and O(1) extra space complexity to determine whether the two linked lists intersect.
 * Given the header nodes headA and headB of two linked lists, return a bool value.
 * Represents whether the two linked lists intersect. Make sure that the length of the two lists is less than or equal to 500.
 *
 * Note: List intersection refers to the same address, not the same value in the list.
 */

private class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
public boolean chkIntersect(ListNode headA, ListNode headB) {
    // write code here
    while (headA.next != null) {
        headA = headA.next;
    }
    while (headB.next != null) {
        headB = headB.next;
    }
    return headA == headB;
}

If you need to return the first intersection of two linked lists, you can do this:

• First traverse the two lists to get the length of the two lists
• Then move the long list to the same length as the short list.
• Then move the two lists together until the same node is the first intersecting node.

2. The intersection of two linked lists

* If linked lists are looped and intersected, then both linked lists are looped

Specific steps:

1. First, find the entry point of two linked lists. If the two entry points are the same point, the two linked lists intersect.

2. If you look for the first intersection point of two linked lists, you may see the following picture
Namely, if two linked lists intersect before entering the ring, the part before entering the ring can be regarded as finding the first intersection point of two acyclic single linked lists.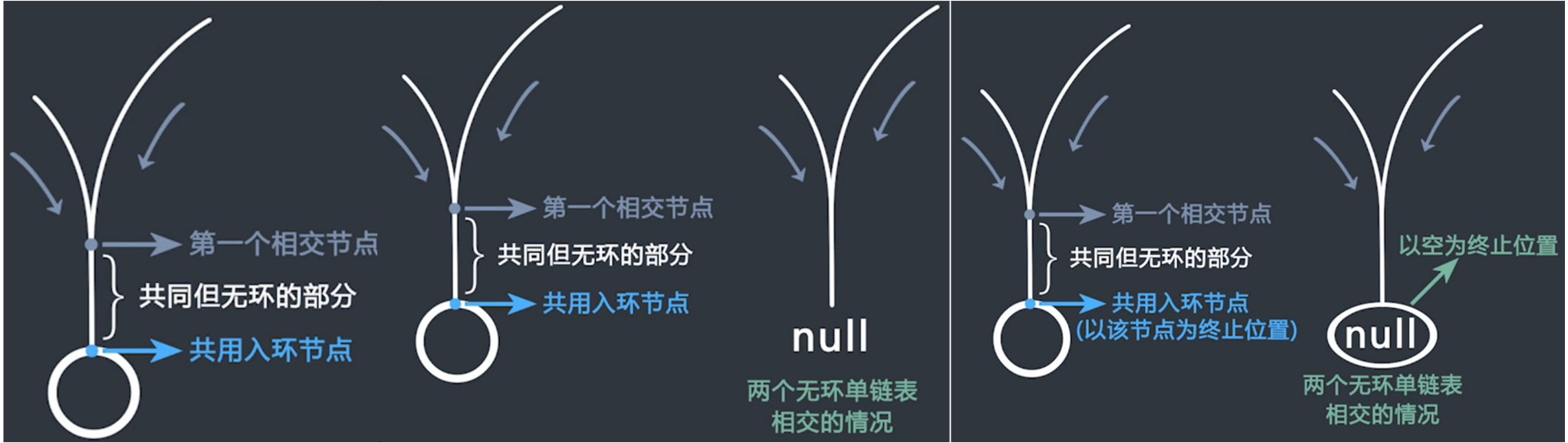


The following is the case where the entry points of two linked lists are different:

1. Case 1: In the process of node1 moving forward to node1, there is no entry point of list 2, and it returns to empty directly.
2. Case 2: In the process of node1 moving forward to node1, we encounter node2, the entry point of chain 2. At this time, we can but will node1 (the first intersection point closer to chain table 1) or node2 (the first intersection point closer to chain table 2).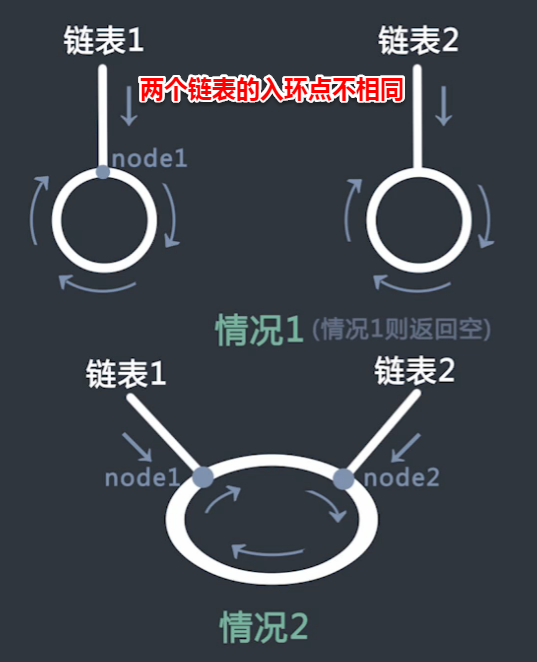


3. When one linked list has a link and the other has no link, the two linked lists must not intersect.
4. Judging whether two linked lists intersect

/**
 * Given the header nodes head1 and head2 of two single linked lists, how to judge whether the two linked lists intersect? Return true if you intersect, false if you don't want to intersect.
 * Given the header nodes head1 and Head2 of two linked lists (note that the other two parameters, adjust0 and adjust1, are used to adjust the data, independent of the solution of this problem).
 * Please return a bool value to indicate whether they intersect.
 */

private class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
public boolean chkInter(ListNode head1, ListNode head2, int adjust0, int adjust1) {
    // write code here
    // First, determine whether two linked lists have rings or not.
    // A ring and an acyclic must not intersect
    // Two acyclic, judging whether the two endpoints are equal or not, they intersect if they want to wait, otherwise they do not intersect.
    // Both have rings. If the entry points are the same, they intersect, and if they are not equal, they traverse one of the rings to determine whether another entry point can be encountered in the process of traversal, and if not, they are equal, otherwise they are not equal.
    ListNode node1 = getNode(head1);
    ListNode node2 = getNode(head2);
    if (node1 == null && node2 != null || node1 != null && node2 == null) {//A ring and an acyclic
        return false;
    } else if (node1 == null && node2 == null) {//Neither of them is ringless.
        while (node1.next != null) {
            node1 = node1.next;
        }
        while (node2.next != null) {
            node2 = node2.next;
        }
        return node1 == node2;
    } else {//Both have rings
        if (node1 == node2) {
            return true;
        }
        ListNode flag = node1.next;
        while (node1 != flag) {
            if (flag == node2) {
                return true;
            }
            flag = flag.next;
        }
    }
    return false;
}

//Find the entry point of the list and return to the entry point if it exists, otherwise null will occur.
private static ListNode getNode(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;
    while (fast.next.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) {//Fast and slow pointers meet for the first time in the ring
            break;
        }
    }
    if (fast != slow) {
        return null;
    }
    fast = head;
    while (fast != slow) {
        fast = fast.next;
        slow = slow.next;
    }
    return fast;
}