Quick sorting and merging of JS sorting algorithm
Quick sort
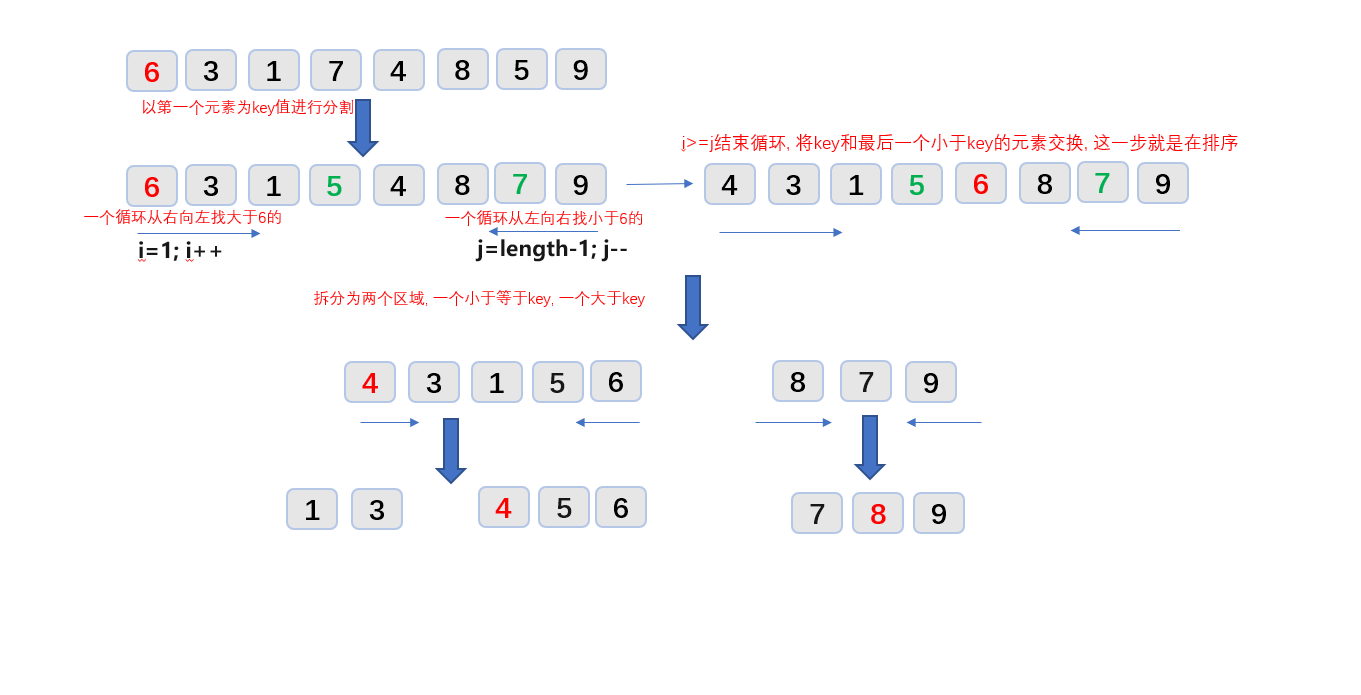
Principle: select a key (generally the first element) and divide the array into two regions. All the regions on the left are less than or equal to the key, and all the regions on the right are greater than the key. Then divide each region into two regions by this method. The whole process can be realized recursively, so as to realize the whole data order
- Time complexity: O(n*log(n))
- Worst time complexity: O(n^2)
- Worst case: the original array is in ascending (descending) order and needs to be sorted in descending (ascending) order
- Unstable sorting
- Property: the array is divided into blocks, and the left area is smaller than the right (ascending)
- Unstable reason: element exchange is a direct exchange across elements, and adjacent identical elements may exchange positions
- Performance: the best quick sorting method
Example process:
function quickSort(ary) {
let n = ary.length;
function sort(ary, start, end) {
if(end <= start) return;
let i = start,
j = end,
key = ary[start]; // Set the first element to key
while(true) {
// Find the element position greater than key from left to right (the cycle stop greater than key, i is the element position)
while(ary[++i] < key) {
// End of loop exit
if(i === end) break;
}
// Find the element position smaller than key from right to left
while(ary[--j] > key) {
// Reach head exit loop
if(j === start) break;
}
// If i and j intersect, exit the loop directly
if(i>=j) break;
// Exchange left and right elements
let temp = ary[i];
ary[i] = ary[j];
ary[j] = temp;
}
// Exchange the key and the last element less than the key value (that is, arr[j])
let temp = ary[start];
ary[start] = ary[j];
ary[j] = temp;
sort(ary, start, j);
sort(ary, j+1, end);
}
sort(ary, 0, n);
return ary;
}Effect demonstration:

Merge sort
Principle: first, divide the array into two small arrays, then sort and merge them
- Time complexity: O(n*log(n))
- Stable sorting algorithm
- Stable reason: sorting is the interchange between two element values, and the position of adjacent identical elements will not be changed
- Performance: the speed is only second and fast (if recursive method is used, there may be insufficient memory when processing large data), which is more stable than fast scheduling, and the time complexity is O(n*long(n));
- Features: the array will continue to bisect, and then sort and merge. First, the cells are ordered, then the large interval, and the interval interval is equal
- Optimization: TimeSort sorting
Example process: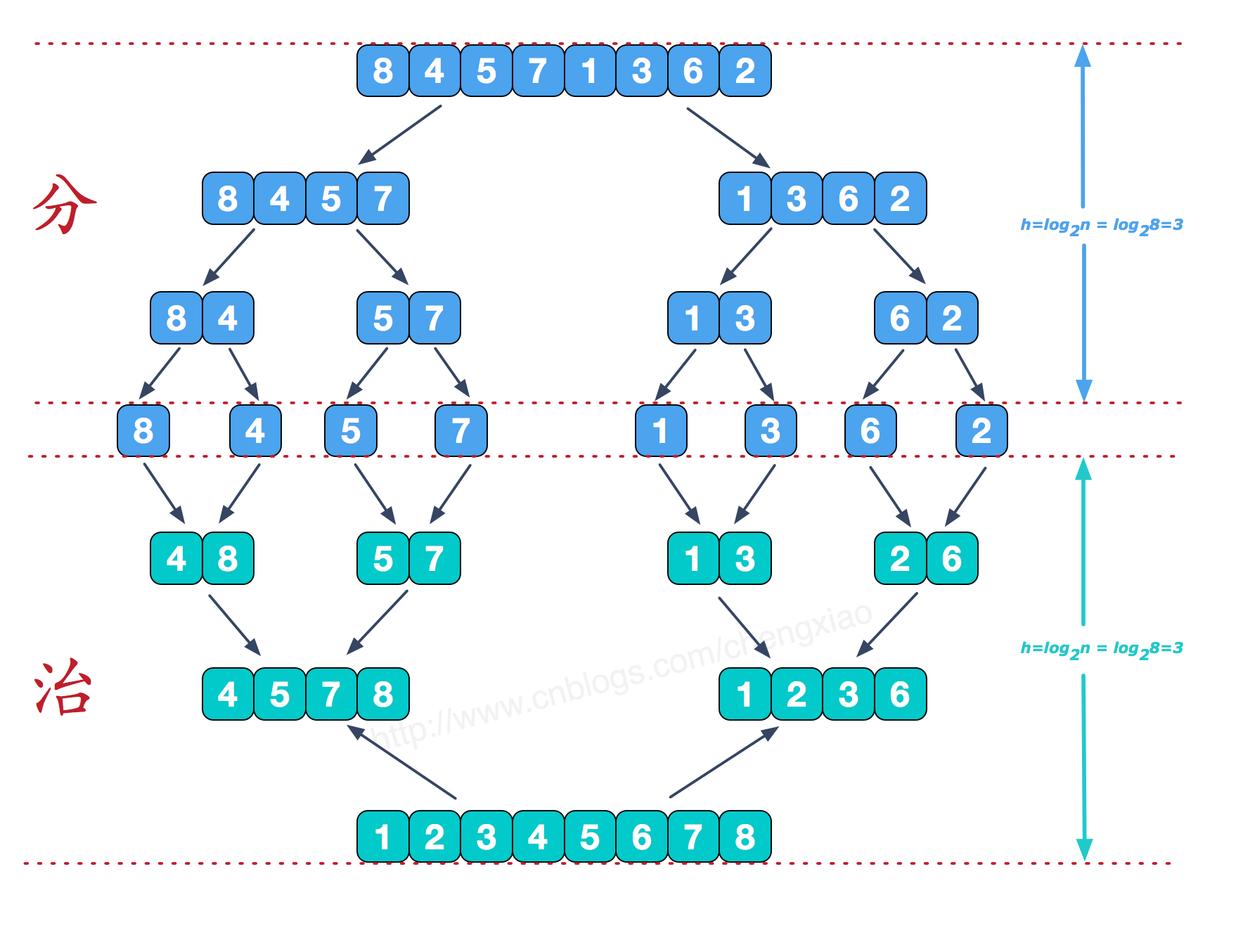
function mergeSort(items) {
if (items.length == 1) {
return items;
}
//Divide the array into left and right arrays
var middle = Math.floor(items.length / 2),
left = items.slice(0, middle),
right = items.slice(middle);
function merge(left, right) {
var result = [];
// Sort by this loop
while (left.length > 0 && right.length > 0) {
if (left[0] < right[0]) {
/*shift()Method is used to remove the first element of an array and return the value of the first element.*/
result.push(left.shift());
} else {
result.push(right.shift());
}
}
//Merge two arrays
return result.concat(left).concat(right);
}
// Recursive call
return merge(mergeSort(left), mergeSort(right));
}Example of effect

gif source: Sorting algorithm - scatter visualization