Tree is a non-linear data structure, which stores data in a hierarchical way. Trees are used to store hierarchical data, such as files in file systems; trees are also used to store ordered lists.
Advantages: Finding on a binary tree is very fast (not on a linked list), adding or deleting elements for a binary tree is also very fast (but not for adding or deleting arrays).
Definition of 1 Tree
The tree consists of a set of nodes connected by edges. Each box is a node, and the line connecting the box is called the edge.
The top node of a tree is called the root node. If multiple nodes are connected below a node, the node is called the parent node, and the node below it is called the child node. A node can have 0, 1 or more sub-nodes. Nodes without any sub-nodes are called leaf nodes.

Binary tree is a special kind of tree, whose number of sub-nodes is not more than two.
Along a specific set of edges, you can walk from one node to another that is not directly connected to it. The set of edges from one node to another is called paths, which are represented by dotted lines in the graph. Accessing all nodes in the tree in a particular order is called tree traversal.
Trees can be divided into several levels, the root node is the 0th level, its sub-nodes are the 1st level, and the sub-nodes of sub-nodes are the 2nd level, and so on. Nodes at any level of the tree can be regarded as the root of the subtree, which contains the child nodes of the root node, the child nodes of the child node and so on. We define the number of layers of a tree as the depth of the tree.
Each node has a value associated with it, sometimes referred to as a key.
2 Binary Tree and Binary Search Tree
The two children of a parent node are called left node and right node respectively. Binary lookup tree is a special kind of binary tree. Relatively small values are stored in the left node and larger values are stored in the right node.
1 Implementing Binary Search Tree
//Save data, save links to other nodes
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
//Display the data stored in the node.
function show() {
return this.data;
}
Create a class to represent a binary search tree (BST).
Class contains only one data member: a Node object representing the root node of a binary lookup tree. The constructor of this class initializes the root node to null to create an empty node.
BST must first have an insert() method to add new nodes to the tree.
First, create a Node object and pass the data into the object to save.
Second, check whether BST has a root node, if not, then this is a new tree, the node is the root node, this method is completed; otherwise, go to the next step.
If the node to be inserted is not the root node, then you need to prepare to traverse the BST to find the appropriate location for insertion. This process is similar to traversing linked lists. Store the current node with a variable and traverse the BST layer by layer. After entering BST, the next step is to decide where to place the nodes. When you find the correct insertion point, you jump out of the loop. The algorithm for finding the correct insertion point is as follows.
(1) Set the root node as the current node.
(2) If the data saved by the inserting node is less than the current node, the new current node is the left node of the original node; otherwise, step 4 is executed.
(3) If the left node of the current node is null, insert the new node into this location and exit the loop; otherwise, continue to execute the next cycle.
(4) Let the new current node be the right node of the original node.
(5) If the right node of the current node is null, insert the new node into this location and exit the loop; otherwise, continue the next cycle.
// Binary Search Tree BST
// There is a node attribute, and there are other ways to define a binary lookup tree BST class
function BST(){
// The root node is initialized to be empty
this.root = null;
// Method
// insert
this.insert = insert;
// Sequential traversal
this.inorder = inorder;
// Preorder traversal
this.preorder = preorder;
// Post order traversal
this.postorder = postorder;
}
//Insert insert insert method
function insert(data){
// Create a node to save data
var node = new Node(data,null,null);
// Next insert node into the tree
// If the tree is empty, set the node to the root node
if(!this.root){
this.root = node;
}else{ //Trees are not empty.
// Determine whether to insert it on the left or right side of the parent node
// So first save the parent node
var current = this.root;
var parent;
// If the key value of the node to be inserted is less than that of the parent node, it is interpolated to the left of the parent node.
// The premise is that the left side of the parent node is empty, otherwise the parent node should be moved down one layer.
// Then make a judgement.
//while(true) denotes an infinite loop
while(true){
// data is less than the key value of the parent node
parent = current;
if(data < parent.data){
// Move the parent down to the left (insert to the left)
//Note: The parent node keeps moving down!!!
current = current.left;
// If the node is empty, insert it directly
if(current == null){
parent.left = node;
break;
}
}else{ // Move the parent node down to the right (insert right)
current = current.right;
if(!current){
parent.right = node;
break;
}
}
}
}
}
Write a binary tree:
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
print("Inorder traversal: ");
inOrder(nums.root);
Output is: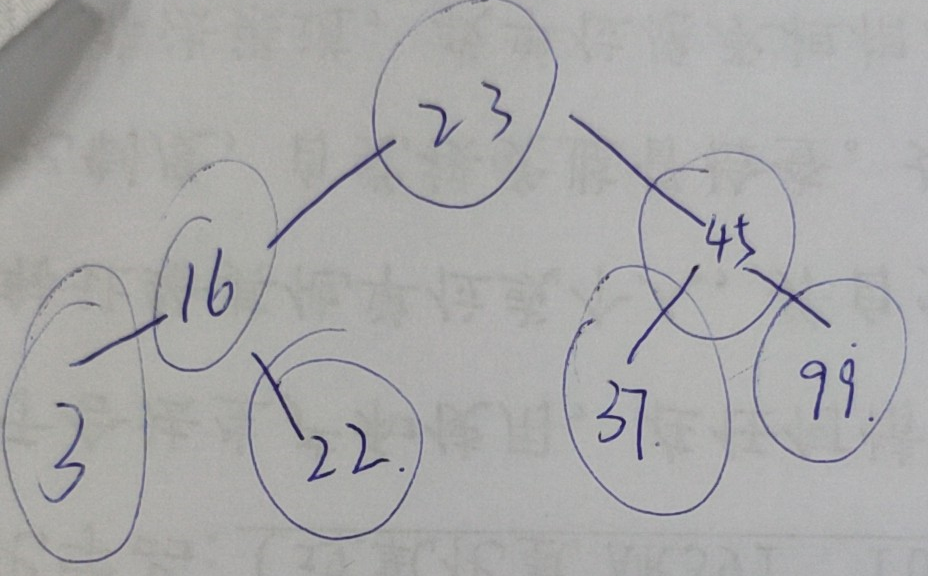
2-traversal binary search tree
(1) In order traversal, recursive method is the easiest way to achieve. This method needs to access all the nodes in the tree in ascending order, first the left subtree, then the root node, and finally the right subtree.
function inOrder(node) {
if (!(node == null)) {
inOrder(node.left);
putstr(node.show() + " ");
inOrder(node.right);
}
}
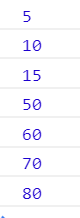
The results showed that: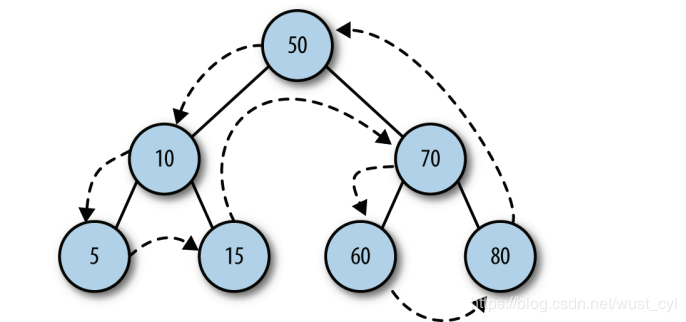
(2) The definition of sequential traversal is as follows: sequential traversal first accesses the root node, then accesses the left subtree and the right subtree in the same way.
function preOrder(node) {
if (!(node == null)) {
putstr(node.show() + " ");
preOrder(node.left);
preOrder(node.right);
}
}
Results show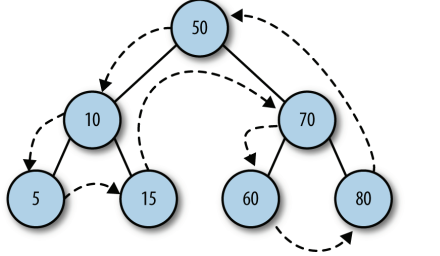
Output 50, 10, 5, 15, 70, 60, 80
Note: The only difference between the inOrder() and preOrder() methods is the order of the code show() functions in the if statement. In the inOrder() method, the show() function is sandwiched between two recursive calls; in the preOrder() method, the show() function precedes two recursive calls.
(3) Post-order traversal: Post-order traversal first accesses leaf nodes, from left subtree to right subtree, and then to root node.
function postOrder(node) {
if (!(node == null)) {
postOrder(node.left);
postOrder(node.right);
putstr(node.show() + " ");
}
}
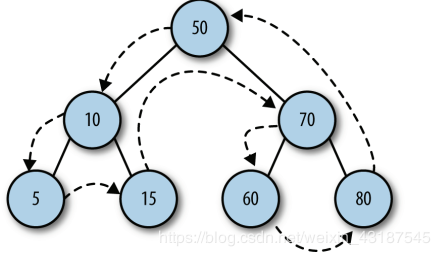
Output 5, 15, 10, 60, 80, 70, 50
3. Search on the binary search tree
1 Find the minimum and maximum
The getMin() method finds the minimum value on BST, because the smaller value is always on the left child node, and the smallest value is always on the BST. It only needs to traverse the left subtree until the last node is found. The method is defined as follows:
function getMin() {
var current = this.root;
//Walk one by one along the left subtree of BST until you reach the leftmost node of BST
while (!(current.left == null)) {
current = current.left;
}
return current.data;
}
The getMax() method is defined as follows:
function getMax() {
var current = this.root;
while (!(current.right == null)) {
current = current.right;
}
return current.data;
}
2 Find the given value
Finding a given value on BST requires comparing the value with the value on the current node. By comparison, we can determine whether to traverse left or right if the given value is not in the current node.
function find(data) {
var current = this.root;
while (current != null) {
if (current.data == data) {
return current;
}
else if (data < current.data) {
current = current.left;
}
else {
current = current.right;
}
}
return null;
}
4 Delete nodes from binary search tree
The deletion of binary tree nodes can also be divided into several cases:
The deleted node is a leaf node.
The deleted node has only one child node (subtree);
The deleted node has two child nodes (subtrees)
(1) The deleted node is a leaf node
Idea: Set the reference value of the parent node pointing to the child node of the leaf node to be empty
(2) The deleted node has only one subtree
Idea: Change the reference of the parent node to the node to the child node of the node.
(3) Deleting a node has two subtrees
Thought: There are two ways to deal with this situation:
Find the node A with the largest value from the left subtree of the node to be deleted, replace the node to be deleted, and delete node A;
Find the smallest node A from the right subtree of the node to be deleted, replace the node to be deleted, and delete node A.
---> Choose the second one and need a method to find the minimum value on the subtree.
// Getting the Minimum Binary Tree under a given Node
BST.prototype.getSmallest = function(node) {
if(node.left == null) {
return node;
} else {
return getSmallest(node.left);
}
};
// Delete the corresponding nodes of the binary tree under a given node according to the given node
BST.prototype.removeNode = function(node, data) {
if(node == null) {
return null;
}
if(data == node.data) {
// No child nodes (subtrees)
if(node.left == null && node.right == null) {
return null;
}
// Only right child nodes (subtrees)
else if(node.left == null ) {
return node.right;
}
// Only left child nodes (subtrees)
else if(node.right == null){
return node.left;
}
// There are two sub-nodes (sub-trees)
else {
var tempNode = this.getSmallest(node.right);
node.data = tempNode.data;
node.right = this.removeNode(node.right, tempNode.data);
return node;
}
} else if(data < node.data) {
node.left = this.removeNode(node.left, data);
return node;
} else {
node.right = this.removeNode(node.right, data);
return node;
}
}
5 count
Record the number of occurrences of data in a set of data sets
//Modify the definition of Node object to increase the number of members who record scores
function Node(data, left, right) {
this.data = data;
this.count = 1;
this.left = left;
this.right = right;
this.show = show;
}
// As the number of times increases, we need a new method to update the nodes in BST.
function update(data) {
var grade = this.find(data);
grade.count++;
return grade;
}
//Random Achievement
function genArray(length) {
var arr = [];
for (var i = 0; i < length; ++i) {
arr[i] = Math.floor(Math.random() * 101);
}
return arr;
}
//Display function
function prArray(arr) {
putstr(arr[0].toString() + ' ');
for (var i = 1; i < arr.length; ++i) {
putstr(arr[i].toString() + ' ');
if (i % 10 == 0) {
putstr("\n");
}
}
}