Reprinted from https://www.cnblogs.com/AlbertP/p/10847627.html
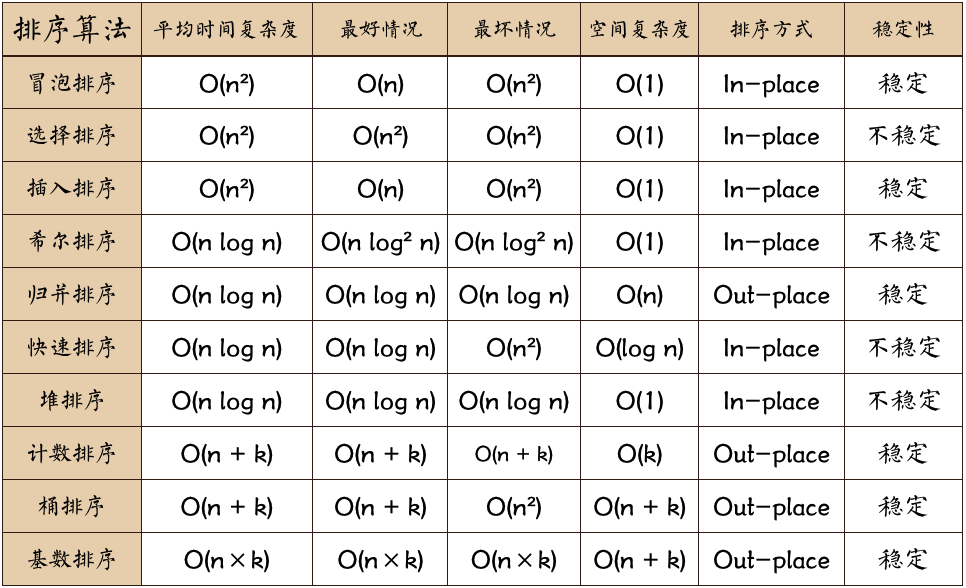
First, summarize the above figure

Bubble sorting

Idea: swap the largest number in the remaining array to the tail each time

function bubbleSort(arr) {
    var len = arr.length;
    for (var i = 0; i < len; i++) {
        for (var j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j+1]) {        //Pairwise comparison of adjacent elements
                var temp = arr[j+1];        //Element exchange
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

Select sort

One of the most stable sorting algorithms in terms of time complexity, because no matter what data goes in, it is O(n) ²) Time complexity... So when using it, the smaller the data size, the better. The only advantage may be that it does not occupy additional memory space.
Idea: pick the smallest number in the remaining array every time

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     //Find the smallest number
                minIndex = j;                 //Save the index of the smallest number
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

Insert sort

Idea: insert numbers into the previously ordered array every time

function insertionSort(arr) {
    var len = arr.length;
    var preIndex, current;
    for (var i = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while(preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex+1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex+1] = current;
    }
    return arr;
}

Shell Sort

Hill sort is a more efficient implementation of insertion sort. The difference between Hill sort and insertion sort is that it will give priority to comparing elements far away. The core of Hill sort is the setting of interval sequence. Interval sequence can be set in advance or defined dynamically. The algorithm for dynamically defining interval sequence is algorithm (4th Edition) It was proposed by Robert Sedgewick, co-author of. Here, I use this method.

function shellSort(arr) {
    var len = arr.length,
        temp,
        gap = 1;
    while(gap < len/3) {          //Dynamically define interval sequence
        gap =gap*3+1;
    }
    for (gap; gap > 0; gap = Math.floor(gap/3)) {
        for (var i = gap; i < len; i++) {
            temp = arr[i];
            for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) {
                arr[j+gap] = arr[j];
            }
            arr[j+gap] = temp;
        }
    }
    return arr;
}

Merge sort

Like the selective sort, the performance of merge sort is not affected by the input data, but it performs much better than the selective sort, because it is always the time complexity of O(n log n). The cost is the need for additional memory space.

function mergeSort(arr) {  //The top-down recursive method is adopted
    var len = arr.length;
    if(len < 2) {
        return arr;
    }
    var middle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right)
{
    var result = [];

    while (left.length && right.length) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }

    while (left.length)
        result.push(left.shift());

    while (right.length)
        result.push(right.shift());

    return result;
}

Quick row

In essence, quick sort should be regarded as a recursive divide and conquer method based on bubble sort.

function quickSort(arr, left, right) {
    var len = arr.length,
        partitionIndex,
        left = typeof left != 'number' ? 0 : left,
        right = typeof right != 'number' ? len - 1 : right;

    if (left < right) {
        partitionIndex = partition(arr, left, right);
        quickSort(arr, left, partitionIndex-1);
        quickSort(arr, partitionIndex+1, right);
    }
    return arr;
}

function partition(arr, left ,right) {     //Partition operation
    var pivot = left,                      //Set reference value (pivot)
        index = pivot + 1;
    for (var i = index; i <= right; i++) {
        if (arr[i] < arr[pivot]) {
            swap(arr, i, index);
            index++;
        }        
    }
    swap(arr, pivot, index - 1);
    return index-1;
}

function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

Heap sort

Heap sorting can be said to be a selective sorting using the concept of heap. It is divided into two methods:
Large top heap: the value of each node is greater than or equal to the value of its child nodes. It is used for ascending arrangement in heap sorting algorithm
Small top heap: the value of each node is less than or equal to the value of its child nodes. In the heap sorting algorithm, it is used to sort var len in descending order. / / because multiple functions declared need data length, set len as a global variable

function buildMaxHeap(arr) {   //Build large top reactor
    len = arr.length;
    for (var i = Math.floor(len/2); i >= 0; i--) {
        heapify(arr, i);
    }
}

function heapify(arr, i) {     //Heap adjustment
    var left = 2 * i + 1,
        right = 2 * i + 2,
        largest = i;

    if (left < len && arr[left] > arr[largest]) {
        largest = left;
    }

    if (right < len && arr[right] > arr[largest]) {
        largest = right;
    }

    if (largest != i) {
        swap(arr, i, largest);
        heapify(arr, largest);
    }
}

function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

function heapSort(arr) {
    buildMaxHeap(arr);

    for (var i = arr.length-1; i > 0; i--) {
        swap(arr, 0, i);
        len--;
        heapify(arr, 0);
    }
    return arr;
}

The rest are not commonly used in my opinion, so I will not summarize the original links at the top one by one