What does Joseph's problem describe?
Joseph's problem: there are N people in a circle, and each person has a number. The number is determined by the order of entering the circle. The first person entering the circle is numbered 1, and the last one is N. The number starts from the K (1 < = k < = N), and the person counting to m (1 < = m < = N) will leave the circle, and then the next person continues to count from 1 until everyone leaves the circle, so as to find the number of the circle in turn.
How to store data
Facing a problem, we first need to think about what kind of data structure to use to save data. Joseph problem describes the problem of circular counting out of circles. The counting is always carried out in the same direction, so it can be stored using a one-way ring linked list.
Whenever a person enters the circle, a new node is created, and the nodes are connected end to end. The code is as follows:
//node
class Node {
//Node serial number
private Integer no;
//A reference to the next node
private Node next;
public Node(Integer no) {
this.no = no;
}
@Override
public String toString() {
return "Node{" +
"no=" + no +
",next=" + (next == null ? "" : next.no) +
'}';
}
}
//Unidirectional ring linked list
class SingleCycleLinkedList {
//Header reference
private Node head;
//Tail reference
private Node tail;
//Linked list length
private int size;
/**
* Initializes the circular linked list with increasing sequence number of the specified length
*
* @param size
*/
public SingleCycleLinkedList(int size) {
for (int i = 1; i <= size; i++) {
add(new Node(i));
}
this.size = size;
}
/**
* Insert circular linked list
*
* @param node
*/
public void add(Node node) {
if (node == null) {
return;
}
//If the linked list is empty, directly point the head and tail references to the new node
if (size == 0) {
head = node;
tail = node;
size++;
return;
}
//The linked list is not empty. Put the new node at the end of the linked list, and the next reference of the new node points to the head to complete the ring operation
tail.next = node;
tail = tail.next;
tail.next = head;
size++;
}
...
}
The core logic is in the add method. It should be noted that when the linked list is empty, the new node cannot form a ring, that is, the next reference cannot point to itself. Therefore, when adding for the first time, directly point the head and tail to the new node without operating the next reference of the node. When the linked list is not empty, the ring forming step needs to be introduced. The ring forming step is decomposed as follows:
1.tail.next = node
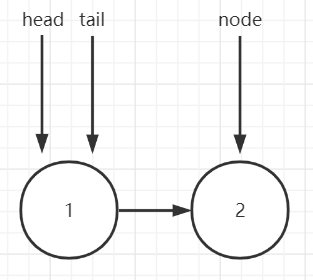
2.tail = tail.next

3.tail.next = head
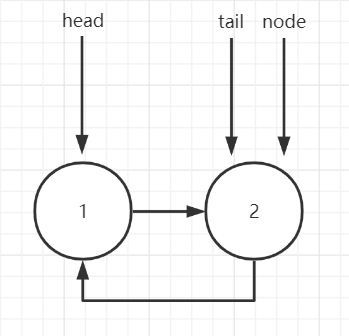
This completes the looping operation.
Test in the main method and construct a circular linked list with a length of 10:
SingleCycleLinkedList singleCycleLinkedList = new SingleCycleLinkedList(10); System.out.println(singleCycleLinkedList);
The results are as follows:
Node{no=1,next=2}, Node{no=2,next=3}, Node{no=3,next=4}, Node{no=4,next=5}, Node{no=5,next=6}, Node{no=6,next=7}, Node{no=7,next=8}, Node{no=8,next=9}, Node{no=9,next=10}, Node{no=10,next=1}
Solve the Joseph problem
Through the previous step, the data storage is completed. Next, we need to solve the problem of how to count cycles. The title requires counting from the k-th person, so you should first find the starting position of counting, and then start the cycle of counting. The person counting to m goes out of the circle, that is, the corresponding node should be removed from the linked list. It should be noted that the nodes of the one-way linked list cannot be deleted by themselves, as shown in the figure:
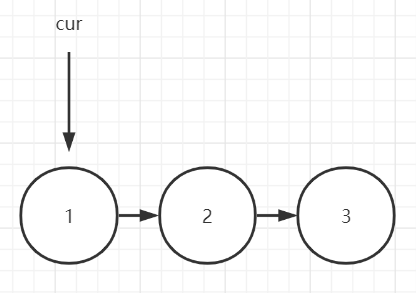
If you want to delete the node numbered 2, the cur reference must point to 1, so that the next reference of 1 can point from the original 2 to 3:
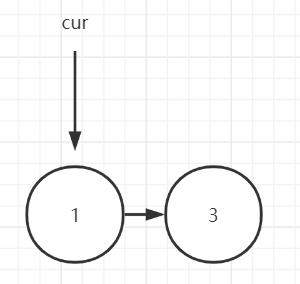
Therefore, when finding the starting position of the number of reports, count from the previous position of the starting position. In this way, when finding the node to be removed, it is actually located to the previous node of the node to be removed. The code for finding the starting position of the alarm is as follows (the start variable in the code is the parameter k):
//Find the node that starts counting (here, start traversing from tail and take the last node of the counting node, because the node deletion of the one-way linked list must depend on the last node)
Node tmp = tail;
int startIndex = 0;
while (startIndex++ != size) {
if (start == startIndex) {
break;
}
tmp = tmp.next;
}
After finding the starting position of the counting, you should start the counting operation. When removing the node, you should note that when there is only one node in the linked list, you do not need to operate the next reference of the node, and you can directly empty the node.
The code for counting out the circle is as follows (the step variable in the code is the parameter m):
//Save order out of chain nodes
List<Node> list = new ArrayList<>(size);
//Start counting. After counting to the specified interval, the node is out of the chain
int count = 1;
while (size > 1) {
if (count == step) {
//Node out of chain
//1. Define a reference to the node to be deleted
Node delNode = tmp.next;
//2. Point the next reference of the current node to the next node of the node to be deleted
tmp.next = delNode.next;
//3. List length - 1
size--;
//4. Empty the next reference of the node to be deleted
delNode.next = null;
//5. Save the deleted node
list.add(delNode);
//6. Reset the counter
count = 1;
} else {
//Continue cycle count
tmp = tmp.next;
count++;
}
}
//When there is only one node left in the linked list, you do not need to operate the next pointer to delete the node, and directly set the head and tail to null
tmp.next = null;
head = null;
tail = null;
size = 0;
list.add(tmp);
Note that after removing nodes, you must ensure that the linked list is still in a ring. The removal steps are broken down as follows (assuming that there are 3 nodes left in the linked list, you should remove the node numbered 3):
1.Node delNode = tmp.next

2.tmp.next = delNode.next
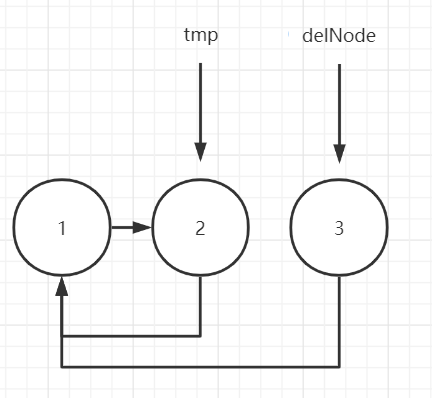
3.delNode.next = null
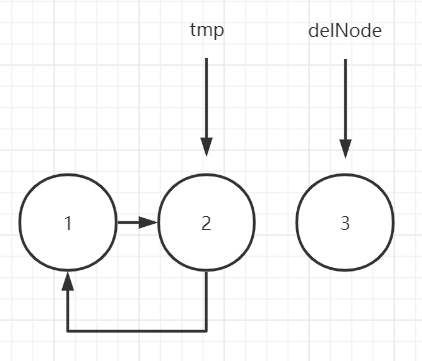
The complete code of counting out circles is as follows:
/**
* Starting from the start position, the node goes out of the chain every step
*
* @param start Start position of alarm
* @param step Count out the lap interval
* @return List the nodes of the chain in turn
*/
public List<Node> poll(int start, int step) {
if (start <= 0 || start > size) {
throw new RuntimeException("The starting position must be greater than 0 and less than or equal to the length of the linked list");
}
if (step <= 0 || step > size) {
throw new RuntimeException("Interval must be greater than 0");
}
if (size == 0) {
return Collections.emptyList();
}
//Find the node that starts counting (here, start traversing from tail and take the last node of the counting node, because the node deletion of the one-way linked list must depend on the last node)
Node tmp = tail;
int startIndex = 0;
while (startIndex++ != size) {
if (start == startIndex) {
break;
}
tmp = tmp.next;
}
//Save order out of chain nodes
List<Node> list = new ArrayList<>(size);
//Start counting. After counting to the specified interval, the node is out of the chain
int count = 1;
while (size > 1) {
if (count == step) {
//Node out of chain
//1. Define a reference to the node to be deleted
Node delNode = tmp.next;
//2. Point the next reference of the current node to the next node of the node to be deleted
tmp.next = delNode.next;
//3. List length - 1
size--;
//4. Empty the next reference of the node to be deleted
delNode.next = null;
//5. Save the deleted node
list.add(delNode);
//6. Reset the counter
count = 1;
} else {
//Continue cycle count
tmp = tmp.next;
count++;
}
}
//When there is only one node left in the linked list, you do not need to operate the next pointer to delete the node, and directly set the head and tail to null
tmp.next = null;
head = null;
tail = null;
size = 0;
list.add(tmp);
return list;
}
Test the above code:
//n: Number of people in the circle, k: the starting position of counting, m: the interval of counting out of the team
int n = 10;
int k = 2;
int m = 3;
List<Node> pollList = singleCycleLinkedList.poll(k, m);
System.out.printf("size: %d, start: %d, step: %d\n", n, k, m);
System.out.println(pollList.stream().map(node -> node.no).collect(Collectors.toList()));
The results are as follows:
size: 10, start: 2, step: 3 [4, 7, 10, 3, 8, 2, 9, 6, 1, 5]
data validation
When n = 10, k = 2, m = 3, the decomposition steps of node removal are as follows:
Complete nodes: Node{no=1}, Node{no=2}, Node{no=3}, Node{no=4}, Node{no=5}, Node{no=6}, Node{no=7}, Node{no=8}, Node{no=9}, Node{no=10}
4 out of loop: Node{no=1}, Node{no=2}, Node{no=3}, Node{no=5}, Node{no=6}, Node{no=7}, Node{no=8}, Node{no=9}, Node{no=10}
7 out of loop: Node{no=1}, Node{no=2}, Node{no=3}, Node{no=5}, Node{no=6}, Node{no=8}, Node{no=9}, Node{no=10}
10 out turn: Node{no=1}, Node{no=2}, Node{no=3}, Node{no=5}, Node{no=6}, Node{no=8}, Node{no=9}
3 out of loop: Node{no=1}, Node{no=2}, Node{no=5}, Node{no=6}, Node{no=8}, Node{no=9}
8 out of loop: Node{no=1}, Node{no=2}, Node{no=5}, Node{no=6}, Node{no=9}
2 out of loop: Node{no=1}, Node{no=5}, Node{no=6}, Node{no=9}
9 out of loop: Node{no=1}, Node{no=5}, Node{no=6}
6 out of loop: Node{no=1}, Node{no=5}
1 out of loop: Node{no=5}
5 out turn
The order of turning is as follows: [4, 7, 10, 3, 8, 2, 9, 6, 1, 5]. Consistent with the results.