Think of every car as a straight line: y = v * t + b

Where v represents speed, t represents time, and b represents initial position

The problem becomes: finding the existence of t makes the y value of the line the largest among all the lines (the same size is allowed)

The specific method is

1. Sort the lines by v (slope)
2. For an ordered line a, b, c, if the intersection of b, c is to the left of the intersection of a, b, round off b

(as shown in the figure, b can never lead)

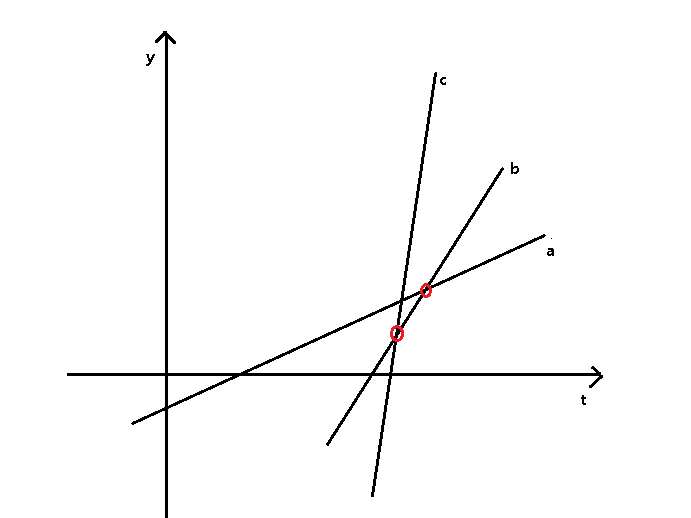
3. Because t > = 0, the case that the intersection point is not in the first quadrant is eliminated.

ps: horizontal coordinate calculation method of intersection of two lines:

y=k1*x+b1　　①

y=k2*x+b2　　②

From ① and ②, it can be concluded that:

k1*x+b1=k2*x+b2

(k1-k2)*x=b2-b1

x=(b2-b1)/(k1-k2)

#include<queue>
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=500010;
int n,sta[maxn],id[maxn],ans[maxn];
struct Car{int b,k,id;}c[maxn];
int top=0,cnt=0;
bool flag[maxn];
bool cmp(const Car &a,const Car &b){
    return a.k<b.k||(a.k==b.k&&a.b>b.b);
}
double getx(int x,int y){
    if (c[y].k-c[x].k==0) return 1e10;
    return (double)((double)c[x].b-c[y].b)/(double)(c[y].k-c[x].k);
}
int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;++i) scanf("%d",&c[i].b);
    for (int i=1;i<=n;++i) scanf("%d",&c[i].k);
    for (int i=1;i<=n;++i) c[i].id=i;
    sort(c+1,c+n+1,cmp);
    sta[++top]=1; id[top]=c[1].id;
    for (int i=2;i<=n;++i){
        if (c[i].k==c[i-1].k&&c[i].b<c[i-1].b) continue;
        while (top>1&&getx(sta[top-1],sta[top])>getx(sta[top],i)) top--;
        sta[++top]=i; id[top]=c[i].id;
    }
    for (int i=2;i<=top;++i)
        if (getx(sta[i-1],sta[i])<0) flag[i-1]=1;
    for (int i=1;i<=top;++i)
        if (!flag[i]) ans[++cnt]=id[i];
    sort(ans+1,ans+cnt+1);
    printf("%d\n",cnt);
    for (int i=1;i<cnt;++i) printf("%d ",ans[i]);
    if (cnt) printf("%d",ans[cnt]);
}