LeetCode 131, number of split palindromes

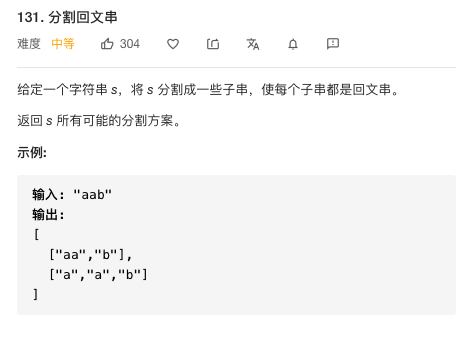
This question is almost the same as the last one yesterday. It is about splitting a string. Therefore, a start index is needed to manage the starting point of the split string. What's more, the storage condition of this question is that the string is the palindrome. In other words, we need to judge whether the split string is a palindrome in the loop Palindromes, if so, will be saved in the list. Then continue to recurse.

class Solution {
     List<List<String>> res =new ArrayList<>();

    public  List<List<String>> partition(String s) {
        if(s.equals("")){
            return res;
        }
        ArrayList<String> lis = new ArrayList<>();
        DFS(s,0,lis);
        return res;
    }
    public  void  DFS(String s,int start,List<String> lis){
        if (start==s.length()){
            ArrayList<String> strings = new ArrayList<>();
            strings.addAll(lis);
            res.add(strings);
        }else {
            for (int i = start; i <s.length() ; i++) {
                String str = s.substring(start, i+1);
                int x=0;
                int y=str.length()-1;
                boolean falg =true;
                while (x<=y){
                    if (str.charAt(x)!=str.charAt(y)) {
                        falg=false;
                        break;
                    }
                    x++;
                    y--;

                }
                if (falg){
                    lis.add(str);
                    DFS(s, i+1, lis);
                    lis.remove(lis.size()-1);
                }

            }
        }
    }
}

LeetCode 7. Combination

The only restriction of this problem is to make sure that the size of the list is k, and let it be the end condition of recursion once,

LeetCode combination

class Solution {
   List<List<Integer>> res1 =new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        if(n<k||k<=0){
            return res1;
        }
        ArrayList<Integer> list = new ArrayList<>();
        combineNum(n, k, 1, list);
        return res1;

    }
    public  void  combineNum(int n,int k,int start,List<Integer> list){
        if (list.size()==k){
            ArrayList<Integer> list1 = new ArrayList<>();
            list1.addAll(list);
            res1.add(list1);
            return;
        }else {
            for (int i = start; i <=n-(k-list.size())+1 ; i++) {
                list.add(i);
                combineNum(n, k, i+1, list);
                list.remove(list.size()-1);
            }
        }
    }
}

class Solution {
    List<List<Integer>> res1 =new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        if(candidates.equals("")||target<=0){
            return res1;
        }
        ArrayList<Integer> list = new ArrayList<>();
        combination(candidates,target,list,0);
        return res1;

    }
    public void combination(int[] candidates,int target,List<Integer> list,int index){
        if(target<=0){
            if(target==0){
                ArrayList<Integer> list1 = new ArrayList<>();
                list1.addAll(list);
                res1.add(list1);
            }
            return;
        }else{
            for(int i =index;i<candidates.length;i++){
                list.add(candidates[i]);
                combination(candidates,target-candidates[i],list,index);
                list.remove(list.size()-1);
                index++;
            }
        }
    }
}

This question is a little different.
What's special is that all elements can be retrieved repeatedly. Of course, we can use the same algorithm structure, and we need to think about traversing the recursive backtracking part.
We find that when a number has been determined, it can still be selected in its sub branches, but in its parallel branches, it can't be selected any more, so we don't need to relocate its cycle start point in the sub branch, but it is the same as the parent node.

LeetCode 40, combined sum

class Solution {
    boolean[] falgs ;
    List<List<Integer>> res1 =new ArrayList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        falgs=new boolean[candidates.length];
        if(candidates.equals("")||target<=0){
            return res1;
        }
        Arrays.sort(candidates);
        ArrayList<Integer> list = new ArrayList<>();
        combination(candidates,target,list,0);
        return res1;

    }
    public void combination(int[] candidates,int target,List<Integer> list,int index){
        if(target<=0||index==candidates.length){
            if(target==0){
                ArrayList<Integer> list1 = new ArrayList<>();
                list1.addAll(list);
                res1.add(list1);
            }
            return;
        }else{
            for(int i =index;i<candidates.length;i++){
                if(i>0&&candidates[i]==candidates[i-1]&&!falgs[i-1]) continue;
              if (!falgs[i]) {
                    list.add(candidates[i]);
                    falgs[i]=true;
                    combination(candidates, target - candidates[i], list, i + 1);
                    list.remove(list.size() - 1);
                    falgs[i]=false;
                }
            }
        }
    }
}

This is an advanced version of the previous question "combination". Why do you say so? Because there may be duplicate elements in this question and it is required that there should be no duplicate combination in the result. I'm sure I'm familiar with this situation when I read the last article. Yes, in this case and what it requires is combination, then we can sort it first, and then solve the problem according to the strategy that the next element of the same element can only keep up with one element at the same time, otherwise we won't judge its branch. Of course, we can judge whether an element is used or not. We still How to use a Boolean array.

LeetCode 216, total number of combinations 3

class Solution {
    List<List<Integer>> res =new ArrayList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        if(n<=0||k<=0){
            return res;
        }
        falgs=new Boolean[10];
        Arrays.fill(falgs,false);
        List<Integer> List= new ArrayList<>();
        combination3(n,k,List,1);
        return res;
        
    }
    public void combination3(int n,int k,List<Integer> list,int start){
        if(list.size()==k){
            if(n==0){
               List<Integer> List1= new ArrayList<>();
               List1.addAll(list);
               res.add(List1);
            }
        }else{
            for(int i=start;i<=9;i++){
                    list.add(i);
                    combination3(n-i,k,list,i+1);
                    list.remove(list.size()-1);
                   
                }
            }   
        }
    }

So what's the difference?
We find that this problem has stipulated that there should be no repeated numbers in the combination, and only 1-9 is allowed, so it is equivalent to let us select k numbers in an array of 1-9 to make the sum of the added numbers equal to n, and these elements can only be selected once. After doing so many problems, we have been very keen to capture that the condition for the end of recursion is the s of the list Whether size is equal to K, and the sub branch also needs to relocate the start position,

LeetCode subset

This question has explained some conditions to us:
Array contains duplicate elements.
The solution set cannot contain the same subset.
This is similar to the above situation, sorting - > judge whether to traverse

class Solution {
    List<List<Integer>> res =new ArrayList<>();
    Boolean[] falgs;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if(nums.length==0){
            return res;
        }
        falgs=new Boolean[nums.length];
        Arrays.sort(nums);
        Arrays.fill(falgs,false);
        List<Integer> list =new ArrayList<>();
        subsets(nums,0,list);
        return res;
    }
    public void subsets(int[] nums,int start,List<Integer> list){
        List<Integer> list1 =new ArrayList<>();
        list1.addAll(list);
        res.add(list1);
        for(int i= start;i<nums.length;i++){
            if(i>0&&nums[i]==nums[i-1]&&!falgs[i-1]) continue;
            if(!falgs[i]){
                list.add(nums[i]);
                falgs[i]=true;
                subsets(nums,i+1,list);
                falgs[i]=false;
                list.remove(list.size()-1);
            }
        }
    }

}

Last question:

Total number of LeetCode binary

class Solution {
    
    public List<String> readBinaryWatch(int num) {
        List<String> List =new ArrayList<>();
        List<Integer> res =new ArrayList<>();
        if(num==0){
           List.add("0:00");
           return List;
        }
        time(List,num,res,0);
        return List;
    }
    public void time(List<String> List ,int num,List<Integer> res,int start){
        if(res.size()==num){
            StringBuilder str =new StringBuilder();
            int h =0;
            int m=0;
            for(int i = 0;i<res.size();i++){
                if(res.get(i)<4){
                    h+=Math.pow(2,res.get(i));
                }else{
                    m+=Math.pow(2,res.get(i)-4);
                }
            }
            if(h>11||m>59) return;
            String xh =h+"";
            str.append(xh);
            str.append(":");
            if(m<10){
                str.append("0");
            }
            String mo=m+"";
            str.append(mo);
            List.add(str.toString());
        }else{
            for(int i =start;i<10;i++){
                res.add(i);
                time(List,num,res,i+1);
                res.remove(res.size()-1);
            }
        }
    }
}

In fact, the idea of this question is very simple. It is still a combination problem. Why do you say so?
The meaning of this question is actually to pick out k lights from these lights and return to the time they represent.
Then we can think of these lights as an array. The array is 0-9, 0-4 is defined as the hour result, followed by the minute result, which can be spliced in the string builder through its operation.
And it should not be difficult for us to pick out k numbers in the array. The same number cannot be selected repeatedly.

class Solution {
    
    public List<String> readBinaryWatch(int num) {
        List<String> List =new ArrayList<>();
        List<Integer> res =new ArrayList<>();
        if(num==0){
           List.add("0:00");
           return List;
        }
        time(List,num,res,0);
        return List;
    }
    public void time(List<String> List ,int num,List<Integer> res,int start){
        if(res.size()==num){
            StringBuilder str =new StringBuilder();
            int h =0;
            int m=0;
            for(int i = 0;i<res.size();i++){
                if(res.get(i)<4){
                    h+=Math.pow(2,res.get(i));
                }else{
                    m+=Math.pow(2,res.get(i)-4);
                }
            }
            if(h>11||m>59) return;
            String xh =h+"";
            str.append(xh);
            str.append(":");
            if(m<10){
                str.append("0");
            }
            String mo=m+"";
            str.append(mo);
            List.add(str.toString());
        }else{
            for(int i =start;i<10;i++){
                res.add(i);
                time(List,num,res,i+1);
                res.remove(res.size()-1);
            }
        }
    }
}

Small summary: the overall structure of these algorithms is almost the same, so we should be able to classify the questions and determine the overall framework by thinking when we do the questions, and then make some changes to the fixed routine in details according to the meaning of the questions. Of course, those who can do pruning should try their best to do pruning. If they are not able to do it, they don't have to force them. For example, I don't want to try pruning first.
Finally, I hope Beijing will get better. Go China.