A catalog

What's the difference between a non-tossing front end and salted fish?

|Directory|
| --- |
| A catalog |
| Second Preface |
| Three problems recurring |
|  3.1 Root Cause: IEEE 754 Standard |
|  3.2 Replication: the calculation process |
|  3.3 Extension: Digital Security |
| 4. Solving problems |
|  4.1 toFixed() |
|  4.2 Handwritten Simple Addition, Subtraction, Multiplication and Division |
| Five ready-made frameworks |
| Six References |

Second Preface

Return to Directory

In everyday work calculations, we're on thin ice, but JavaScript always gives us surprise s like that.

1. 0.1 + 0.2 = ？
2. 1 - 0.9 = ？

If your partner gives you an inner result:

1. 0.1 + 0.2 = 0.3
2. 1 - 0.9 = 0.1

Then the little buddy will be savaged by the fact:

console.log(0.1 + 0.2); // 0.30000000000000004
console.log(1 - 0.9); // 0.09999999999999998

Why is this happening?Let's explore!

Three problems recurring

Return to Directory

Below, we will replicate the problem by discussing the IEEE 754 standard and the JavaScript add-subtract calculation process.

3.1 Root Cause: IEEE 754 Standard

Return to Directory

Numbers in JavaScript use IEEE 754 Standard 64-bit double-precision floating point number.The specification defines the format of floating-point numbers. For 64-bit floating-point numbers, the highest bit is the symbol, the next 11 bits are the exponent, and the remaining 52 bits are valid numbers. Specifically:

• Number 0: Symbol bits.Expressed by s, 0 is positive and 1 is negative.
• Bits 1 - 11: Storage index section.Expressed in e;
• Bits 12 - 63: Store decimal parts (that is, significant numbers).Expressed in f.

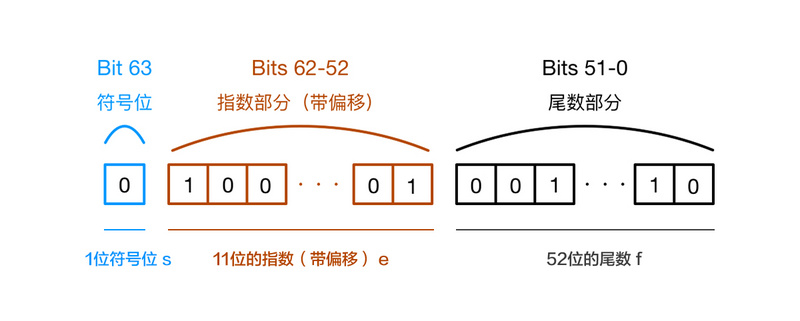
The sign bit determines the positive and negative of a number, the exponential part determines the size of the number, and the decimal part determines the precision of the number.

IEEE 754 specifies that the first significant digit always defaults to 1 and is not stored in a 64-bit floating point number.

That is, valid numbers are always in the form of 1.XX...XX, where the XX...XX portion is stored in 64-bit floating point numbers, possibly up to 52 bits.

Therefore, JavaScript provides up to 53 binary bits of valid numbers (the last 52 bits of a 64-bit floating point + the first 1 of the valid numbers).

3.2 Replication: the calculation process

Return to Directory

What happens when 0.1 + 0.2 is calculated through JavaScript?

1. Replace 0.1 and 0.2 with a binary representation:

0.1 -> 0.0001100110011001... (infinite)
0.2 -> 0.0011001100110011... (infinite)

Floating point numbers are infinite in binary expressions

2. Because the decimal portion of 64-bit double-precision floating-point numbers in the IEEE 754 standard supports a maximum of 53-bit binary bits, the binary value when added together is:

0.0100110011001100110011001100110011001100110011001100

Because of the floating-point decimal limit, this binary number is truncated and converted to decimal, which amounts to 0.30000000000004, resulting in errors in arithmetic calculations.

3.3 Extension: Digital Security

Return to Directory

After looking at the imprecision of the above decimal calculation, jsliang felt it was necessary to talk about integers again because there were also some problems with integers:

console.log(19571992547450991);
// 19571992547450990

console.log(19571992547450991 === 19571992547450994);
// true

Isn't it surprising!

Because Number types in JavaScript are treated as floating-point numbers, integers cannot avoid this problem:

// Maximum
const MaxNumber = Math.pow(2, 53) - 1;
console.log(MaxNumber); // 9007199254740991
console.log(Number.MAX_SAFE_INTEGER); // 9007199254740991

// minimum value
const MinNumber = -(Math.pow(2, 53) - 1);
console.log(MinNumber); // -9007199254740991
console.log(Number.MIN_SAFE_INTEGER); // -9007199254740991

That is, the safe range of integers is: [-9007199254740991, 9007199254740991].

Beyond this range, there is a discarded accuracy problem.

Of course, this problem doesn't just exist in JavaScript. It occurs in almost all programming languages that use the IEEE-745 standard, but in many other languages, methods have been encapsulated to avoid accuracy problems.

• PHP Float Float Float - Manual
• Java Where's your decimal point?- Brian Goetz

Because JavaScript is a weakly typed language, there is no strict data type for floating-point numbers from the design point of view, so the problem of precision error is particularly prominent.

So far, we can see that JavaScript can cause some problems when it comes to manipulating numbers.

In fact, there are real problems at work!

One day I processed a calculation of a worksheet, then the next day I was told there was a problem online, and then I was asked by Miss Product:

• Why can pupils make decimal calculations that your computer can't calculate?

Three seconds of silence, resulting in the above discovery and ultimately the following solutions.

4. Solving problems

Return to Directory

Here are a number of ways to solve floating-point calculations.

4.1 toFixed()

Return to Directory

Parameter: digits.Number of digits after the decimal point; between 0 and 20 (inclusive), the implementation environment may support a larger range.If this parameter is ignored, it defaults to 0.

const num = 12345.6789;

num.toFixed(); // '12346': Round off, excluding decimal parts.
num.toFixed(1); // '12345.7': Round off, leaving one number after the decimal point.
num.toFixed(6); // '12345.678900': Keep the six numbers after the decimal point and fill them with 0 if they are not long enough.
(1.23e+20).toFixed(2); // 123000000000000000000000.00 Scientific Counting becomes a normal number type

The result of toFixed() is the String type, remember to convert the Number type.

The toFixed() method uses a fixed-point representation to format a number and rounds the result.

With toFixed(), we can solve some problems:

Original plus minus multiplier:

console.log(1.0 - 0.9);
// 0.09999999999999998

console.log(0.3 / 0.1);
// 2.9999999999999996

console.log(9.7 * 100);
// 969.9999999999999

console.log(2.22 + 0.1);
// 2.3200000000000003

Use toFixed():

// Formula: parseFloat ((mathematical expression). toFixed(digits));
// toFixed() precision parameter must be between 0 and 20

parseFloat((1.0 - 0.9).toFixed(10));
// 0.1   

parseFloat((0.3 / 0.1).toFixed(10));
// 3  

parseFloat((9.7 * 100).toFixed(10));
// 970

parseFloat((2.22 + 0.1).toFixed(10));
// 2.32

So, when it comes to this, the question arises:

• parseFloat(1.005.toFixed(2))

What do you get? Is your response 1.01?

However, it is not. The result is: 1.

So, enm...fall!o()o

toFixed() proved not to be the safest solution.

4.2 Handwritten Simple Addition, Subtraction, Multiplication and Division

Return to Directory

Since JavaScript's own methods are not self-saving, we can only think differently:

• Convert decimal parts of JavaScript to strings for calculation

/**
 * @name Detect whether data is overrun
 * @param {Number} number 
 */
const checkSafeNumber = (number) => {
  if (number > Number.MAX_SAFE_INTEGER || number < Number.MIN_SAFE_INTEGER) {
    console.log(`number ${number} Overrun, please note the risk!`);
  }
};

/**
 * @name Correct Data
 * @param {Number} number Numbers requiring correction
 * @param {Number} precision Positive digits
 */
const revise = (number, precision = 12) => {
  return +parseFloat(number.toPrecision(precision));
}

/**
 * @name Get the length after the decimal point
 * @param {Number} Numbers to be converted
 */
const digitLength = (number) => {
  return (number.toString().split('.')[1] || '').length;
};

/**
 * @name Remove decimal points from numbers
 * @param {Number} Numbers to be converted
 */
const floatToInt = (number) => {
  return Number(number.toString().replace('.', ''));
};

/**
 * @name Accuracy Calculation Multiplication
 * @param {Number} arg1 Multiplier 1
 * @param {Number} arg2 Multiplier 2
 */
const multiplication = (arg1, arg2) => {
  const baseNum = digitLength(arg1) + digitLength(arg2);
  const result = floatToInt(arg1) * floatToInt(arg2);
  checkSafeNumber(result);
  return result / Math.pow(10, baseNum);
  // Dividing two integers within the safe range of integers is OK
  // If so, show me the proof
};

console.log('------\n Multiplication:');
console.log(9.7 * 100); // 969.9999999999999
console.log(multiplication(9.7, 100)); // 970

console.log(0.01 * 0.07); // 0.0007000000000000001
console.log(multiplication(0.01, 0.07)); // 0.0007

console.log(1207.41 * 100); // 120741.00000000001
console.log(multiplication(1207.41, 100)); // 0.0007

/**
 * @name Accuracy calculation addition
 * @description JavaScript Error in addition result, two floating point numbers 0.1 + 0.2!== 0.3, this method can remove the error.
 * @param {Number} arg1 Plus 1
 * @param {Number} arg2 Plus 2
 * @return arg1 + arg2
 */
const add = (arg1, arg2) => {
  const baseNum = Math.pow(10, Math.max(digitLength(arg1), digitLength(arg2)));
  return (multiplication(arg1, baseNum) + multiplication(arg2, baseNum)) / baseNum;
}

console.log('------\n Addition:');
console.log(1.001 + 0.003); // 1.0039999999999998
console.log(add(1.001, 0.003)); // 1.004

console.log(3.001 + 0.07); // 3.0709999999999997
console.log(add(3.001, 0.07)); // 3.071

/**
 * @name Accuracy subtraction
 * @param {Number} arg1 Minus 1
 * @param {Number} arg2 Minus 2
 */
const subtraction = (arg1, arg2) => {
  const baseNum = Math.pow(10, Math.max(digitLength(arg1), digitLength(arg2)));
  return (multiplication(arg1, baseNum) - multiplication(arg2, baseNum)) / baseNum;
};

console.log('------\n Subtraction:');
console.log(0.3 - 0.1); // 0.19999999999999998
console.log(subtraction(0.3, 0.1)); // 0.2

/**
 * @name Precision calculation Division
 * @param {Number} arg1 Divider 1
 * @param {Number} arg2 Divider 2
 */
const division = (arg1, arg2) => {
  const baseNum = Math.pow(10, Math.max(digitLength(arg1), digitLength(arg2)));
  return multiplication(arg1, baseNum) / multiplication(arg2, baseNum);
};

console.log('------\n Division:');
console.log(0.3 / 0.1); // 2.9999999999999996
console.log(division(0.3, 0.1)); // 3

console.log(1.21 / 1.1); // 1.0999999999999999
console.log(division(1.21, 1.1)); // 1.1

console.log(1.02 / 1.1); // 0.9272727272727272
console.log(division(1.02, 1.1)); // Number 927272727272 is over limit, please note the risk!0.92727272727272

console.log(1207.41 / 100); // 12.074100000000001
console.log(division(1207.41, 100)); // 12.0741

/**
 * @name Rounding by specified number of digits
 * @param {Number} number Numbers to choose from
 * @param {Number} ratio How many decimal places exactly
 */
const round = (number, ratio) => {
  const baseNum = Math.pow(10, ratio);
  return division(Math.round(multiplication(number, baseNum)), baseNum);
  // Is there a problem with rounding one decimal place after Math.round(), and if so, prove it
  // https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/Math/round
}

console.log('------\n Rounding:');
console.log(0.105.toFixed(2)); // '0.10'
console.log(round(0.105, 2)); // 0.11

console.log(1.335.toFixed(2)); // '1.33'
console.log(round(1.335, 2)); // 1.34

console.log(-round(2.5, 0)); // -3
console.log(-round(20.51, 0)); // -21

In this code, we first calculate by multiplying the stone hammer, and then convert the number to an integer, resulting in safe data.

Will JavaScript integer operations work?

After the multiplication is calculated, assume that the multiplication is OK, and then use the multiplication to deduce the three operations of addition, subtraction and division.

Finally, the rules for rounding are made by multiplication and division.

Is there anything wrong with the numbers generated by JavaScript Math.round()?

In this way, we have worked out the addition, subtraction, multiplication, division and rounding of two numbers (keeping the specified length), so will there be any problem?

If so, please cite.

If not, can you add, subtract, multiply and divide three or more numbers according to the addition, subtraction and division of the above two numbers?

Five ready-made frameworks

Return to Directory

With such important calculations, you will always feel panic and crisis-ridden if you write your own.

So many times, we can use the JavaScript calculation libraries written by the big guys, because the big guys have done a lot of testing for us, which greatly reduces the problems with our handwriting, so we can call the class libraries written by others.

Here are some good libraries to recommend:

• Math.js.

Math.js is an extended math library for JavaScript and Node.js.

It has flexible expression parsers that support symbolic computation, a large number of built-in functions and constants, and provides integrated solutions to handle different data types, such as numbers, large numbers, complex numbers, fractions, units, and matrices.

Powerful and easy to use.

• decimal.js

Any precision decimal type of JavaScript.

• big.js

A small, fast, easy-to-use library for decimal arithmetic operations with arbitrary precision.

• bignumber.js

A JavaScript library for arbitrary precision arithmetic.

Finally, it is worth mentioning that if the calculation of numbers is very strict, you may be able to throw parameters to the back end, let the back end do the calculation, and return the results to you.

For example, calculations involving bitcoins, store commodity prices, etc. ~

Six References

Return to Directory

In honor of the big guys who have contributed to the field of JavaScript computing, this article uses the following articles in general to try and merge them personally, and thanks for their literature:

• JavaScript Floating Point Trap and Solution--camsong
• <GitHub number-precision - nefe>
• "Floating Point Accuracy in JS--Xie Xiaofei"
• Precision Issues for JavaScript Floating Point Operations - WEB Front End Development
• PHP Float Float Float - Manual
• Java Where's your decimal point?- Brian Goetz

If you want to know more, please pay attention to jsliang's document library: document-library

<img alt="Knowledge Sharing License Agreement" style="border-width:0" src="https://user-gold-cdn.xitu.io/2019/11/21/16e8ba77d56b35d5?W=88&h=31&f=png&s=1888"/>
<span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">jsliang's document library</span> Liang Junrong Use Knowledge Sharing Attribution-Non-Commercial Use-Sharing 4.0 International License Agreement in the Same Way License.
Be based on https://github.com/LiangJunro... Creation of works on.
Use rights other than those authorized under this License Agreement may be https://creativecommons.org/l... Get it everywhere.