Preface
-
Immediately after what was said Implementation of Binary Tree and Traversal of Binary Trees Today, let's talk about using javascript to find and delete binary trees.
-
To make it look awkward to read on the surface, omit Node with Node Value x directly from Node X in the following
-
The following first introduces the implementation and traversal of binary trees, where the implementation of binary trees is modified a little:
// Node object function Node(data, right, left) { this.data = data; this.left = left; this.right = right; } // Binary Tree Object function BST() { this.root = null; } // Insert Binary Tree BST.prototype.insert = function(data) { var node = new Node(data, null, null); if(this.root == null) { this.root = node; } else { var current = this.root; while(true) { if(data < current.data) { if(current.left == null) { current.left = node; break; } else { current = current.left; } } else { if(current.right == null) { current.right = node; break; } else { current = current.right; } } } } }; // Intermediate traversal BST.prototype.inOrder = function(node, callback) { if(node != null) { this.inOrder(node.left, callback); callback && callback(node.data); this.inOrder(node.right, callback); } }; // Preorder traversal BST.prototype.preOrder = function(node, callback) { if(node != null) { callback && callback(node.data); this.preOrder(node.left, callback); this.preOrder(node.right, callback); } }; // Post-order traversal BST.prototype.postOrder = function(node, callback) { if(node != null) { this.postOrder(node.left, callback); this.postOrder(node.right, callback); callback && callback(node.data); } };
Binary Tree Lookup
The course of finding binary trees is simply divided into:
- Find the maximum and minimum values of a binary tree;
- The given value is found in the binary tree.
Find Maximum and Minimum
Have seen Implementation of Binary Tree Or someone who already has a related data structure will know that it is very simple to implement.The minimum value is the leftmost leaf node of the binary tree, and the maximum value is the leftmost leaf node of the binary tree.
BST.prototype.getMin = function() { var current = this.root; while(current.left != null) { current = current.left; } return current.data; }; BST.prototype.getMax = function() { var current = this.root; while(current.right != null) { current = current.right; } return current.data; };
Exceptionally simple!
Code test:
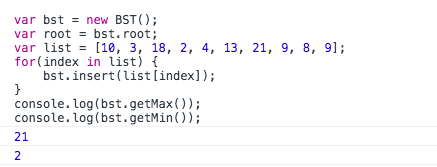
Find a given value
One characteristic of a binary tree is that the left node value < the parent node value < the right node value
This leads to three scenarios:
- The node value is equal to the given value=>Returns the node;
- Given value <node value=>Find the left node of the current node and compare it with the given value.
- Given value>Node value=>Find the right node of the current node and compare it with the given value;
PS: To put it plainly, compare with each node one by one, starting from the root node, with a given value, then equal returns, greater than finds right, less than finds left, until equal or no longer finds.
BST.prototype.find = function(data) { var current = this.root; while(current) { if(current.data == data) { return current; } else if(data < current.data) { current = current.left; } else{ current = current.right; } } return null; };
It's also very simple!

Deletion of Binary Tree Nodes
The deletion of a binary tree node can also be divided into several cases:
- The deleted node is a leaf node;
- The deleted node has only one child node (subtree);
- Deleted node has two children (subtree)
Deleted node is a leaf node
Idea: Set the reference value of the child node pointed to by the parent of the leaf node to be empty
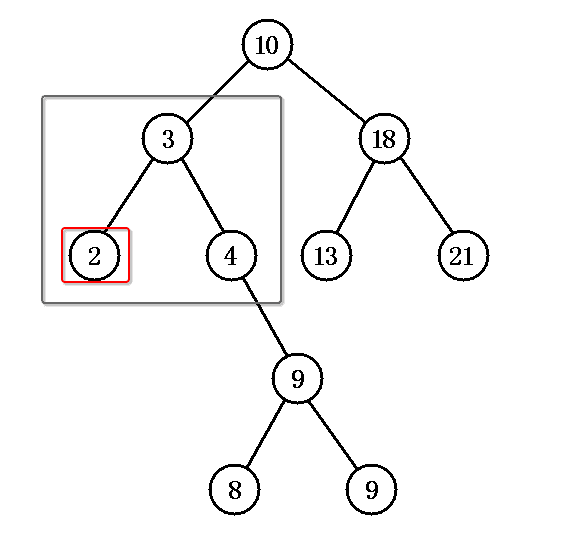
As an example, delete Node 2
console.log(node.data); // 3 // Delete Node 2 node.letf = null;
Deleted node has only one subtree
Idea: Change the reference to the parent node of the node to the child node of the node.
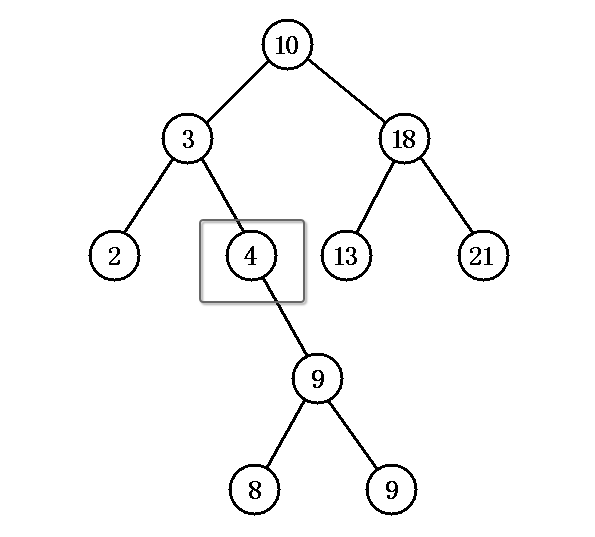
As an example, delete Node 4.Change node.right of node 3 to node.letf =node 9
The deleted node has two subtrees
Think: There are two ways to deal with this situation:
- Find node A with the largest value from the left subtree of the node to be deleted, replace the node to be deleted, and delete node A;
- Find node A with the smallest value from the right subtree of the node to be deleted, replace the node to be deleted, and delete node A.
PS: Here we choose the second method.
As an example of a binary tree in the following figure, delete node 3.
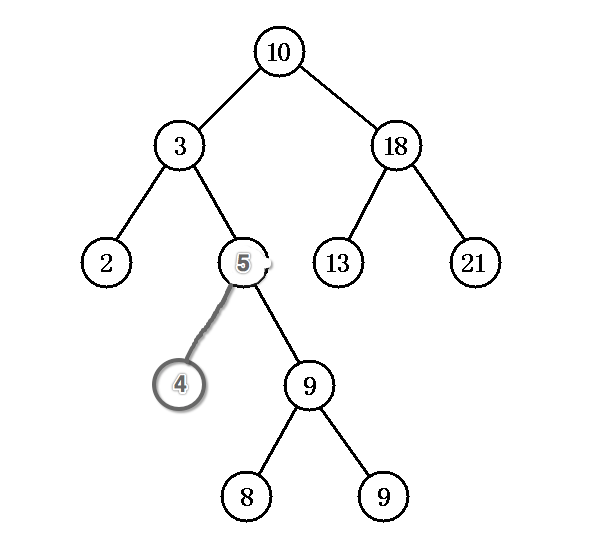
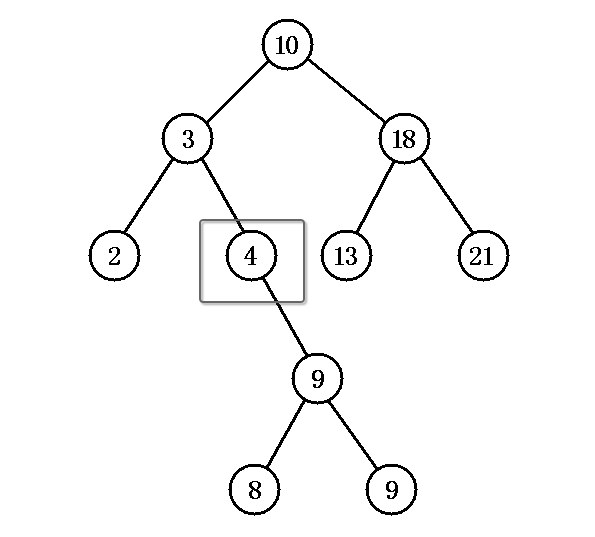
According to the above ideas, the first is to find the node with the smallest node value in the right subtree of node 3. We can see from manual artificial intelligence that node 4 is what we are looking for. In fact, it is easy to find the node because it is small on the right and large on the left of the binary tree.Then replace node 5 with node 4, and delete the node with the minimum value that the node just found.The end result is:
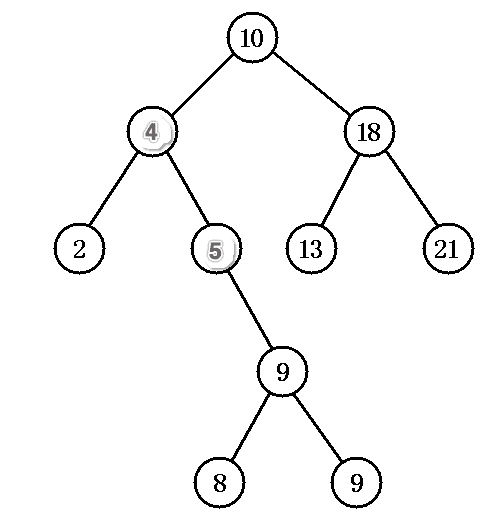
See me change the picture, change it to make people understand better, never avoid pits.
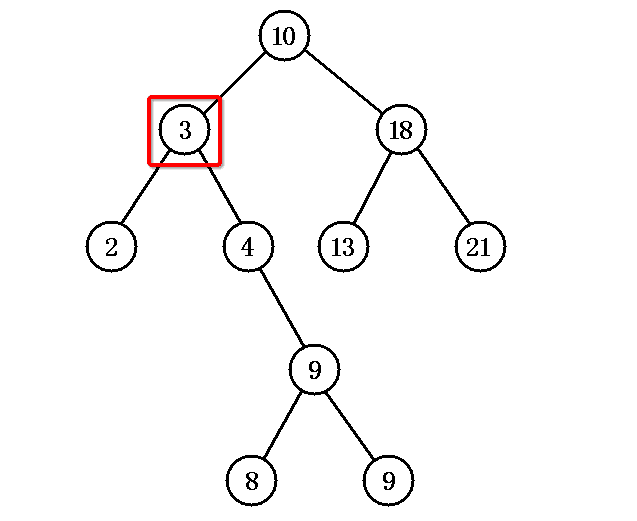
It also deletes node 3, replaces it with node 4, and becomes:
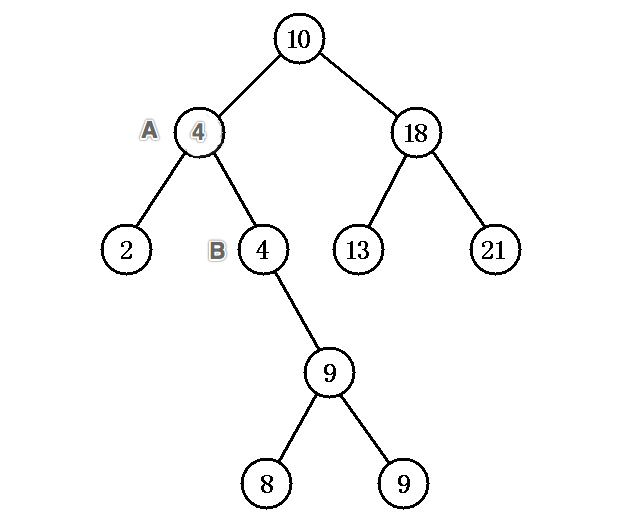
As mentioned above, to delete node B with the smallest node value found, does deleting node B feel a little familiar, or is it the case that the deleted node has only one subtree? [Cover your face], in fact, has it been found that it is quicker to replace node with node value of 2 to node with one that has a deadline of 3?
All three scenarios are finished, to see the specific implementation of the code:
// Gets the minimum binary tree value under a given node BST.prototype.getSmallest = function(node) { if(node.left == null) { return node; } else { return getSmallest(node.left); } }; // Delete the corresponding node of a binary tree under a given node BST.prototype.removeNode = function(node, data) { if(node == null) { return null; } if(data == node.data) { // No child nodes (subtrees) if(node.left == null && node.right == null) { return null; } // Only right child nodes (subtrees) else if(node.left == null ) { return node.right; } // Only left child nodes (subtrees) else if(node.right == null){ return node.left; } // There are two child nodes (subtree) else { var tempNode = this.getSmallest(node.right); node.data = tempNode.data; node.right = this.removeNode(node.right, tempNode.data); return node; } } else if(data < node.data) { node.left = this.removeNode(node.left, data); return node; } else { node.right = this.removeNode(node.right, data); return node; } }
As you can see above, both methods are implemented recursively.The clever thing about removeNode recursion is return, for example, node.right = this.removeNode(node.right, data); this sentence assumes that the deleted node is node 4
You will find that this.removeNode(node.left, data) executes the following code:
else if(node.left == null ) { return node.right; }
Take a look at the code, and the final code is: node.right = node.right.right; the node.right is deleted "unintentionally" and can be replaced with Delete Node 4.Node is Node 3, node.rightis Node 4, and node.right.rightis Node 9.
Finally, let's test the code:
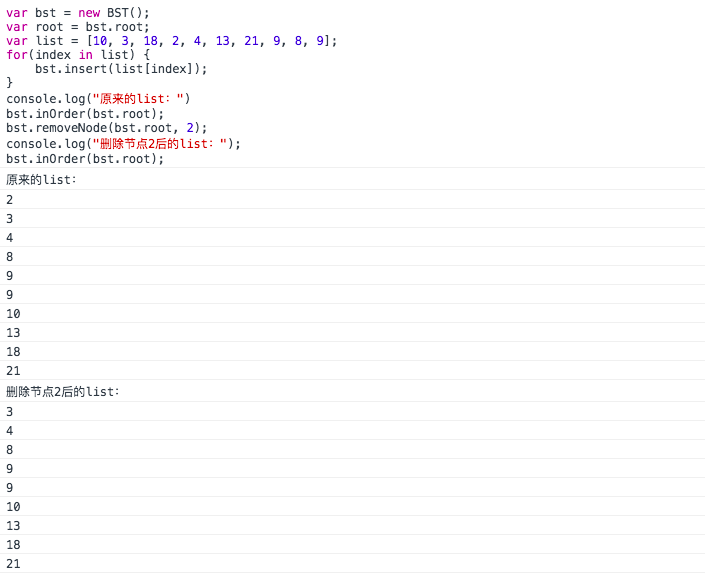
Master Audiences, let's talk about this first, and then the next embarrassing blog.