1. Implementation of ES6 simulation stack

let Stack = (function() {
  const items = new WeakMap();   // Put it into WeakMap for unified management to avoid direct external modification of data
  class Stack {
    constructor() {
      items.set(this, [])
    }
    push(element) {
      items.get(this).push(element);
      return items.get(this);
    }

    pop() {
      return items.get(this).pop();
    }

    isEmpty() {
      return items.get(this).length === 0;
    }

    size() {
      return items.get(this).length;
    }

    peer() {
      let s = items.get(this);
      return s[s.length - 1];
    }

    clear() {
      let s = items.get(this);
      items.set(this, []);
    }
    print() {
        console.log(this.toString());
    }

    toString() {
      return items.get(this).toString();
    }
  }
  return Stack;
})();

2. Base conversion of stack application

Problem Description: convert decimal to other decimal data.

function baseConverter(decNumber, base){

    var remStack = new Stack(),
        rem,
        baseString = '',
        digits = '0123456789ABCDEF';

    while (decNumber > 0){
        rem = Math.floor(decNumber % base);
        remStack.push(rem);
        decNumber = Math.floor(decNumber / base);
    }

    while (!remStack.isEmpty()){
        baseString += digits[remStack.pop()];
    }

    return baseString;
}

3. Bracket matching of stack application

Problem Description: the bracket format should be correct, and no syntax error is formed.

function isBracketBalanced(str) {
  let stack = new Stack(),
      i;
  if (!/^[(|)]*$/.test(str)) {
    throw new Error("the str can only contain '(' or ')'");
  }    // If it contains characters other than brackets, an error is reported
  for (i = 0; i < str.length; i++) {
    if (str[i] === '(') {
      stack.push('(');
    } else {
      if (!stack.pop()) {
        return false;
      }
    }
  }
  return stack.isEmpty();
}

// test
var res = isBracketBalanced('(((()())(())))(');
console.log(res);

4. Hanoi Tower in stack application

Problem Description: there are three columns and a set of hollow disks with different diameters on the tower. At the beginning, all the disks on the source column are arranged from large to small. The goal is to move one disk to another column at a time, and finally move a bunch of disks to the target column. In the process, it is not allowed to place the larger disk on the smaller disk.

The moving process of three plates: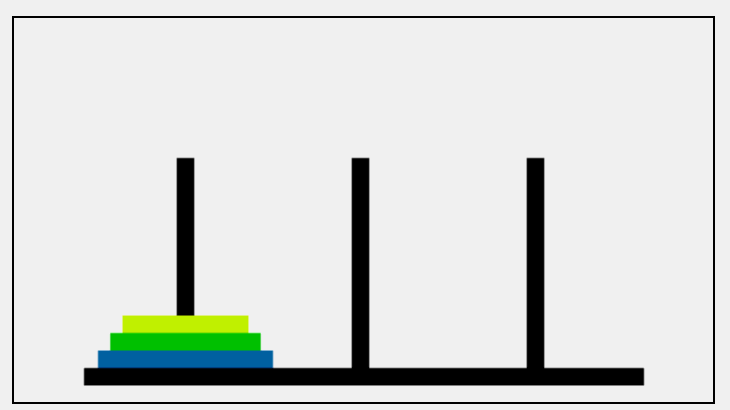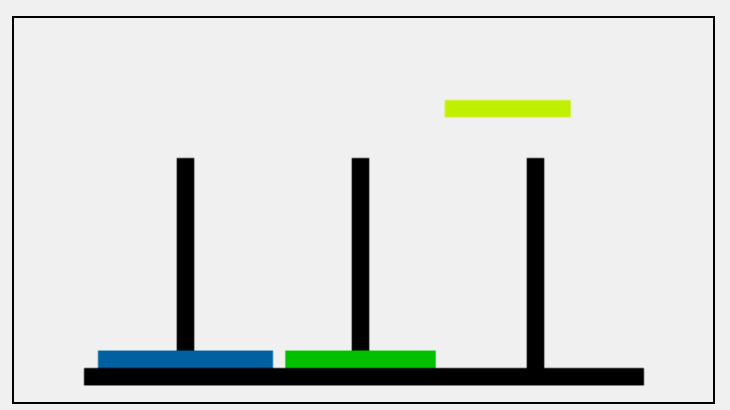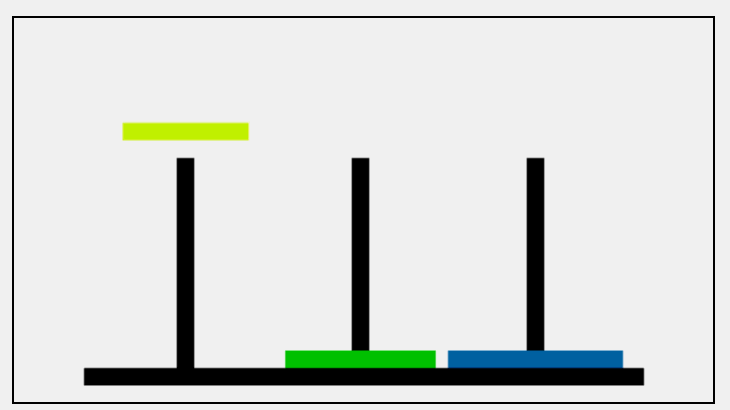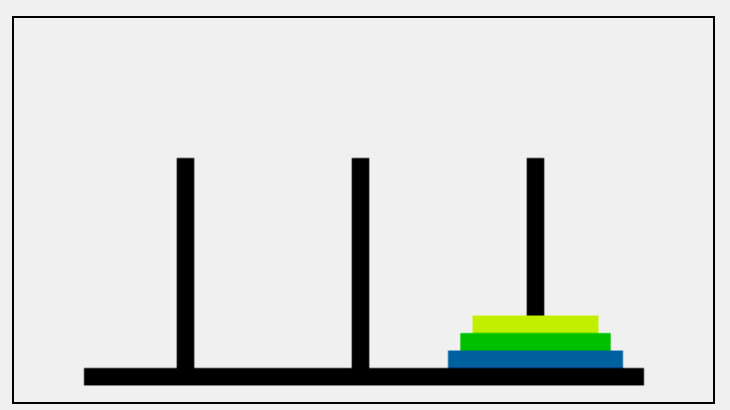

When N plates, only recursion can be used. The idea is as follows: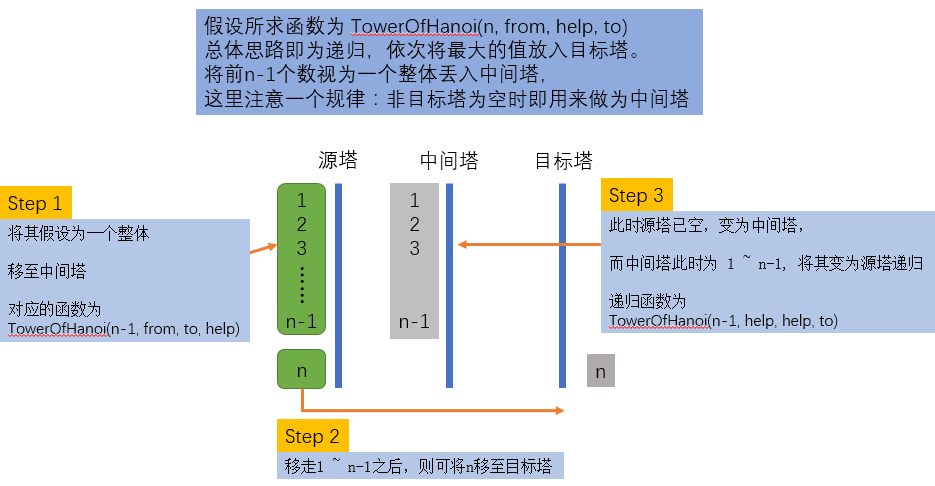

Code implementation:

var towerOfHanoi = function(n, from, help, to) {
  if (n > 0) {
    towerOfHanoi(n-1, from, to, help);
    to.push(from.pop());
    console.log('----------------');
    from.print();
    help.print();
    to.print();
    towerOfHanoi(n-1, help, from, to);

  }
}

var a = new Stack(),
    b = new Stack(),
    c = new Stack(),
    n = 10;

for(let i = n; i > 0; i--) {
  a.push(i);
}
// test
towerOfHanoi(a.size(), a, b, c);