Java - time complexity and space complexity

The time complexity and space complexity of common sorting algorithms are as follows:

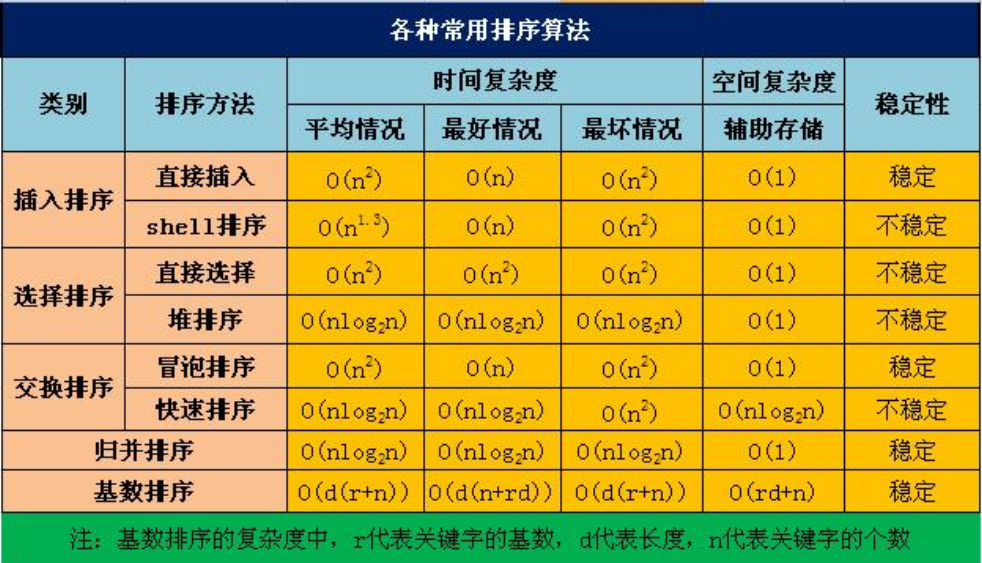
1. Algorithm efficiency

There are two kinds of algorithm efficiency analysis:
The first is time efficiency and the second is space efficiency. Time efficiency is called time complexity, and space efficiency is called space complexity. Time complexity mainly measures the running speed of an algorithm, while space complexity mainly measures the additional space required by an algorithm. In the early stage of computer development, the storage capacity of the computer is very small. So I care about the complexity of space. However, with the rapid development of computer industry, the storage capacity of computer has reached a high level. Therefore, we no longer need to pay special attention to the spatial complexity of an algorithm

2. Time complexity

2.1 concept of time complexity

The time spent by an algorithm is directly proportional to the execution times of the statements in it. The execution times of the basic operations in the algorithm is the time complexity of the algorithm.

2.2 progressive representation of large O

// Please calculate how many times func1 basic operations have been performed?
void func1(int N){
    int count = 0;
    for (int i = 0; i < N ; i++) {
        for (int j = 0; j < N ; j++) {
        count++;
        }
    }
    for (int k = 0; k < 2 * N ; k++) {
       count++;
    }
    int M = 10;
    while ((M--) > 0) {
        count++;
    }
    System.out.println(count);
}

Number of basic operations performed by Func1:

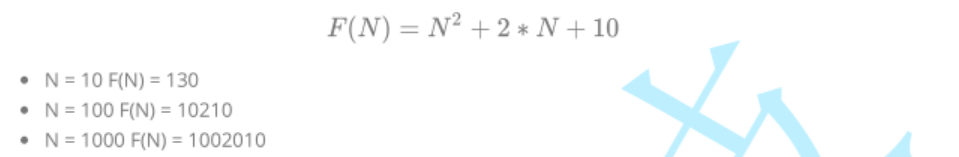
In fact, when we calculate the time complexity, we do not have to calculate the exact execution times, but only the approximate execution times. Here, we use the asymptotic representation of large O
Big O notation: a mathematical symbol used to describe the asymptotic behavior of a function.
Principle of large order O method:
1. Replace all addition constants in the run time with constant 1.
2. In the modified run times function, only the highest order term is retained.
3. If the highest order term exists and is not 1, the constant multiplied by this item is removed. The result is large O-order.
After using the progressive representation of large O, the time complexity of Func1 is:

From the above, we can find that the progressive representation of big O removes those items that have little impact on the results, and succinctly represents the execution times.
In addition, the time complexity of some algorithms has the best, average and worst cases:
Worst case: maximum number of runs of any input scale (upper bound)
Average case: expected number of runs of any input scale
Best case: minimum number of runs of any input scale (lower bound)
For example, search for a data x in an array of length N
Best case: 1 time
Worst case: found N times
Average: N/2 times
In practice, we usually focus on the worst-case operation of the algorithm, so the time complexity of searching data in the array is O(N)

2.3 common time complexity calculation examples

Example 1:

// Calculate the time complexity of func2?
void func2(int N) {
    int count = 0;
    for (int k = 0; k < 2 * N ; k++) {
     count++;
    }
    int M = 10;
    while ((M--) > 0) {
     count++;
    }
    System.out.println(count);
}

Example 2:

// Calculate the time complexity of func3?
void func3(int N, int M) {
    int count = 0;
    for (int k = 0; k < M; k++) {
        count++;
    }
    for (int k = 0; k < N ; k++) {
        count++;
    }
    System.out.println(count);
}

Example 3:

// Calculate the time complexity of func4?
void func4(int N) {
    int count = 0;
    for (int k = 0; k < 100; k++) {
    count++;
    }
    System.out.println(count);
}

Example 4:

// Calculate the time complexity of bubbleSort?
void bubbleSort(int[] array) {
    for (int end = array.length; end > 0; end--) {
    boolean sorted = true;
    for (int i = 1; i < end; i++) {
        if (array[i - 1] > array[i]) {
        Swap(array, i - 1, i);
        sorted = false;
        }
    }
        if (sorted == true) {
            break;
        }
    }
}

Example 5:

// Calculate the time complexity of binarySearch?
int binarySearch(int[] array, int value) {
    int begin = 0;
    int end = array.length - 1;
    while (begin <= end) {
        int mid = begin + ((end-begin) / 2);
        if (array[mid] < value)
            begin = mid + 1;
        else if (array[mid] > value)
            end = mid - 1;
        else
        return mid;
    }
    return -1;
}

Example 6:
be careful:
Time complexity of recursion = Times of recursion * times of execution of each recursion

// The time complexity of computing factorial recursive factorial?
long factorial(int N) {
    return N < 2 ? N : factorial(N-1) * N;
}

Example 7:

// Computing the time complexity of fibonacci recursive fibonacci?
int fibonacci(int N) {
    return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}

Example answer and analysis:

The basic operation of example 1 was performed 2N+10 times. It is known that the time complexity is O(N) by deriving the large O-order method
The basic operation of example 2 is executed M+N times, with two unknowns M and N, and the time complexity is O(N+M)
The basic operation of example 3 is performed 100 times. By deriving the large O-order method, the time complexity is O(1)
In example 4, the basic operation was performed for the best N times and the worst (N*(N-1))/2 times. By deriving the large O-order method + time complexity, it is generally the worst, and the time complexity is O(N^2)
In example 5, the basic operation is performed for the best time and the worst time O(logN) times. The time complexity is O(logN) ps: logN is expressed as base 2 and logarithm N in algorithm analysis. Some places will be written as lgN. (it is recommended to explain how logN is calculated through origami search) (because half of the unsuitable values are excluded each time for binary search, one score is left: n/2, two scores are left: n/2/2 = n/4)
In example 6, through calculation and analysis, it is found that the basic operation recurses N times and the time complexity is O(N).
In Example 7, through calculation and analysis, it is found that the basic operation recurses 2^N times, and the time complexity is O (2^N). (it is recommended to draw a binary tree of recursive stack frames)

3. Space complexity

Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. Space complexity is not how many bytes the program occupies, because it doesn't make much sense, so space complexity is the number of variables. The calculation rules of spatial complexity are basically similar to the practical complexity, and the large O asymptotic representation is also used.

3.1 common time complexity calculation examples