catalogue
Basic idea of selective sorting
swap exchange mode
Bit operations are mainly for integers, mathematical calculations are mainly for decimals and integers, and arrays are the most commonly used.
- Bit operation, two digit XOR processing
- Mathematical calculation
- Through array exchange
Bit operation
XOR ^
Convert the number into binary form. The corresponding two numbers (0 / 1) are the same, and the result is 0. If they are different, the result is 0
| a = a^b | 0100 0011 0111 | a=7(0111) |
| b = a^b | 0111 0011 0100 | b = 4 |
| a = a^b | 0111 0100 0011 | a = 5 |
private static <T> void swap3 (int[] element,int index1,int index2){
element[index1] = element[index1]^element[index2];
element[index2] = element[index1]^element[index2];
element[index1] = element[index1]^element[index2];
}
Mathematical calculation
a: 4 b: 5
a = a + b a = 9 b = 5
b = a - b a = 9 b = 4
a = a - b a = 5 b = 4
private static<T extends Number> void swap2(int[] element,int index1,int index2){
// Mathematical calculation
element[index1] = element[index1]+element[index2];
element[index2] = element[index1]-element[index2];
element[index1] = element[index1]-element[index2];
}Through array exchange
Define the intermediate variable temp exchange.
private static <T> void swap1 (T[] element,int index1,int index2){
T temp = element[index1];
element[index1] = element[index2];
element[index2] = temp;
}You can't write like this. The formal parameters don't affect the arguments, and the results are not exchanged.
public static void swap(int a,int b){
int temp = a;
a = b;
b = temp;
}
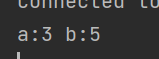
public static void main(String[] args) {
int a = 3;
int b = 5;
swap(a,b);
System.out.println("a:"+a+ " b:"+b);
}
Bubble sorting
Bubble sorting is stable.
Basic idea of bubble sorting
First trip: compare the first number with the second number, with the small one in the front and the large one in the back; The second number is compared with the third number, with the small one in the front and the large one in the back; Compare to the last two numbers in turn. The last number is the largest of all numbers.
The second trip: compare the first number with the second number, with the small one in the front and the large one in the back; The second number is compared with the third number, with the small one in the front and the large one in the back; Compare to the penultimate number and the penultimate number in turn; The penultimate number will be obtained.
······
The nth trip: compare the first number with the second number; Sort complete.
Optimization of bubble sorting:
Define a boolean variable flag, which is inside the outer loop and outside the inner loop. If the inner loop is completed in turn, the flag is true, otherwise it is false. If the inner loop is not exchanged, it indicates that the internal sorting is completed, and the flag has not changed. If it is false, break and jump out of the outer loop.
Sort complete.
Code design
Complete with double circulation: the external circulation variable is represented by i, and the internal circulation variable is set to j. assuming a total of N numbers, the external circulation is n-1 times, and each time of the internal circulation is (n-1, n-2, n-3, ····, 2, 1), that is, (elemnet.length - i -1) times. The number of each two comparisons is related to the inner loop j, expressed as element [j] and element [j+1].
code implementation
public class bubbleSort {
public static<T extends Comparable<T>> void BubbleSort(T[] element){
// If the array is empty or the length of the array is 1, return directly
if(element == null || element.length == 1){
return;
}
for(int i = 0;i <element.length-1;i++){
// Flag is a flag, which is initially false. If there is no data exchange in this sorting, the sorting completion flag is false and the cycle exits
boolean flag = false;
for(int j = 0;j < element.length-i-1;j++){
if(element[j].compareTo(element[j+1]) > 0){ // The former is greater than the latter
swap1(element,j,j+1);
flag = true;
}
}
if(!flag){
break; // Exit loop
}
}
}
private static <T> void swap1 (T[] element,int index1,int index2){
T temp = element[index1];
element[index1] = element[index2];
element[index2] = temp;
}
public static void main(String[] args) {
Integer[] array = new Integer[]{1,4,5,7,2,3,6,8};
BubbleSort(array);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
}
}Time and space complexity
Space complexity: O(1) No new memory space was opened up
Time complexity: O(N^2)
Optimal time complexity: O(N) , When the sequence approaches and is completely ordered.
This condition is met in two cases:
- three four five 7. Exit after traversing. Traversal times n-1;
- four three five 7. The first traversal, the first two numbers exchange, the second traversal, completely orderly, exit. (n-1)+(n-2)
Select sort
Selection sorting is unstable.
Basic idea of selective sorting
The sequence is divided into ordered sequence and unordered sequence. Each time the unordered list is traversed, when the smallest one is found, the smallest number is exchanged with the first bit of the unordered sequence, and the first bit of the unordered sequence after exchange becomes an ordered sequence.
- In the initial state, the sequence is disordered and the ordered sequence is empty.
- The first traversal, find the smallest number, exchange with the first bit of the current sequence, and the first bit is classified as an ordered sequence. Followed by unordered sequences
- The second traversal starts from the second digit (i.e. unordered sequence), finds the smallest digit, and exchanges with the first digit of unordered sequence. The first two digits are ordered sequence, followed by unordered sequence.
- ......
- ......
- ......
- The n-1 traversal determines the size of the last two numbers
Code design
Double loop completion is used. i controls the number of times and j controls the number of times of each traversal comparison
Define the subscript minIndex of the minimum value, and the initial minIndex = i; When a subsequent number is less than minIndex, the minIndex is updated to j (the subscript of the smaller number)
After the traversal is completed, the exchange subscripts are i and The value of minIndex.
code implementation
public static<T extends Comparable<T>> void selectSort(T[] element){
if(element == null || element.length == 1){
return;
}
for(int i=0;i< element.length;i++){
int minIndex = i;
for(int j = i; j< element.length;j++){
if(element[j].compareTo(element[minIndex]) < 0){
minIndex = j;
}
}
swap(element,minIndex,i);
}
}
private static <T> void swap (T[] element,int index1,int index2){
T temp = element[index1];
element[index1] = element[index2];
element[index2] = temp;
}
public static void main(String[] args) {
Integer[] arr = new Integer[]{1,4,6,3,2,7};
selectSort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}Time and space complexity
Space complexity: O(1) No new memory space was opened up
Average time complexity: O(N^2)
Optimal time complexity: O(N^2)
Insert sort
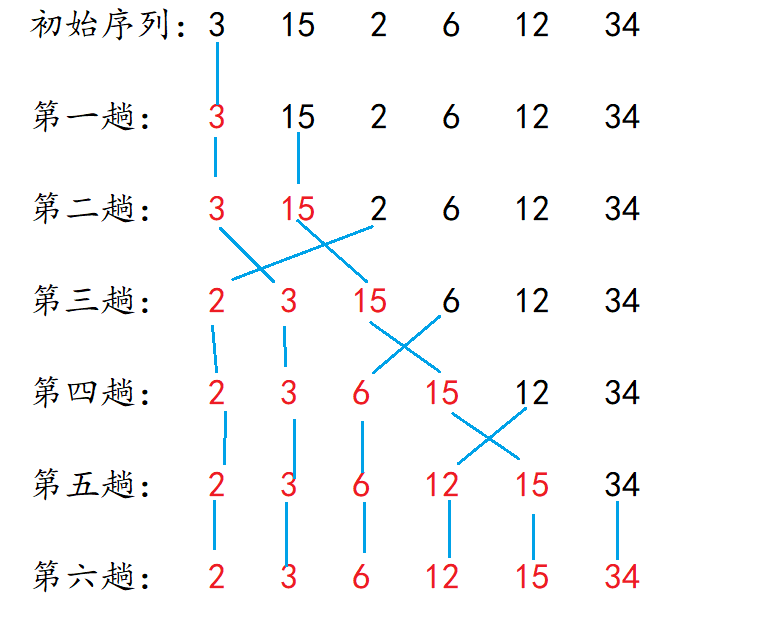
Basic idea of insertion sort
Sequences are divided into ordered and disordered.
In the initial state, the first number of the sequence is ordered. The first value of the disordered sequence is compared with the value of the ordered sequence from back to front, and the value is orderly inserted into the ordered sequence, so that the original ordered sequence becomes an ordered sequence with length plus one.
Code design
Define I and j, I controls the last element of the ordered sequence, j = i + 1, j is the first value of the unordered sequence (that is, the value to be compared). J (element [J]) is compared with the previous number element [J - 1]. If it is less than the previous element, J --; Continue the comparison if it is greater than the previous element. Stop the comparison. i++; The length of the ordered sequence plus one.
If the previous element of J element [ j-1 ] If the subscript j - 1 < 0, the element is compared with all elements and is the smallest element in the current ordered sequence. i++;
code implementation
public static<T extends Comparable<T>> void insertSort(T[] element){
if(element == null||element.length == 1){
return;
}
for(int i = 0;i< element.length;i++){
int j;
if(i == element.length -1){
j = i;
}else{
j = i+1;
}
for(;j>0;j--){
if(element[j] .compareTo(element[j-1])<0){
swap(element,j,j-1);
}else{
break;
}
}
}
}
private static <T> void swap (T[] element,int index1,int index2){
T temp = element[index1];
element[index1] = element[index2];
element[index2] = temp;
}
public static void main(String[] args) {
Integer[] arr = new Integer[]{1,4,6,3,2,7};
insertSort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+" ");
}
}Time and space complexity
Space complexity: O(1) No new memory space was opened up
Average time complexity: O(N^2)
Optimal time complexity: O(N) When the sequence is an ordered sequence, for example 1 2 3 4 5